Что такое интервал в математике

Интервал в математике – это участок числовой прямой, состоящий из всех чисел, находящихся между двумя заданными значениями. Узнайте, как определить интервал и какие его виды существуют в математике.

Интервал — это одно из основных понятий в математике, широко используемое в алгебре и анализе. Он представляет собой участок числовой прямой, включающий все числа, находящиеся между двумя заданными значениями. Интервалы часто используются для описания неопределенностей и неизвестных значений в математических моделях и уравнениях.

В математике существует несколько видов интервалов, которые отличаются своими характеристиками и правилами использования. Односторонние интервалы имеют только одну границу и включают все числа, большие (или меньшие) этой границы. Двусторонние интервалы имеют две границы и включают все числа, находящиеся между этими границами. Замкнутые интервалы включают границы, а открытые интервалы — нет. Полуоткрытые интервалы включают одну из границ, но не включают другую.

Примеры интервалов:

— Односторонний интервал: (5, +∞) — все числа, большие 5;

— Двусторонний интервал: [-2, 2] — все числа, находящиеся между -2 и 2, включая сами границы;

— Замкнутый интервал: [0, 1] — все числа от 0 до 1 включительно;

— Открытый интервал: (1, 3) — все числа между 1 и 3, не включая сами границы.

Интервалы являются важным инструментом в математическом анализе и различных областях науки, где требуется рассматривать непрерывные значения и величины. Они используются для решения уравнений, описания функций, моделирования физических процессов и других задач. Понимание и умение работать с интервалами поможет вам существенно расширить возможности и глубину вашего математического анализа.

Что такое интервал в математике?

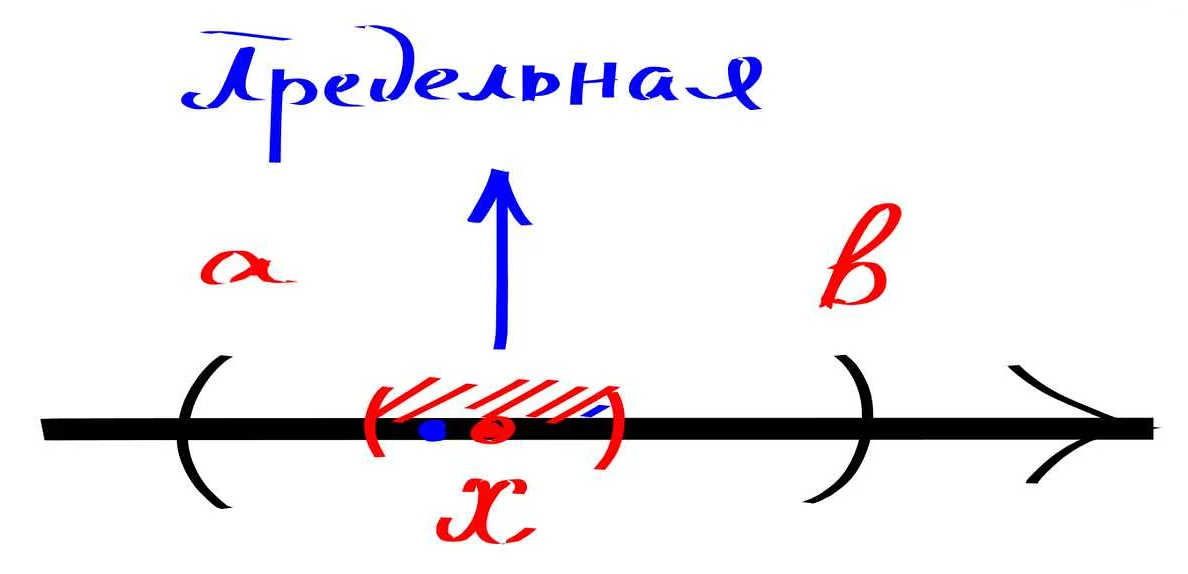
В математике выделяют следующие виды интервалов:

• Открытый интервал — это интервал, который не включает свои границы. Например, интервал (a, b), где a и b — числа, не включает сами a и b.
• Закрытый интервал — это интервал, который включает свои границы. Например, интервал [a, b], где a и b — числа, включает сами a и b.
• Полуоткрытый интервал — это интервал, который включает одну из своих границ. Например, интервал [a, b) включает a, но не включает b.
• Полузакрытый интервал — это интервал, который включает одну из своих границ. Например, интервал (a, b] не включает a, но включает b.

Интервалы широко используются в математике для описания непрерывных отрезков числовой прямой. Они также применяются в различных областях науки, техники и экономики для задания диапазонов значений и условий.

Открытый и закрытый интервалы

В математике интервалом называется множество всех чисел, находящихся между двумя заданными числами. В зависимости от того, включаются ли конечные точки в интервал, он может быть открытым или закрытым.

Открытый интервал обозначается символами (a, b) и включает в себя все числа, которые больше числа a и меньше числа b. При этом числа a и b не включаются в интервал. Например, интервал (3, 7) содержит все числа, которые больше 3 и меньше 7.

Закрытый интервал обозначается символами [a, b] и включает в себя все числа, которые больше или равны числу a и меньше или равны числу b. В отличие от открытого интервала, в закрытый интервал включаются конечные точки. Например, интервал [2, 5] содержит все числа, которые больше или равны 2 и меньше или равны 5.

Открытый и закрытый интервалы являются основными типами интервалов в математике и широко используются при решении задач и проведении исследований.

Односторонний и двусторонний интервалы

Интервалы в математике могут быть как односторонними, так и двусторонними. Односторонний интервал включает в себя только числа, меньшие или большие определенного значения, в то время как двусторонний интервал включает в себя числа, находящиеся между двумя определенными значениями.

Односторонний интервал может быть открытым или закрытым. В открытом одностороннем интервале одно из его концов не включается в интервал. Например, интервал (3, ∞) — это открытый односторонний интервал, который включает все числа, большие 3, но не включает само число 3. В закрытом одностороннем интервале оба конца включаются в интервал. Например, интервал [0, 5) — это закрытый односторонний интервал, который включает все числа от 0 до 5, не включая само число 5.

Двусторонний интервал состоит из двух конечных точек и включает все числа между этими точками. Например, интервал (1, 4) — это двусторонний интервал, который включает все числа между 1 и 4, не включая сами эти числа.

Односторонние и двусторонние интервалы широко применяются в математике при решении уравнений и неравенств, а также при обозначении диапазона значений в различных областях науки и естественных науках.

Бесконечные интервалы

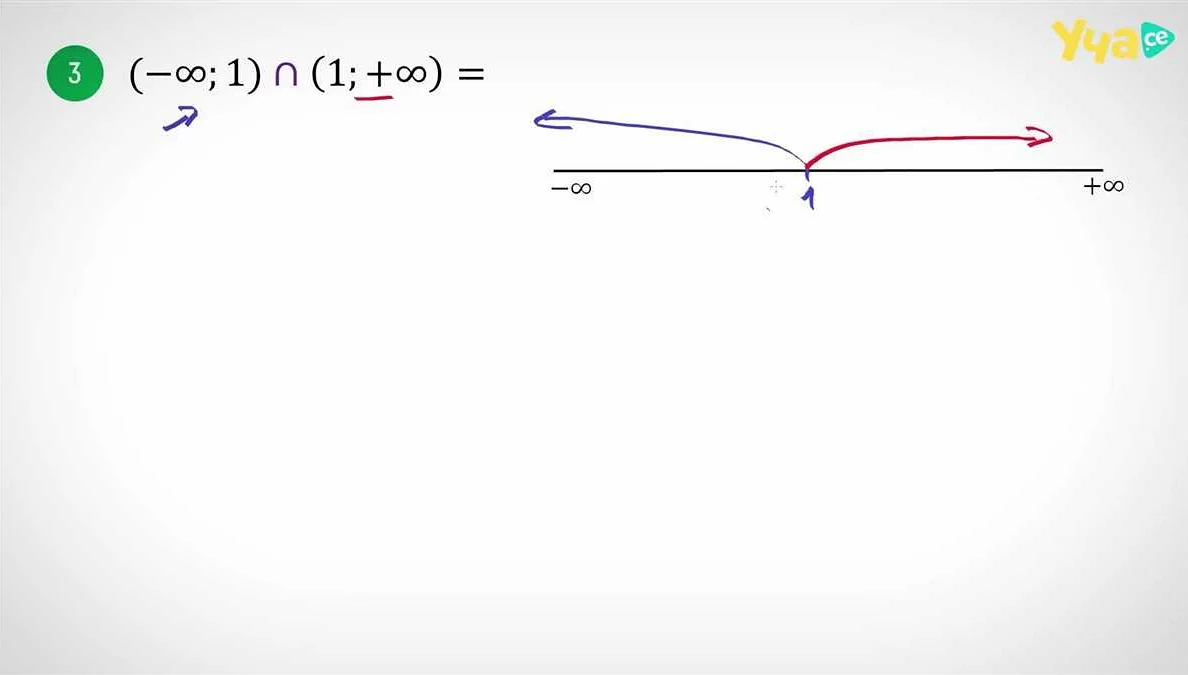
В математике существуют интервалы, которые не имеют конечных границ и распространяются бесконечно в одном или двух направлениях. Такие интервалы называются бесконечными интервалами.

Бесконечные интервалы могут быть полуоткрытыми или открытыми. Полуоткрытый бесконечный интервал имеет одну из границ, которая является бесконечностью, а другая граница является конечной. Например, интервал (-∞, 5) является полуоткрытым бесконечным интервалом, так как он начинается с минус бесконечности и заканчивается на числе 5.

Открытый бесконечный интервал не имеет ни одной конечной границы и простирается в обе стороны до бесконечности. Например, интервал (-∞, +∞) является открытым бесконечным интервалом.

Бесконечные интервалы встречаются в различных областях математики, таких как анализ, теория вероятности и теория множеств. Они играют важную роль при решении задач, связанных с пределами и бесконечностями.

Интервалы с десятичной точкой

Примеры интервалов с десятичной точкой:

• Интервал (1.5, 3.2) — это интервал, который содержит все числа от 1.5 до 3.2, не включая граничные значения.
• Интервал [0.2, 1.8] — это интервал, который содержит все числа от 0.2 до 1.8, включая граничные значения.
• Интервал (-∞, 4.7) — это интервал, который содержит все числа меньше 4.7.
• Интервал [2.3, +∞) — это интервал, который содержит все числа больше или равные 2.3.

Интервалы с десятичной точкой могут быть использованы для представления непрерывных значения, таких как время, температура, длина и т. д. Они могут быть полезны при решении задач в математике, физике, экономике и других областях.

Пустой интервал

Пустой интервал не имеет ни начальной, ни конечной точки. Все числа, которые могли бы входить в такой интервал, отсутствуют. Он является частным случаем интервала и не имеет никакого значения в математике.

Например, если мы рассматриваем интервал (1, 2), то в него входят все числа, большие 1 и меньшие 2. Однако, если мы рассматриваем интервал (2, 2), то этот интервал является пустым, так как число 2 не может быть одновременно больше и меньше самого себя.

Пустой интервал может возникнуть как результат математических операций, например, вычитания, при котором все числа из одного интервала исключаются из другого интервала, и в результате получается пустой интервал.

Пустой интервал не имеет физического смысла и не используется в практических расчетах. Однако, он является важным понятием в математике и может применяться в теоретических рассуждениях и доказательствах.

Примеры интервалов

В математике интервалы могут быть представлены различными способами. Рассмотрим несколько примеров интервалов:

1. Закрытый интервал:
   Интервал, который включает в себя все числа между двумя заданными числами и самые крайние числа интервала также включены. Обозначается с помощью квадратных скобок.

   Пример: [2, 7] — интервал, который содержит все числа от 2 до 7 включительно.

2. Открытый интервал:
   Интервал, который включает в себя все числа между двумя заданными числами, но самые крайние числа интервала не включены. Обозначается с помощью круглых скобок.

   Пример: (0, 1) — интервал, который содержит все числа больше 0 и меньше 1.

3. Полуоткрытый интервал:
   Интервал, который включает в себя все числа между двумя заданными числами, одно из крайних чисел включено, а другое не включено. Обозначается с помощью квадратной и круглой скобок.

   Пример: [0, 5) — интервал, который содержит все числа от 0 до 5, включая 0, но не включая 5.

Это лишь некоторые примеры интервалов, которые встречаются в математике. В зависимости от конкретной задачи и условий могут использоваться и другие виды интервалов.

Выводы

Виды интервалов:

Вид интервалаОпределениеПример

Открытый интервал	Интервал, который не включает крайние значения	(3, 7) — все числа, которые больше 3 и меньше 7
Закрытый интервал	Интервал, который включает крайние значения	[3, 7] — все числа, которые больше или равны 3 и меньше или равны 7
Полуоткрытый интервал	Интервал, который включает одно из крайних значений, но не включает другое	(3, 7] — все числа, которые больше 3 и меньше или равны 7

Интервалы в математике широко используются для описания непрерывных диапазонов значений и задания условий для переменных и функций.

Вопрос-ответ:

Что такое интервал в математике?

Интервал в математике – это множество всех чисел, которые находятся между двумя заданными числами или границами интервала.

Какие бывают виды интервалов?

В математике существуют четыре основных вида интервалов: открытый интервал, закрытый интервал, полуоткрытый интервал и бесконечный интервал.

Что такое открытый интервал?

Открытый интервал – это интервал, включающий все числа, которые больше первой границы и меньше второй границы интервала. Границы интервала не включаются в него сами.

Какой пример открытого интервала?

Примером открытого интервала может служить интервал (-5, 5), который включает все числа больше -5 и меньше 5, но не включает сами -5 и 5.

Что такое бесконечный интервал?

Бесконечный интервал – это интервал, который не имеет границы на одном или обоих концах. Например, интервал (-∞, 3) включает все числа, меньшие 3, а интервал (5, +∞) включает все числа, большие 5.

Видео по теме: