Что обозначает в математике в и на

В математике в и на используются для обозначения различных отношений и операций. В общем случае, ‘в’ относится к принадлежности элемента к множеству, а ‘на’ обозначает операции над множествами или объектами. Узнайте подробности о различных контекстах использования ‘в’ и ‘на’ в математике и как они влияют на решение задач и формулировку теорем.

В математике термины «в» и «на» играют важную роль при описании отношений и связей между объектами. Они используются для указания нахождения одного объекта внутри или на поверхности другого объекта. Правильное понимание этих терминов является фундаментом для понимания различных математических концепций.

Когда мы говорим, что один объект находится «в» другом объекте, мы подразумеваем, что первый объект находится внутри второго объекта. Например, если у нас есть шар и коробка, мы можем сказать, что шар находится «в» коробке. Это означает, что шар находится внутри пространства, ограниченного коробкой.

С другой стороны, когда мы говорим, что один объект находится «на» другом объекте, мы имеем в виду, что первый объект находится на поверхности второго объекта. Например, если мы говорим, что книга лежит «на» столе, мы подразумеваем, что книга находится на верхней поверхности стола.

Важно отметить, что термины «в» и «на» в математике могут быть использованы в различных контекстах и иметь разные значения в зависимости от ситуации. Поэтому при изучении новых математических понятий необходимо учитывать контекст и их специфическое использование.

Определение понятий «в» и «на» в математике

В математике термины «в» и «на» используются для указания отношения объектов друг к другу или к определенному пространству.

Когда говорят «в» математике, это означает, что объект находится внутри или содержится внутри другого объекта или определенной области. Например, если говорят «точка А находится внутри круга В», это означает, что точка А находится внутри границы круга В.

С другой стороны, когда говорят «на» математике, это означает, что объект находится на поверхности или границе другого объекта или определенной области. Например, если говорят «точка А находится на границе треугольника В», это означает, что точка А расположена на одной из сторон треугольника В.

Таким образом, использование терминов «в» и «на» в математике помогает четко определить положение объектов относительно друг друга или к определенному пространству, что является важным аспектом в изучении математических концепций и задач.

Значение предлога «в» в математике

Предлог «в» в математике используется для указания множества, в котором находятся элементы или объекты.

Например, рассмотрим уравнение «x входит в множество натуральных чисел». В таком случае «в» указывает на то, что рассматриваемый элемент x принадлежит множеству натуральных чисел.

Также предлог «в» используется при определении интервалов. Например, «x принадлежит интервалу (a, b)» означает, что значение x находится между a и b, но не включает их.

В математических выражениях предлог «в» может быть использован для указания области определения функции. Например, «f(x) = x^2, x в R» означает, что функция f(x) определена для всех значений x из множества действительных чисел.

Таким образом, предлог «в» в математике играет важную роль в указании множеств, интервалов и областей определения, что позволяет более точно определять и решать математические задачи.

Примеры использования предлога «в»

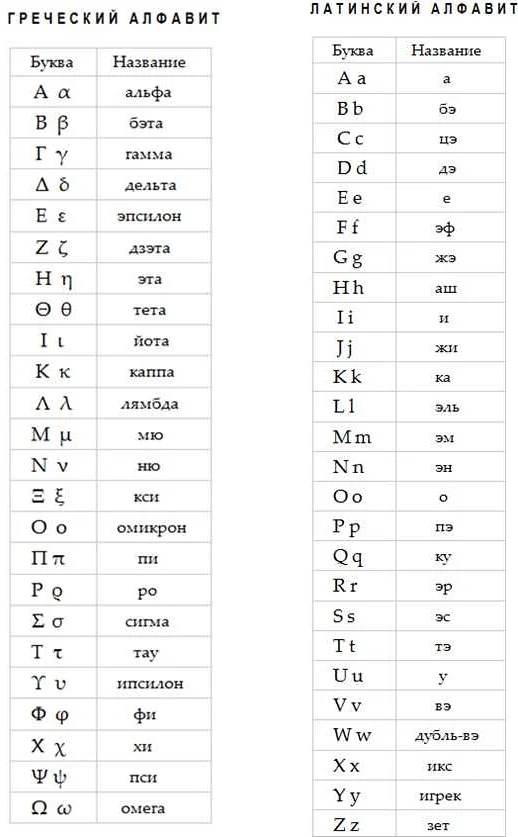
Предлог «в» широко используется в математике для обозначения множества, в котором находятся элементы или объекты.

Например, в алгебре множества могут быть обозначены следующим образом:

1. Вещественные числа в промежутке: [a, b], где a и b — граничные значения промежутка.

Пример: множество всех вещественных чисел от 0 до 1 включительно можно обозначить как [0, 1].

2. Множество точек в пространстве: В = {(x, y, z) | x, y, z — вещественные числа}.

Пример: множество всех точек в трехмерном пространстве можно обозначить как В.

3. Множество чисел в заданном диапазоне: В = {x | a ≤ x ≤ b}, где a и b — граничные значения диапазона.

Пример: множество всех чисел от 1 до 10 включительно можно обозначить как В = {x | 1 ≤ x ≤ 10}.

Также, предлог «в» может использоваться для обозначения включения одного множества в другое:

4. Множество А включено в множество В: A ⊆ B.

Пример: если множество А содержит элементы {1, 2, 3}, а множество В содержит элементы {1, 2, 3, 4, 5}, то можно сказать, что A ⊆ B.

Важно помнить, что контекст использования предлога «в» в математике может меняться в зависимости от конкретной задачи или области математики.

Значение предлога «на» в математике

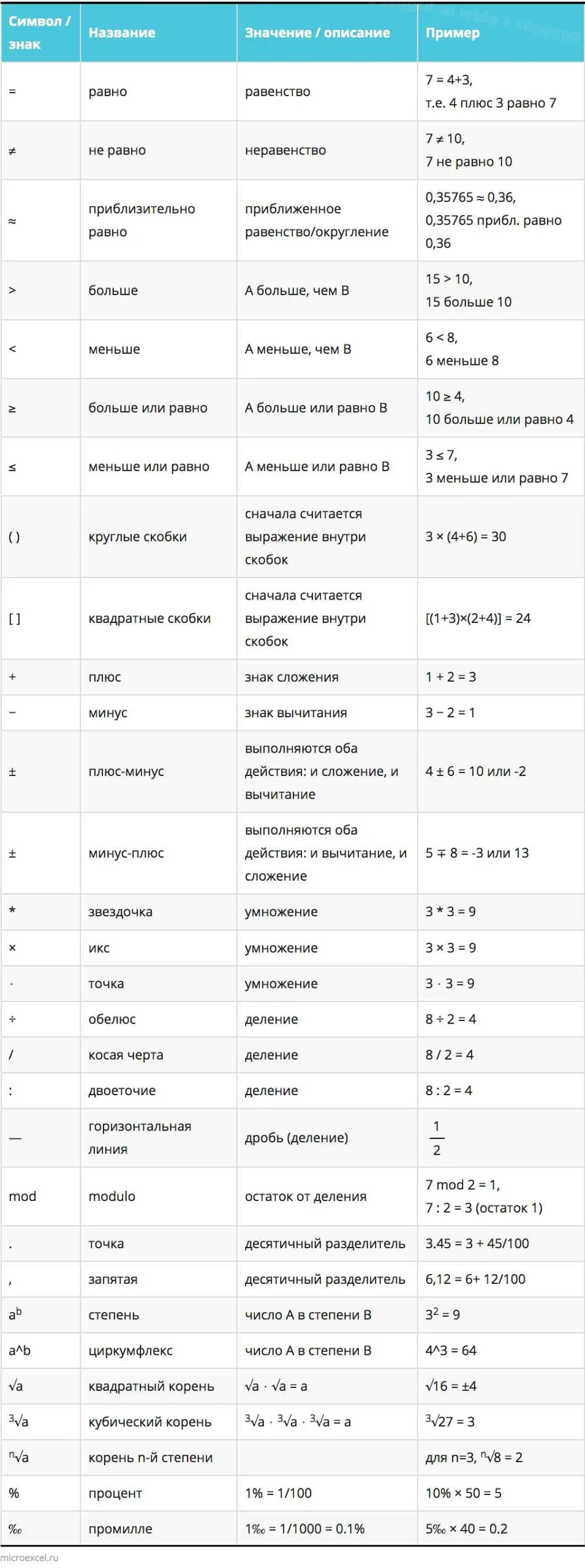
В математике предлог «на» может использоваться для обозначения различных отношений и операций. Рассмотрим несколько примеров:

ПримерЗначение

a + b = c	Сложение: значение переменной a прибавляется к значению переменной b и результат записывается в переменную c.
a — b = c	Вычитание: значение переменной b вычитается из значения переменной a и результат записывается в переменную c.
a * b = c	Умножение: значение переменной a умножается на значение переменной b и результат записывается в переменную c.
a / b = c	Деление: значение переменной a делится на значение переменной b и результат записывается в переменную c.
a % b = c	Остаток от деления: результатом операции будет остаток от деления значения переменной a на значение переменной b, записанный в переменную c.

Это лишь некоторые примеры использования предлога «на» в математике. В зависимости от контекста и предмета изучения, его значение может меняться и принимать различные интерпретации.

Примеры использования предлога «на»

Предлог «на» в математике может использоваться в разных контекстах. Он может обозначать разные отношения и операции.

Вот несколько примеров использования предлога «на» в математике:

ПримерОбозначениеОписание

2 + 3 = 5	+	Операция сложения: на 2 прибавить 3 равно 5.
7 — 4 = 3	—	Операция вычитания: из 7 вычесть 4 равно 3.
5 × 2 = 10	×	Операция умножения: 5 умножить на 2 равно 10.
8 ÷ 4 = 2	÷	Операция деления: 8 разделить на 4 равно 2.
a = b	=	Равенство: переменная a равна переменной b.
x < y	<	Меньше: переменная x меньше переменной y.
x > y	>	Больше: переменная x больше переменной y.

Это лишь некоторые примеры использования предлога «на» в математике. В зависимости от контекста, он может иметь и другие значения и обозначения.

Разница между предлогами «в» и «на» в математике

В математике предлоги «в» и «на» употребляются для описания разных отношений и значений.

Предлог «в» используется, когда мы говорим о том, что что-то находится внутри определенного пространства или множества. Например, в математических выражениях, мы можем сказать, что число находится внутри определенного диапазона значений, например: «x в диапазоне от 1 до 10». Это означает, что значение переменной «x» может принимать любое число от 1 до 10 включительно.

Предлог «на» используется, когда мы говорим о том, что что-то находится на поверхности или на плоскости. Например, в геометрии мы можем сказать, что точка находится на прямой или на плоскости. Также, в математических выражениях, мы можем говорить о значении функции на определенной точке, например: «f на точке x равно 5». Это означает, что значение функции «f» в точке «x» равно 5.

Таким образом, разница между предлогами «в» и «на» в математике заключается в отношении между объектом и пространством или поверхностью, на которой он находится.

Предлог «в»Предлог «на»

В диапазоне от 1 до 10	На плоскости
Внутри множества	На прямой
В матрице	На графике

Вопрос-ответ:

Что означает «в» и «на» в математике?

В математике «в» и «на» используются для указания положения объекта относительно другого объекта или множества.

Какие примеры можно привести для понимания использования «в» и «на» в математике?

Например, говорят «точка на прямой» или «точка в плоскости» — это указывает на положение точки относительно прямой или плоскости.

Каково значение «в» и «на» в контексте графов и диаграмм?

В графах и диаграммах «в» указывает на принадлежность элемента к множеству, например, «вершина в графе», а «на» используется для указания положения элемента на графе, например, «ребро на графе».

Какие примеры можно привести для использования «в» и «на» в математических операциях?

Например, говорят «число в квадрате» или «число на степень» — это указывает на операцию возведения числа в квадрат или в степень.

Каково значение «в» и «на» в математических формулах?

В математических формулах «в» и «на» используются для указания принадлежности элемента к множеству или операции с элементами, например, «x в множестве действительных чисел» или «x на поле комплексных чисел».

Видео по теме: