Что обозначает на и в в математике

В математике на и в обозначают операции объединения и пересечения множеств соответственно. На операции объединения объединяют два или более множества, в результате получается новое множество, содержащее все элементы исходных множеств. В операции пересечения находятся общие элементы двух или более множеств, и результатом является новое множество, содержащее только эти общие элементы. Знаки на и в являются важными в математической нотации и используются для обозначения различных операций.

В математике существуют различные символы и обозначения, которые помогают нам описывать и понимать различные математические концепции. Два из таких символов — «на» и «в» — часто используются для обозначения отношений и принадлежности.

Символ «на» обычно используется для обозначения отношений между двумя элементами: один элемент находится «на» другом. Например, в математическом выражении «a на b» символ «на» указывает, что элемент «a» находится на элементе «b». Это может означать, что «a» является подмножеством «b» или что «a» является составной частью «b».

Символ «в» часто используется для обозначения принадлежности элемента к множеству или группе. Например, в математическом выражении «x в A» символ «в» указывает, что элемент «x» принадлежит множеству «A». Это означает, что «x» является одним из элементов множества «A» и может быть использован в операциях и вычислениях, связанных с этим множеством.

Примеры использования символов «на» и «в» в математике могут быть разнообразными. Например, в геометрии, мы можем сказать, что точка «A» находится на прямой «BC», обозначая это как «A на BC». А в алгебре, мы можем сказать, что число «5» принадлежит множеству натуральных чисел, обозначая это как «5 в N».

Таким образом, символы «на» и «в» играют важную роль в математике, помогая нам описывать и понимать отношения и принадлежность между элементами и множествами.

Определение математических обозначений «на» и «в»

Обозначение «на» обычно используется для указания, что один объект является частью другого или лежит на поверхности другого объекта. Например, если говорят «точка A на отрезке BC», то это означает, что точка A принадлежит отрезку BC или лежит на его поверхности.

Обозначение «в» чаще всего используется для указания, что один объект находится внутри другого объекта. Например, если говорят «точка A внутри треугольника ABC», то это означает, что точка A находится внутри треугольника ABC, а не на его границе.

Примеры:

1. Точка A на прямой AB.

2. Точка B на окружности O.

3. Точка C внутри квадрата ABCD.

4. Точка D внутри окружности O.

Определение понятия «на» в математике

В математике понятие «на» часто используется для обозначения отношения одного объекта или значения к другому. Оно может иметь различные значения в зависимости от контекста.

Во-первых, «на» может указывать на рассмотрение объекта или значения на поверхности другого объекта или внутри него. Например, говоря о точке на прямой, мы имеем в виду, что эта точка находится на поверхности прямой. А если говорим о числе на интервале, то имеем в виду, что это число находится внутри данного интервала.

Во-вторых, «на» может означать принадлежность объекта или значения к множеству или классу. Например, говоря о числе на множестве натуральных чисел, мы имеем в виду, что это число является элементом данного множества.

Кроме того, «на» может использоваться для обозначения действий, которые выполняются на объекте или значении. Например, говоря о функции на множестве, мы имеем в виду, что эта функция определена на данном множестве и принимает значения из него.

И наконец, «на» может указывать на зависимость одного объекта или значения от другого. Например, говоря о функции на промежутке, мы имеем в виду, что значения функции зависят от значений на этом промежутке.

Таким образом, понятие «на» в математике имеет различные значения и используется для обозначения отношений и свойств объектов и значений.

Примеры использования обозначения «на» в математике

Обозначение «на» в математике часто используется для указания отношения или операции, которая выполняется с одним объектом или числом относительно другого. Вот несколько примеров использования обозначения «на» в математике:

1. Деление одного числа на другое: например, выражение 10 на 2 обозначает деление числа 10 на число 2, что дает результат 5.
2. Умножение числа на другое: например, выражение 5 на 3 обозначает умножение числа 5 на число 3, что дает результат 15.
3. Возведение числа в степень: например, выражение 2 на 3 обозначает возведение числа 2 в третью степень, что дает результат 8.
4. Процентное соотношение: например, выражение 25% на 100 обозначает 25 процентов от числа 100, что дает результат 25.
5. Математические отношения: например, выражение a на b обозначает отношение числа a к числу b.

Это лишь несколько примеров использования обозначения «на» в математике. Важно помнить, что в каждом конкретном случае значение обозначения «на» может зависеть от контекста и специфики проблемы или задачи.

Определение понятия «в» в математике

Если элемент находится в множестве, то он может быть рассмотрен как одно из его составляющих. Например, если рассмотреть множество целых чисел {1, 2, 3}, то число 2 находится в данном множестве, так как оно является его элементом. Мы можем записать это как «2 входит в множество {1, 2, 3}» или «2 ∈ {1, 2, 3}».

Оператор «в» используется в различных математических конструкциях, таких как уравнения, неравенства, множества и т.д. Он помогает определить, какие элементы принадлежат множеству или удовлетворяют заданному условию.

ПримерЗначение

2 ∈ {1, 2, 3}	Истина, так как число 2 является элементом множества {1, 2, 3}
5 ∈ {1, 2, 3}	Ложь, так как число 5 не является элементом множества {1, 2, 3}
x ∈ {x | x > 0}	Истина, если переменная x больше нуля

Таким образом, понятие «в» в математике обозначает принадлежность элемента к множеству или удовлетворение условию.

Примеры использования обозначения «в» в математике

Обозначение «в» в математике часто используется для указания принадлежности элемента множеству. Например, если имеется множество A = {1, 2, 3}, то можно записать выражение «1 в A», что означает, что элемент 1 принадлежит множеству A.

Также обозначение «в» может использоваться для указания принадлежности точки к геометрическому объекту. Например, если имеется окружность с центром в точке O и радиусом r, то можно записать выражение «точка P в окружности O», что означает, что точка P принадлежит данной окружности.

В некоторых случаях обозначение «в» может использоваться для указания включения одного объекта в другой. Например, если имеется отрезок AB и отрезок BC, то можно записать выражение «отрезок AB включает отрезок BC», что означает, что отрезок BC полностью содержится внутри отрезка AB.

В общем случае обозначение «в» используется для указания принадлежности или включения одного объекта в другой и может применяться в различных математических областях.

Сходства и различия между «на» и «в» в математике

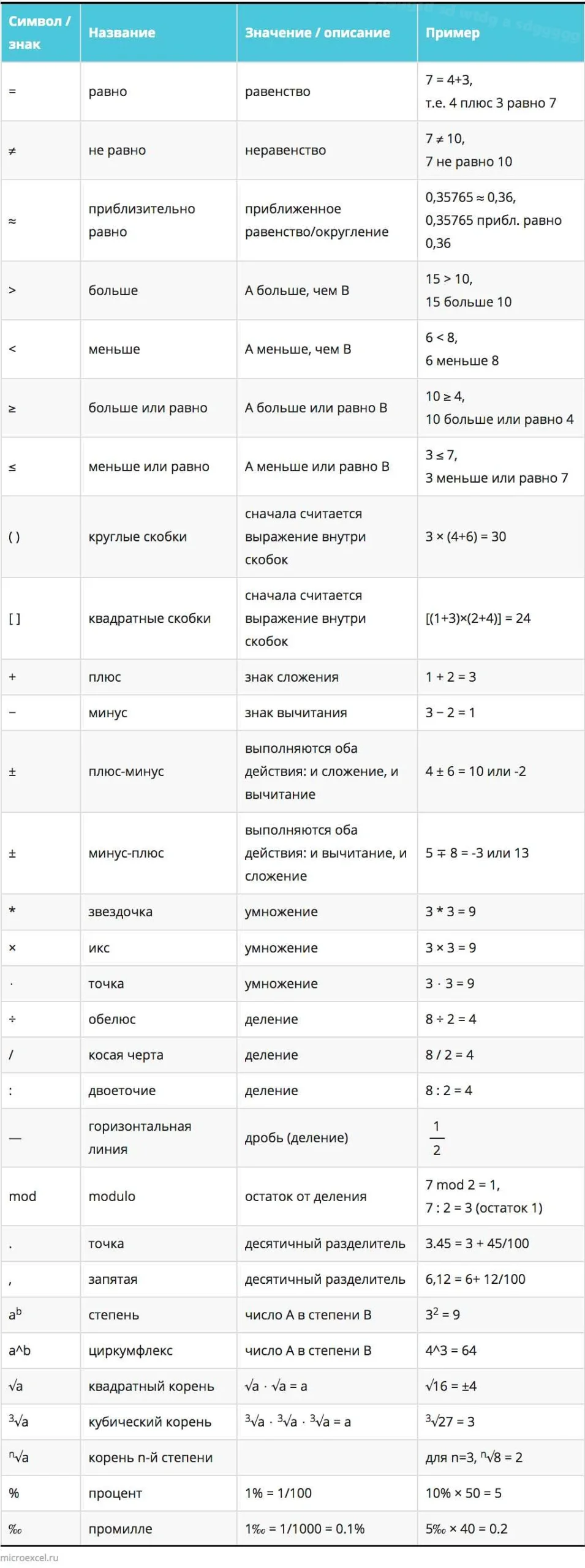
В математике предлоги «на» и «в» используются для указания основного пространства, в котором происходят операции или действия.

Оба предлога могут обозначать размещение объекта или числа в определенном множестве или совокупности. Например, можно сказать «число на числовой оси» или «точка в координатной плоскости». В обоих случаях «на» и «в» указывают на место нахождения объекта в определенной структуре.

Однако, есть и некоторые различия в использовании этих предлогов. Предлог «на» чаще всего используется для указания точного местоположения объекта на поверхности или в пределах некоторого пространства. Например, «точка на графике функции» или «число на числовой прямой».

С другой стороны, предлог «в» обычно используется для указания объекта, находящегося внутри некоторого множества или структуры. Например, «точка внутри круга» или «число в интервале от 1 до 10». В этих случаях «в» указывает на принадлежность объекта к определенной области или интервалу значений.

Таким образом, сходство между предлогами «на» и «в» заключается в том, что они оба указывают на место нахождения объекта в некотором пространстве. Однако, различия между ними заключаются в том, что «на» обозначает точное местоположение, а «в» указывает на принадлежность объекта к определенной структуре или области.

Видео по теме:

Вопрос-ответ:

Что обозначает «на» и «в» в математике?

В математике символ «на» используется для обозначения отношений между числами, а символ «в» используется для обозначения множества, в котором находятся элементы.

Какие примеры использования символа «на» в математике?

Примеры использования символа «на» в математике: a на b означает, что a делится на b без остатка; a на b делится с остатком; a на b равно c; a на b больше c и так далее.

Какие примеры использования символа «в» в математике?

Примеры использования символа «в» в математике: a в B означает, что a является элементом множества B; a входит в B; a принадлежит B; a принадлежит интервалу (a, b) и так далее.

Какие еще существуют символы для обозначения отношений в математике, кроме «на» и «в»?

Помимо символов «на» и «в», в математике используются также символы «=», «≠», «>», »

Можно ли использовать символы «на» и «в» вместе в одном выражении?

Да, можно использовать символы «на» и «в» вместе в одном выражении. Например, a на b в интервале (c, d) означает, что a делится на b без остатка и a принадлежит интервалу (c, d).

Какие значения имеют предлоги «на» и «в» в математике?

В математике, предлоги «на» и «в» могут использоваться для обозначения различных понятий. В контексте графов и таблиц, «на» может означать принадлежность элемента к множеству или группе, а «в» может обозначать включение элемента в множество. В контексте координатной плоскости, «на» может означать принадлежность точки к определенному множеству, а «в» может означать вхождение точки в определенную область или фигуру.

Особые случаи использования «на» и «в» в математике

На может обозначать:

1. Отношение между двумя математическими объектами, когда один объект находится на поверхности или внутри другого объекта. Например, «точка А на отрезке В» или «окружность на плоскости».
2. Условие или ограничение, которое должно выполняться для определенного математического объекта. Например, «функция на заданном интервале», «матрица на нулевом столбце» и т.д.

В может обозначать:

1. Отношение между двумя математическими объектами, когда один объект находится внутри другого объекта. Например, «точка А внутри окружности В» или «треугольник В внутри квадрата С».
2. Предел или предел по некоторому параметру. Например, «сумма ряда в пределе» или «функция в точке сходится».

Примеры:

• Точка М на линии АВ.
• Окружность С на плоскости XYZ.
• Функция f(x) на интервале [a, b].
• Треугольник А внутри круга В.
• Сумма ряда в пределе.

Влияние правильного использования обозначений «на» и «в» на решение математических задач

Правильное использование обозначений «на» и «в» в математике имеет большое влияние на решение различных математических задач. Корректное понимание и применение этих обозначений позволяет более точно и ясно формулировать задачу, а также более точно интерпретировать результаты.

Обозначение «на» в математике обычно используется для указания принадлежности или отношения между объектами. Например, «x находится на оси координат» означает, что значение переменной x соответствует определенной точке на оси координат. Также, «множество A находится на множестве B» означает, что все элементы множества A являются частью множества B.

Обозначение «в» в математике обычно используется для указания содержания или вхождения одного объекта в другой. Например, «x находится в интервале (a, b)» означает, что значение переменной x лежит между значениями a и b. Также, «множество A входит в множество B» означает, что все элементы множества A также являются элементами множества B.

Правильное использование обозначений «на» и «в» позволяет избежать путаницы и недоразумений при формулировке и решении математических задач. Например, при решении задачи на поиск максимума функции, правильное определение области, на которой функция определена, с использованием обозначения «на», позволяет избежать неправильного результата. Точное понимание, что функция определена на интервале (a, b), а не в интервале [a, b], может существенно изменить решение задачи.

Поэтому, важно уделить должное внимание правильному использованию обозначений «на» и «в» в математике, чтобы быть уверенным в точности результатов и предотвратить возможные ошибки при решении математических задач.