Что такое 1 а в математике

Что такое 1 а в математике? Узнайте об этом в нашей статье. Мы рассмотрим определение, свойства и примеры использования числа 1 а в математических выражениях и уравнениях.

Когда мы говорим о числе «1 а» в математике, мы обычно имеем в виду рациональное число, которое можно представить в виде одной целой части и одной десятичной части, разделенных точкой. Например, число 1.5 может быть записано как «1 а». Такое представление чисел удобно использовать при работе с дробями и процентами, а также при решении задач из области финансов и экономики.

Число 1 а также может использоваться для обозначения десятых и сотых частей целого числа. Например, число 0.01 можно записать как «1 а» и прочитать как «одна сотая». А число 0.5 будет выглядеть как «5 а» и читаться как «пять десятых». Такое представление позволяет нам точно указать долю целого числа, что часто бывает полезно в реальных ситуациях.

Примеры использования числа 1 а: 1.5 а (одна целая пять десятых), 0.25 а (две целых пятьдесят сотых), 2.75 а (две целых семьдесят пять сотых).

Таким образом, понятие «1 а» в математике помогает нам более точно описывать и работать с дробными числами, а также имеет множество практических применений в нашей повседневной жизни.

а в математике: понятие и примеры

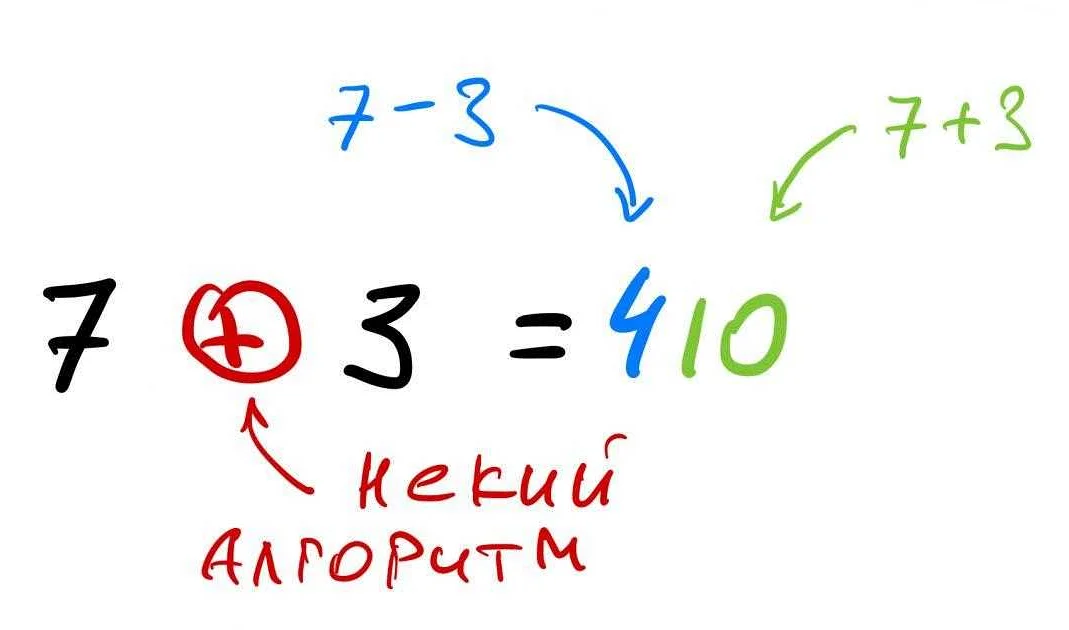
В математике, «а» обозначает переменную или неизвестное значение. Она используется для представления числа, которое мы не знаем или которое может изменяться в зависимости от контекста.

Пример 1:

• Уравнение «а + 5 = 10» означает, что значение «а» должно быть таким, чтобы прибавление 5 давало результат 10. В этом случае значение «а» равно 5.
• Уравнение «3а — 7 = 2» означает, что значение «а» должно быть таким, чтобы умножение на 3 и вычитание 7 давали результат 2. В этом случае значение «а» равно 3.

Пример 2:

1. Если «а» представляет собой количество яблок, то уравнение «а + 3 = 7» означает, что нужно найти количество яблок, чтобы прибавление 3 давало результат 7. В этом случае значение «а» равно 4.
2. Если «а» представляет собой возраст человека, то уравнение «2а — 10 = 30» означает, что нужно найти возраст, чтобы умножение на 2 и вычитание 10 давали результат 30. В этом случае значение «а» равно 20.

Таким образом, переменная «а» в математике используется для представления неизвестного значения или переменной в уравнениях и задачах.

Видео по теме:

Определение и особенности числа 1 а

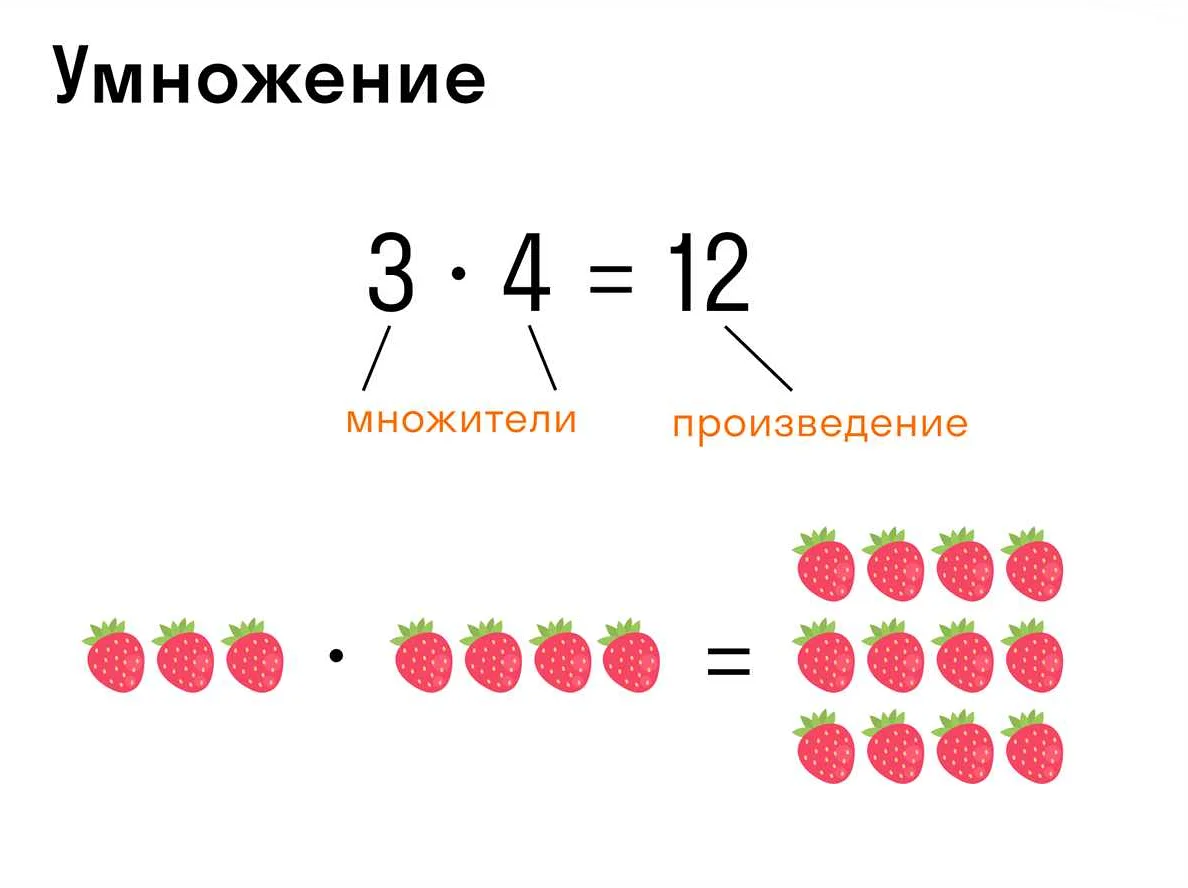
Основная особенность числа 1 а заключается в том, что оно является наименьшим натуральным числом. Это значит, что перед числом 1 а нет других натуральных чисел. Оно является начальным элементом натурального ряда и служит базой для построения всех остальных чисел.

Также стоит отметить, что число 1 а является нейтральным элементом относительно умножения. Это означает, что умножение числа на 1 а не изменяет его значения. Например, 5 умноженное на 1 а равно 5. Эта особенность используется во многих математических операциях и свойствах чисел.

В математике число 1 а также играет важную роль во многих областях. Оно используется для обозначения единичной длины, времени, массы и других физических и геометрических величин. Также число 1 а является основой для определения других чисел, таких как десятичные и дробные числа.

В заключение, число 1 а является основой для всей математики и играет важную роль в различных областях. Оно является начальным элементом натурального ряда и обладает особыми свойствами, которые делают его уникальным.

Свойства и характеристики числа 1 а

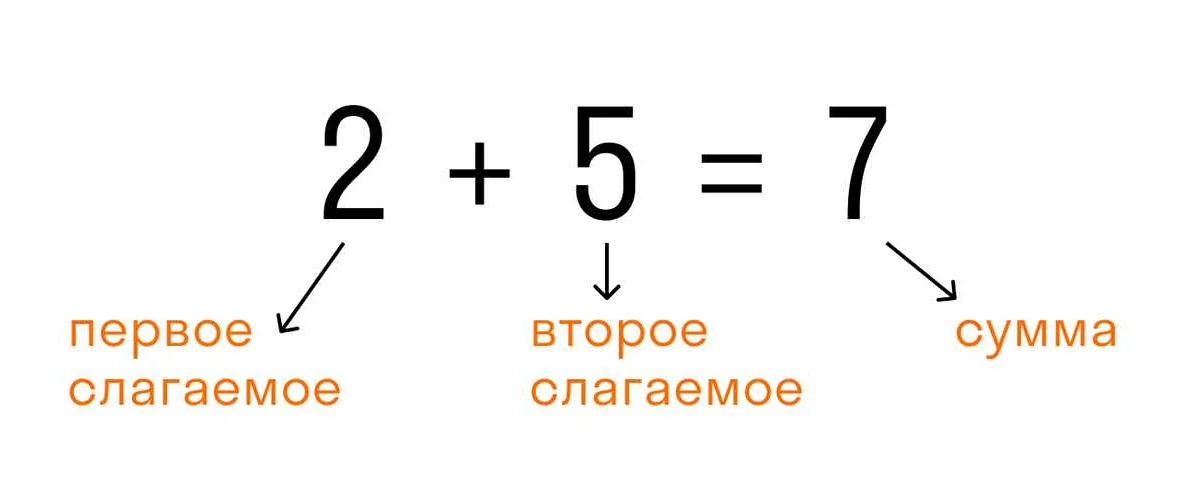
• 1 а является натуральным числом и является первым числом в натуральном ряду.
• 1 а является нейтральным элементом относительно умножения: любое число, умноженное на 1 а, равно этому числу.
• 1 а является нейтральным элементом относительно сложения: любое число, прибавленное к 1 а, равно этому числу.
• 1 а возводится в любую степень и остается равным 1 а.
• 1 а является делителем любого числа, кроме 0.
• Произведение 1 а на любое число равно этому числу.
• 1 а является единственным числом, не имеющим делителей, кроме 1 и самого себя.

Таким образом, число 1 а является уникальным и важным элементом в математике, обладающим рядом особых свойств и характеристик.

Как использовать число 1 а в вычислениях

Число 1 а в математике представляет собой число, состоящее из единицы, после которого следует неопределенное количество нулей. Это число имеет особую роль в вычислениях и может быть использовано в различных ситуациях.

Одним из основных применений числа 1 а является его использование в качестве масштаба или коэффициента. Например, если у нас есть некоторое значение, и мы хотим увеличить его в 10 раз, мы можем просто умножить это значение на число 1 а. Таким образом, если у нас есть число 5, умноженное на 1 а, мы получим число 50.

Кроме того, число 1 а может использоваться для округления чисел. Например, если у нас есть число 3.1415926535897932384626433, и мы хотим округлить его до двух десятичных знаков, мы можем умножить это число на 1 а в степени -2. В результате получим число 3.14.

Также число 1 а может быть использовано для представления очень больших или очень маленьких чисел. Например, если у нас есть число 1 а в степени 100, это будет представлять число 1, с последующими 100 нулями. Такое число очень большое и не может быть записано в обычном виде.

В заключение, число 1 а является важным инструментом в математике и может быть использовано в различных вычислениях. Оно позволяет масштабировать значения, округлять числа и представлять очень большие или очень маленькие числа.

Примеры вычислений с числом 1 а

Число 1 а (единица а) используется в математике для обозначения неопределенности или произвольности величины.

Пример 1: Рассмотрим уравнение 1 а + 3 = 7. Чтобы найти значение переменной а, нужно из обеих частей уравнения вычесть число 3, чтобы оставить а в одной части: 1 а = 4. Таким образом, значение переменной а равно 4.

Пример 2: Рассмотрим выражение 2 + 1 а. Здесь неопределенная величина а может принимать различные значения. Например, если а равно 3, то выражение будет равно 2 + 3 = 5. Если же а равно -2, то выражение будет равно 2 + (-2) = 0.

Пример 3: Рассмотрим уравнение 3 * 1 а = 15. Чтобы найти значение переменной а, нужно разделить обе части уравнения на число 3: 1 а = 5. Таким образом, значение переменной а равно 5.

Пример 4: Рассмотрим выражение 1 а — 5. Здесь неопределенная величина а может принимать различные значения. Например, если а равно 8, то выражение будет равно 8 — 5 = 3. Если же а равно 2, то выражение будет равно 2 — 5 = -3.

Таким образом, использование числа 1 а в математике позволяет работать с неизвестными или произвольными величинами и находить их значения в выражениях и уравнениях.

Сравнение числа 1 а с другими числами

Сравнивая число 1 а с другими числами, можно сказать, что оно больше нуля и меньше двух. Также оно меньше любого положительного целого числа и больше любого отрицательного целого числа.

Число 1 а можно сравнивать с другими иррациональными числами, например, с числом π (пи). Оба числа являются иррациональными и не повторяющимися десятичными дробями, но их точные значения различны.

ЧислоСравнение с числом 1 а

0	Меньше
1	Меньше
1/2	Меньше
2	Больше
π	Различается

Таким образом, число 1 а обладает своими особыми свойствами и можно сравнивать его с другими числами, чтобы определить их взаимное положение.

Примеры задач, в которых используется число 1 а

1. Первый пример задачи:

У Маши было 5 яблок. Она съела 2 яблока. Сколько яблок осталось у Маши?

Решение:

• У Маши было 5 яблок.
• Она съела 2 яблока.
• Чтобы найти количество яблок, которые остались у Маши, вычитаем количество съеденных яблок из первоначального количества.
• 5 — 2 = 3
• У Маши осталось 3 яблока.

2. Второй пример задачи:

В классе было 30 учеников. 10 учеников пропустили занятия. Сколько учеников пришло на занятие?

Решение:

• В классе было 30 учеников.
• 10 учеников пропустили занятия.
• Чтобы найти количество учеников, которые пришли на занятие, вычитаем количество пропустивших из первоначального количества.
• 30 — 10 = 20
• На занятие пришло 20 учеников.

3. Третий пример задачи:

У Пети было 12 марок. Он отдал 1 марку своему другу. Сколько марок осталось у Пети?

Решение:

• У Пети было 12 марок.
• Он отдал 1 марку своему другу.
• Чтобы найти количество марок, которые осталось у Пети, вычитаем количество отданных марок из первоначального количества.
• 12 — 1 = 11
• У Пети осталось 11 марок.

Это лишь некоторые примеры задач, в которых используется число 1 а. В математике оно часто используется для обозначения количества или изменений количества. Оно позволяет нам решать разнообразные задачи и делать различные вычисления.

Практическое применение числа 1 а в разных областях

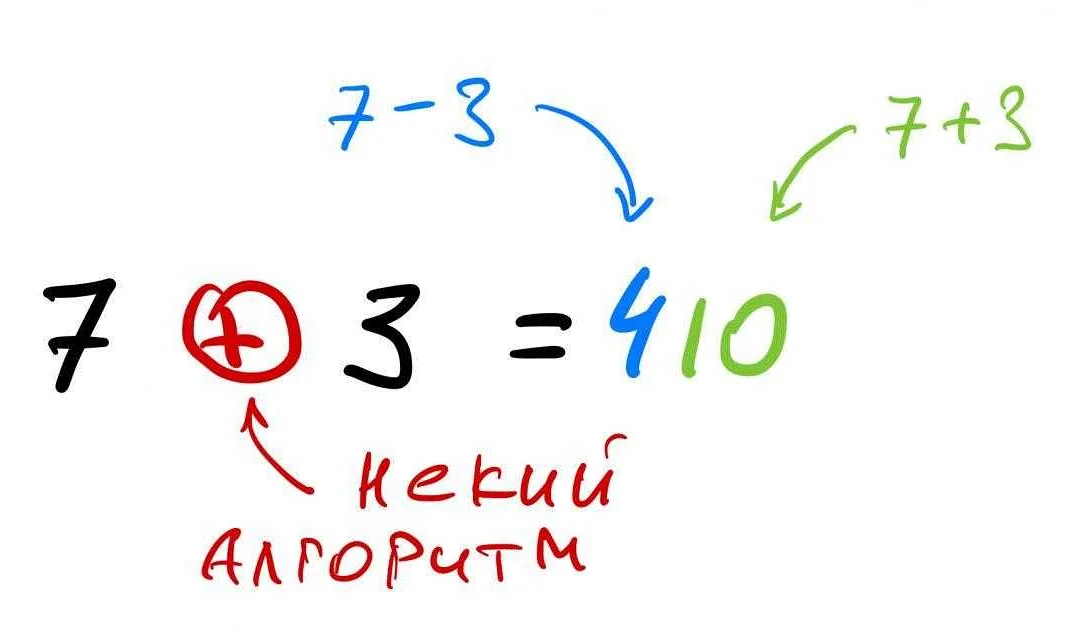
В физике число 1 а применяется для описания изменения величин во времени. Оно используется в уравнении экспоненциального роста и десятичных логарифмов. Также оно находит применение в теории вероятности и статистике, где используется для описания вероятности событий.

В экономике число 1 а применяется для моделирования и прогнозирования экономических процессов. Оно используется в формулах для расчета процентных ставок, инфляции и других финансовых показателей. Также оно находит применение в оптимизационных задачах, где используется для поиска максимальной или минимальной значения функции.

В компьютерных науках число 1 а используется для описания битовых операций и логических вычислений. Оно также играет важную роль в алгоритмах и программировании, где используется для определения начальных условий и циклов выполнения.

В медицине число 1 а применяется для расчетов доз лекарств и концентрации веществ в организме. Оно также используется для описания вероятности заболевания и эффективности лечения. В биологии число 1 а применяется для моделирования генетических процессов и эволюции организмов.

В практической жизни число 1 а применяется для измерения времени, длины, площади и других физических величин. Оно используется в различных формулах и уравнениях для решения задач различной сложности.

Таким образом, число 1 а имеет широкое практическое применение в различных областях и играет важную роль в решении различных задач. Оно является одним из основных математических и научных констант и неотъемлемой частью современной науки и технологий.

Вопрос-ответ:

Что такое 1 а в математике?

1 а в математике — это единица измерения площади, равная площади квадрата со стороной длиной 1 аршин.

Какие единицы измерения можно использовать вместо 1 а в математике?

Вместо 1 а в математике можно использовать другие единицы измерения площади, такие как квадратные метры, квадратные сантиметры или квадратные дюймы.

Как рассчитать площадь в 1 а?

Для расчета площади в 1 а нужно умножить длину стороны квадрата в аршинах на саму себя. Например, если сторона квадрата равна 5 аршинам, то площадь будет равна 5 а * 5 а = 25 а^2.

Какую площадь занимает 1 а в метрической системе измерений?

1 а в метрической системе измерений занимает площадь, равную 100 квадратным метрам. То есть, 1 а = 100 м^2.

Как можно использовать 1 а в повседневной жизни?

1 а можно использовать для измерения площади небольших участков земли, например, в саду или огороде. Также, 1 а может быть полезен при планировании строительства или ремонта, чтобы оценить объем материалов, необходимых для покрытия площади.

Что означает 1 а в математике?

1 а в математике обозначает единицу в алгебре. Это число, которое используется для обозначения единицы в различных математических операциях и выражениях.

Какие примеры использования 1 а в математике?

Примеры использования 1 а в математике включают запись чисел, например, 10 а означает 10 единиц или 111 а означает 111 единиц. Также 1 а может быть использовано в алгебре, например, в выражении 2 а + 3 означает 2 единицы, умноженные на а, плюс 3.