Определение и примеры смешаных чисел в математике для учеников 5 класса
Содержимое
- 1 Определение и примеры смешаных чисел в математике для учеников 5 класса
Смешанное число в математике 5 класс — это число, представленное смесью целой части и десятичной дроби. Узнайте, как представлять смешанные числа, как их складывать, вычитать и умножать, а также в каких ситуациях использовать смешанные числа.
Смешанное число — это числовое значение, которое состоит из целой части и обыкновенной дроби. Для понимания смешанного числа необходимо знать, что дробь — это часть целого числа, представленная в виде отношения числителя и знаменателя.
В математике 5 класса смешанные числа часто используются для представления нецелых величин, таких как длительность времени, расстояние или количество предметов. Смешанное число позволяет точно указать, сколько целых единиц и долей составляют данную величину.
Смешанное число записывается в виде целая часть + дробная часть. Например, если имеется число 3 и 1/2, то его смешанная запись будет выглядеть как 3 1/2. В этом случае 3 — это целая часть, а 1/2 — дробная часть.
Важно уметь правильно выполнять операции с смешанными числами. Например, для сложения или вычитания смешанных чисел необходимо сложить или вычесть их целые части отдельно, а затем сложить или вычесть их дробные части. При умножении или делении смешанных чисел также нужно учитывать их целые и дробные части.
Смешанное число в математике
Смешанное число в математике представляет собой комбинацию целой части и дробной части числа. Оно может быть записано в виде целого числа, за которым следует дробь, например, 3 1/2.
В смешаных числах целая часть указывает на количество полных единиц, а дробная часть показывает часть, меньшую единицы. Например, в числе 3 1/2 целая часть равна 3, а дробная часть равна 1/2, что означает половину единицы.
Смешанные числа могут быть положительными или отрицательными, в зависимости от значения их целой части. Например, смешанное число -2 3/4 будет отрицательным, так как целая часть равна -2.
Смешанные числа могут использоваться для представления нецелых значений, таких как дробные числа или результаты деления. Они могут быть полезны при решении задач, связанных с долями, объемами, временем и др.
Для выполнения операций с смешанными числами, их части могут быть преобразованы в обычные десятичные дроби или числители и знаменатели дробей могут быть сложены, вычтены, умножены или разделены отдельно.
Знание смешанных чисел поможет учащимся более полно понимать и использовать разнообразные математические концепции и решать задачи, связанные с дробями и десятичными числами.
Определение смешанного числа

Например, число 3 1/2 является смешанным числом. Здесь целая часть равна 3, а дробная часть равна 1/2.
Смешанное число можно представить в виде обыкновенной дроби. Для этого нужно умножить целую часть на знаменатель дроби и прибавить числитель дроби. Полученное число станет числителем новой обыкновенной дроби, а знаменатель останется прежним.
Например, смешанное число 3 1/2 можно представить в виде обыкновенной дроби следующим образом: 3 1/2 = (3 * 2 + 1) / 2 = 7/2.
Смешанные числа часто используются для записи нецелых чисел, которые удобно представить в виде целой части и дробной части.
Как записать смешанное число
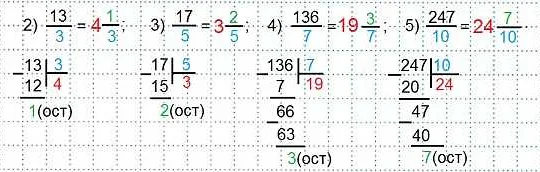
Смешанное число состоит из целой части и дробной части, которые записываются отдельно. Для записи смешанного числа используется следующий формат:
Целая частьДробная частьСмешанное число
| Цифра или цифры, обозначающие количество целых единиц | Десятичная дробь, записанная отдельно | Целая часть + дробная часть |
Например, для записи числа 3 целых единиц и 1/4, сначала записываем целую часть — 3, а затем дробную часть — 1/4. Смешанное число будет выглядеть так: 3 1/4.
Важно помнить, что при записи смешанного числа между целой и дробной частями ставится пробел.
Примеры смешанных чисел
Смешанные числа представляют собой числа, которые состоят из целой части и дробной части. Дробная часть записывается после целой части и разделяется знаком дроби.
Примеры смешанных чисел:
1. 21/2 — это число, которое имеет целую часть 2 и дробную часть 1/2.
2. 33/4 — это число, которое имеет целую часть 3 и дробную часть 3/4.
3. 42/3 — это число, которое имеет целую часть 4 и дробную часть 2/3.
4. 55/6 — это число, которое имеет целую часть 5 и дробную часть 5/6.
5. 61/4 — это число, которое имеет целую часть 6 и дробную часть 1/4.
Таким образом, смешанные числа являются числами, состоящими из целой части и дробной части, разделенных знаком дроби.
Сложение смешанных чисел

Процесс сложения смешанных чисел можно представить следующим образом:
- Сложение целых частей чисел. Если у чисел разные знаки, то вычитаем модули целых частей и определяем знак результата.
- Сложение дробных частей чисел. Дробные части чисел складываются обычным образом.
- Если после сложения дробных частей получается неправильная дробь, её можно преобразовать в смешанное число.
Например, чтобы сложить смешанные числа 2 1/2 и 1 3/4, нужно сложить целые части (2 + 1 = 3) и дробные части (1/2 + 3/4 = 5/4). Получаем результат 3 5/4. Если нужно, эту дробь можно преобразовать в смешанное число (3 1/4).
Таким образом, сложение смешанных чисел не отличается от сложения обыкновенных чисел, но требует дополнительных шагов для сложения целых и дробных частей.
Вычитание смешанных чисел
Чтобы выполнить вычитание смешанных чисел, необходимо выполнить следующие шаги:
- Вычислить разность между дробными частями смешанных чисел. Если дробная часть уменьшаемого числа больше дробной части вычитаемого числа, необходимо занять 1 из целой части уменьшаемого числа и увеличить его дробную часть на 1.
- Вычислить разность между целыми частями смешанных чисел. Если целая часть уменьшаемого числа меньше целой части вычитаемого числа, необходимо занять 1 из целой части следующего числа и увеличить его дробную часть на 1.
- Полученные разности объединить в одно смешанное число. Если разность дробных частей отрицательная, необходимо занять 1 из целой части полученного числа и увеличить его дробную часть на 1.
Пример:
Дано:
- Уменьшаемое число: 4 3/4
- Вычитаемое число: 1 1/2
Шаг 1: Вычислим разность между дробными частями:
- 3/4 — 1/2 = 1/4
Шаг 2: Вычислим разность между целыми частями:
- 4 — 1 = 3
Шаг 3: Объединим полученные разности:
- Разность: 3 1/4
Ответ: 3 1/4
Умножение смешанных чисел

Смешанное число представляет собой комбинацию целой части и десятичной дроби. Умножение смешанных чисел осуществляется следующим образом:
1. Преобразуем смешанное число в неправильную дробь. Для этого умножаем целую часть на знаменатель и складываем полученное значение с числителем. Результат записываем в виде дроби, где числитель — сумма числителя дроби и произведения целой части на знаменатель, а знаменатель остается прежним.
2. Умножаем числитель первой дроби на числитель второй дроби и записываем результат в числитель итоговой дроби.
3. Умножаем знаменатель первой дроби на знаменатель второй дроби и записываем результат в знаменатель итоговой дроби.
4. Сокращаем полученную дробь, если это возможно.
5. Если итоговая дробь имеет отрицательное значение, меняем знак числителя на противоположный.
6. В случае необходимости преобразуем неправильную дробь в смешанное число. Для этого делим числитель на знаменатель. Целая часть полученного значения становится целой частью смешанного числа, а остаток — новой дробной частью.
Таким образом, умножение смешанных чисел сводится к умножению обыкновенных дробей и последующему преобразованию полученной дроби.
Деление смешанных чисел

Смешанные числа представляют собой комбинацию целой части и дробной части. При выполнении операции деления смешанных чисел необходимо привести их к общему знаменателю и затем разделить числитель.
Процесс деления смешанных чисел можно разбить на несколько шагов:
Шаг 1: Приведение смешанных чисел к общему знаменателю. Для этого необходимо умножить целую часть на знаменатель и прибавить к результату дробную часть. Например, при делении 3 1/2 на 2 1/3 необходимо привести числа к общему знаменателю 6, умножив 3 на 6 и прибавив 1/2, а также умножив 2 на 6 и прибавив 1/3, получив 19/6 и 13/3 соответственно.
Шаг 2: Деление числителя нового смешанного числа на числитель другого смешанного числа. В нашем примере, мы делим 19/6 на 13/3. Для этого необходимо умножить числитель первого числа на обратное значение числителя второго числа. То есть, умножаем 19 на 3 и делим на 6, получая результат 19/2.
Шаг 3: Приведение результата к смешанному числу. В нашем примере, 19/2 можно представить как 9 1/2.
Таким образом, деление смешанных чисел требует приведения чисел к общему знаменателю, деления числителя и приведения результата к смешанному числу.
Вопрос-ответ:
Что такое смешанное число?
Смешанное число — это число, которое состоит из целой части и дробной части, разделенных знаком «или». Например, 2 1/2 или 3 3/4.
Как записывается смешанное число?
Смешанное число записывается в виде целой части, пробела, дробной части, где числитель дробной части меньше знаменателя, разделенных знаком «или». Например, 2 1/2 или 3 3/4.
Как смешанное число преобразуется в неправильную дробь?
Чтобы преобразовать смешанное число в неправильную дробь, нужно умножить целую часть на знаменатель дроби и прибавить числитель дробной части. Результат станет числителем, знаменатель останется прежним. Например, смешанное число 2 1/2 преобразуется в неправильную дробь 5/2.
Как смешанное число преобразуется в правильную дробь?
Чтобы преобразовать смешанное число в правильную дробь, нужно умножить целую часть на знаменатель дроби, прибавить числитель дробной части и это будет новый числитель. Знаменатель остается прежним. Например, смешанное число 3 3/4 преобразуется в правильную дробь 15/4.
Как можно складывать и вычитать смешанные числа?
Для сложения или вычитания смешанных чисел нужно сложить (или вычесть) целые части отдельно и дробные части отдельно. Если дробные части имеют одинаковые знаменатели, то их можно сложить (или вычесть) и результат оставить с тем же знаменателем. Если дробные части имеют разные знаменатели, нужно привести их к общему знаменателю, а затем сложить (или вычесть). Например, 2 1/2 + 3 3/4 = 5 5/4.
Что такое смешанное число?
Смешанное число — это число, которое состоит из целой части и дробной части, разделенных дробной чертой. Например, 3 1/2 или 4 3/4.



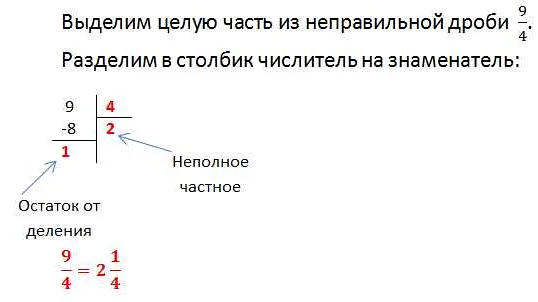

Смешанное число в математике 5 класса — это число, которое состоит из целой части и дробной части. Например, такое число, как 3 ½, является смешанным числом. Целая часть числа указывает, сколько целых единиц содержится в числе, а дробная часть показывает, какую часть от целой единицы оно представляет. Смешанное число можно представить в виде обыкновенной дроби, например, число 3 ½ можно записать как 7/2. Также смешаное число можно представить в виде десятичной дроби, например, 3 ½ можно записать как 3.5. Смешанные числа широко используются в повседневной жизни, например, при измерениях и в финансовых расчетах. Они позволяют нам точно указывать количество целых единиц и часть от них. Понимание смешанных чисел важно для развития математических навыков и позволяет легче работать с дробями и переводить их из одной формы в другую.
Спасибо за полезную статью! Я, как родитель, всегда стараюсь быть в курсе учебной программы своего ребенка, чтобы помочь ему в обучении. Ваше объяснение о смешанных числах в математике 5 класса было очень понятным и доступным. Теперь я понимаю, что смешанное число — это число, которое состоит из целой части и дробной части, например, 2 1/2. Я также узнал, что смешанное число можно представить в виде обыкновенной дроби, где целая часть — это целое число, а дробная часть — это обыкновенная дробь. Это очень полезное знание, которое поможет моему ребенку успешно справиться с заданиями по математике. Спасибо за вашу работу!
Статья очень понятно и доступно объясняет, что такое смешанное число в математике для учеников 5 класса. Она помогла мне разобраться в этой теме и осознать, что смешанное число состоит из целой части и дробной части, что является очень полезной информацией. Мне понравилось, как автор подошел к объяснению материала, используя примеры из повседневной жизни, что сделало его еще интереснее и понятнее. Теперь я уверена, что смешанные числа – это не так сложно, как казалось раньше. Большое спасибо за статью!