Что такое arch в математике

Arch в математике — это функция, которая показывает угол между двумя точками на окружности или эллипсе. Узнайте как использовать arch для измерения углов и нахождения расстояний на геометрических фигурах.

Arch (арка) — это понятие, которое активно используется в математике и имеет важное значение в различных областях этой науки, таких как геометрия, тригонометрия, анализ и другие. В данной статье мы рассмотрим основные определения arch и его применение в различных математических задачах.

В геометрии arch обычно относится к части окружности, которая ограничена двумя точками. Эти точки называются концами арки. Длина arch равна длине дуги между этими точками и измеряется в радианах или градусах. Одно из основных применений arch в геометрии — вычисление длины окружности и построение различных фигур на плоскости.

В тригонометрии arch определяет обратные функции тригонометрических функций, таких как sin, cos и tan. Например, arch sin x обозначает ту угловую меру, при которой синус этого угла равен x. Arch sin x возвращает значение в радианах и может быть использовано для вычисления углов в различных задачах, включая решение треугольников и построение графиков функций.

Arch также используется в анализе для определения обратной функции экспоненты. Функция arch(x) возвращает значение y, при котором e^y = x. Она широко применяется в решении дифференциальных уравнений, интегралов и других задач.

В заключение, arch играет важную роль в математике, предоставляя нам возможность работать с обратными функциями и решать различные задачи в геометрии, тригонометрии и анализе. Понимание основных определений и применения arch является ключевым для успешного изучения и применения математических концепций и методов.

Что такое arch в математике

Функция arcsinh(x), или обратная гиперболическому синусу, является такой функцией, которая удовлетворяет условию sinh(arcsinh(x)) = x. Она является монотонно возрастающей и неограниченной.

Функция arcsinh(x) имеет множество применений в математическом анализе и физике. Она используется в задачах, связанных с гармоническими колебаниями, распределением вероятностей, теории упругости и других областях.

Известно, что гиперболический синус sinh(x) и его обратная функция arcsinh(x) являются аналогами тригонометрических функций синуса и arcsin(x) соответственно. Вместе с гиперболическим косинусом и обратными функциями arch и arccos они составляют основу гиперболической тригонометрии, которая активно применяется в математике и физике.

Видео по теме:

Определение

В геометрии, арка — это часть окружности, ограниченная двумя точками. Арки могут быть полной (соответствует 360 градусам или 2π радианам) или частичной (любой угол меньше 360 градусов).

Термин «arch» также может относиться к различным математическим функциям или моделям, которые имеют форму арки. Например, дуга синусоиды или парабола могут быть названы «arch».

Arch также может использоваться для обозначения архимедового спирали, которая образуется при равномерной обмотке пространства вокруг оси, такой как спираль на раковине.

Термин «arch» имеет широкий спектр применений в различных областях математики, физики и инженерии. В архитектуре «arch» также может относиться к арочным конструкциям, которые используются для создания прочных и эстетически привлекательных зданий.

Арккосинус

Арккосинус возвращает угол, значение косинуса которого равно x. В отличие от косинуса, который принимает значения от -1 до 1, арккосинус определен для значений x от -1 до 1.

Значение арккосинуса измеряется в радианах и может быть от -π/2 до π/2. Оно определяет угол между осью Ox и лучом, исходящим из начала координат и проходящим через точку с координатами (1, x) на единичной окружности.

Применение арккосинуса в математике широко. Он используется для решения уравнений, нахождения углов в треугольниках и для определения длин сторон треугольника по заданным углам.

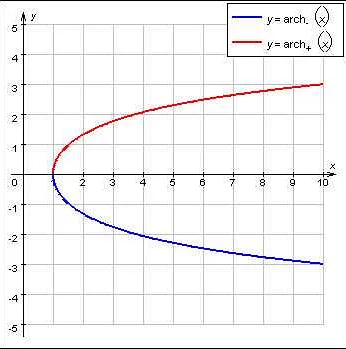
Арксинус

Значение арксинуса может быть в диапазоне от -π/2 до π/2 радиан (от -90° до 90°). Исключение составляет значение арксинуса для x = 1, которое равно π/2, а для x = -1 – -π/2.

Арксинус широко используется в тригонометрии, физике, инженерии и других областях, где необходимо решать уравнения, связанные с синусами.

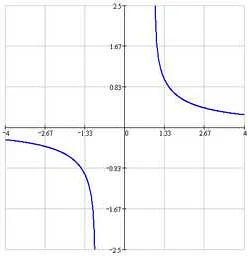
Арктангенс

Арктангенс – это угол, значение тангенса которого равно x. Иными словами, если tg(α) = x, то α = arctg(x).

Значения арктангенса лежат в интервале от -π/2 до π/2. Однако, в зависимости от области применения функции, значения могут быть ограничены или расширены.

Арктангенс является одной из основных тригонометрических функций и находит широкое применение в различных областях математики и физики. В тригонометрии используется для нахождения углов, а в анализе – для решения уравнений и задач, связанных с тангенсом.

Аргумент (x)Значение (arctg(x))

0	0
1	π/4
√3	π/3
∞	π/2

В таблице представлены некоторые значения арктангенса для различных аргументов.

Применение

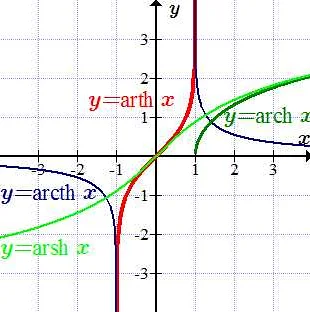
Понятие «arch» также используется в геометрии для определения арков, которые представляют собой часть окружности между двумя точками. Арки широко применяются в строительстве, дизайне и архитектуре для создания изящных форм и красивых переходов.

В компьютерной графике и визуализации понятие «arch» используется для создания плавных и естественных кривых. Алгоритмы, основанные на арках, позволяют создавать реалистичные изображения и анимацию.

Понятие «arch» также используется в теории вероятностей и статистике для определения архимедовой копулы, которая представляет собой функцию распределения для двумерного случайного вектора. Архимедовые копулы широко применяются в финансовой математике, экономике и других областях для моделирования зависимостей между случайными величинами.

Таким образом, понятие «arch» имеет множество применений в различных областях математики и наук, что делает его важным инструментом для исследования и решения различных задач.

Геометрия

Геометрия включает в себя такие понятия, как точка, линия, плоскость, угол, фигура и тело. С помощью этих понятий геометрия анализирует различные геометрические фигуры, исследует их свойства и взаимоотношения.

Геометрия находит широкое применение в различных областях, таких как архитектура, инженерия, физика, компьютерная графика и дизайн. Она помогает определить формы и размеры объектов, рассчитать площади и объемы, а также решить различные практические задачи.

Геометрия также имеет свои основные принципы и правила, которые позволяют строить доказательства и выводить новые теоремы. Одной из важных частей геометрии является аналитическая геометрия, которая использует методы алгебры для изучения геометрических объектов.

Важным понятием в геометрии является понятие прямой, которая является самой простой и наиболее фундаментальной фигурой. Прямая не имеет начала и конца и состоит из бесконечного числа точек.

Геометрия играет важную роль в нашей жизни, помогая нам понять и описать мир вокруг нас. Она позволяет нам анализировать и визуализировать данные, строить модели и прогнозы, а также решать различные задачи в научных и практических областях.

ФигураОписание

Треугольник	Фигура, состоящая из трех сторон и трех углов.
Прямоугольник	Фигура, у которой все углы прямые.
Круг	Фигура, все точки которой равноудалены от центра.

Тригонометрия

Основной объект изучения в тригонометрии – это треугольник. С помощью тригонометрических функций, таких как синус, косинус и тангенс, можно определить соотношения между углами и сторонами треугольников. Эти функции позволяют решать различные задачи, связанные с измерением и вычислением углов и расстояний.

Тригонометрия также имеет свои собственные формулы и тождества, которые позволяют упростить вычисления и решение уравнений. Некоторые известные тригонометрические тождества включают формулы сложения и вычитания синусов и косинусов, а также формулу двойного угла.

Применение тригонометрии широко распространено в различных областях. Например, в физике она используется для моделирования колебаний волн и движения тел. В астрономии тригонометрия позволяет измерять расстояния до звезд и планет. В инженерии и компьютерной графике тригонометрические функции применяются при создании трехмерных моделей и анимаций.

Физика

Физика описывает мир с помощью математических моделей, законов и теорий. Она изучает различные области, такие как механика, электричество и магнетизм, оптика, термодинамика, ядерная физика, квантовая механика и другие. Физика играет важную роль в различных научных и инженерных областях и используется для разработки новых технологий и улучшения существующих.

Важной задачей физики является поиск общих закономерностей и установление связей между различными явлениями, а также построение теорий, которые объясняют эти явления. Эксперименты и наблюдения играют решающую роль в развитии физики, так как они позволяют проверить и подтвердить или опровергнуть существующие теории и модели.

Физика имеет широкий спектр применений в нашей повседневной жизни и в различных областях, включая медицину, инженерию, информационные технологии и многие другие. Она помогает нам понять и объяснить феномены, такие как движение тел, электрические и магнитные явления, свет и звук, тепло и многое другое.

Вопрос-ответ:

Что такое арх в математике?

Арх в математике — это сокращение от архимедовой функции, которая используется для измерения углов в градусах, минутах и секундах.

Какие основные определения связаны с архом в математике?

Основные определения, связанные с архом в математике, включают в себя архимедову функцию, градус, минуту и секунду, которые используются для измерения углов.

Как применяются архи в математике?

Архи применяются в математике для измерения углов. Они используются в геометрии, тригонометрии и других разделах математики для описания и измерения угловых величин.

Можете привести примеры использования архов в математике?

Конечно! Примеры использования архов в математике включают измерение углов при построении графиков функций, решении задач геометрии, вычислении тригонометрических функций и т. д. Например, при решении задачи нахождения площади треугольника с помощью тригонометрии, мы можем использовать архи для измерения углов треугольника и вычисления синуса или косинуса этих углов.