Что такое бифуркация в математике

Бифуркация в математике — это понятие, которое описывает возникновение изменений в системе при изменении параметров. В данной статье мы рассмотрим основные типы бифуркаций и их применение в различных областях науки и техники.

Бифуркация — одно из важных понятий в математике, которое широко используется для анализа сложных динамических систем. Это особое состояние, когда при малых изменениях входных данных происходит качественное изменение в поведении системы. Бифуркация может привести к появлению новых структур, циклов, хаосу или стабильности системы.

Определение бифуркации часто связывается с понятием критического значения параметра. Когда параметр достигает этого значения, система переходит в новое состояние, что приводит к бифуркации. Такое изменение состояния может быть как резким, так и плавным, в зависимости от типа бифуркации.

Примером бифуркации является бифуркация Хопфа, когда при изменении параметра система переходит от устойчивого состояния к циклическому. Другим примером является бифуркация бифуркаций, когда система переходит от одного типа бифуркации к другому при изменении параметра. Такие сложные динамические системы можно встретить в различных областях, включая физику, биологию, экономику и др.

Понимание бифуркаций является важным для анализа и прогнозирования поведения систем. Они позволяют увидеть, как изменения входных данных могут повлиять на долгосрочное поведение системы, что может быть полезно при принятии решений или планировании. Изучение бифуркаций помогает понять фундаментальные принципы динамики и сложности, лежащие в основе многих явлений в природе и обществе.

Что такое бифуркация в математике?

Основная идея бифуркации заключается в том, что при небольшом изменении входных данных или параметров системы, ее поведение может резко измениться. Это может проявляться в изменении числа и структуры устойчивых решений, появлении новых режимов работы или даже внезапном переходе системы из одного состояния в другое. Бифуркация может быть качественной или количественной.

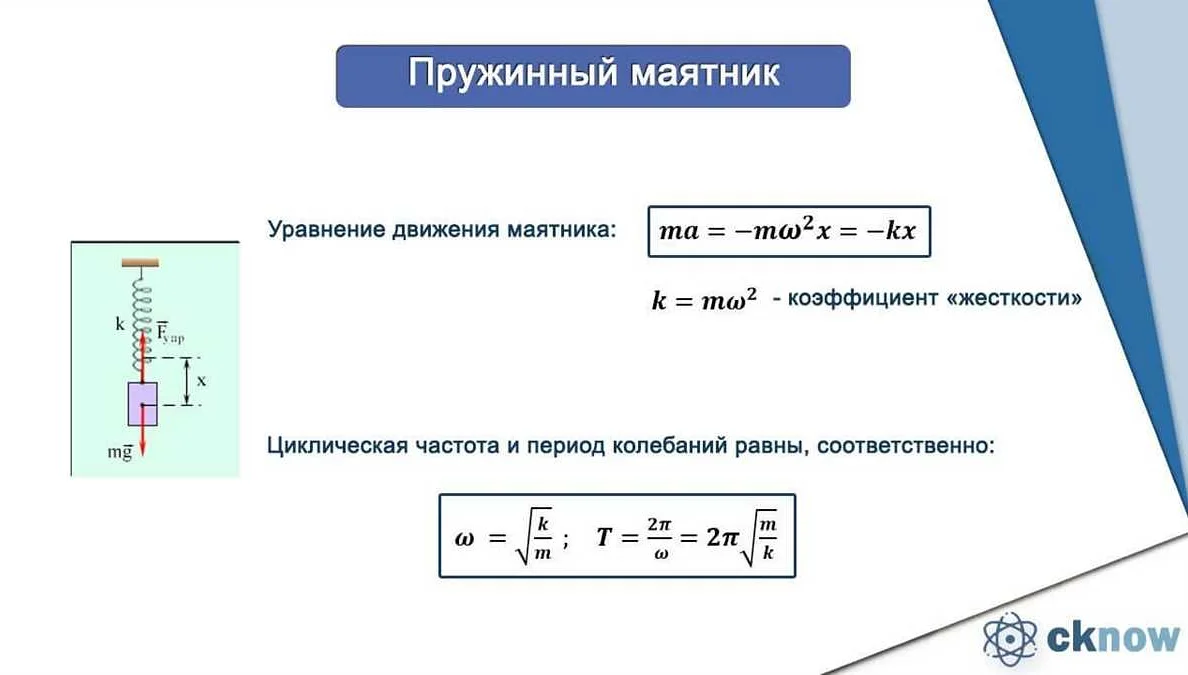
Примером бифуркации может служить система дифференциальных уравнений, описывающая движение математического маятника. При изменении параметров, например, длины подвеса или массы маятника, система может переходить из режима колебаний в режим вращения или наоборот. Это является примером бифуркации, где изменение параметров приводит к качественному изменению решений системы.

Изучение бифуркаций имеет большое значение в различных научных и инженерных областях, таких как физика, химия, биология, экономика и другие. Понимание бифуркаций помогает предсказывать и объяснять различные явления и процессы, происходящие в природе и в технических системах. Бифуркации также имеют практическое применение, например, в управлении сложными системами и создании инновационных технологий.

Примеры бифуркаций:Описание

Бифуркация Хопфа	Возникновение осцилляций и нейтральной устойчивости при изменении параметров
Бифуркация седла-узел	Переход системы из устойчивого состояния в неустойчивое при изменении параметров
Бифуркация Неймарка-Сакера	Появление сложных периодических решений при изменении параметров

Определение бифуркации в математике

Бифуркации выявляются при изучении динамических систем, которые описывают эволюцию во времени. Эти системы могут представлять собой физические процессы, биологические модели, экономические системы или другие явления, которые можно описать математически.

Основная идея бифуркации заключается в том, что небольшие изменения в параметрах системы могут привести к качественно различным результатам. В одних случаях система может оставаться стабильной и предсказуемой, в других — происходят резкие изменения, переходы или колебания.

Бифуркации имеют важное значение в различных областях науки, таких как физика, биология, экономика, климатология и др. Они позволяют понять и объяснить сложное поведение систем и предсказать возможные сценарии их развития.

Для изучения и анализа бифуркаций применяются различные методы и модели, включая численные методы, графические методы и теорию динамических систем. Исследование бифуркаций помогает увидеть особенности системы и предоставляет информацию о ее устойчивости, разнообразии состояний и возможных переходах между ними.

Примеры бифуркаций

1. Катастрофическая бифуркация

2. Суперкритическая бифуркация

3. Периодическая бифуркация

Примеры бифуркации

Примеры бифуркации в математике включают:

НазваниеОписание

Бифуркация седло-узел	При изменении параметра система может переходить от устойчивого узла к седлу, что приводит к изменению ее поведения.
Бифуркация бифуркационного узла	В этом случае две устойчивые точки сталкиваются и исчезают, что влияет на качественное поведение системы.
Бифуркация транскритического типа	При изменении параметра система может переходить от одного устойчивого состояния к другому, в результате чего происходит скачкообразное изменение поведения.
Бифуркация ветвления	В этом случае при изменении параметра система может непрерывно создавать новые устойчивые точки, что приводит к возникновению новых состояний и поведений.

Это только некоторые примеры бифуркации, и существует множество других видов бифуркаций, которые могут возникать в различных системах и моделях.

Значение бифуркации в математике

Бифуркация в математике представляет собой критическую точку, в которой происходит изменение структуры или поведения системы. Это важное понятие широко применяется в различных областях, включая дифференциальные уравнения, динамические системы и теорию хаоса.

Значение бифуркации заключается в том, что она помогает понять, как система может изменяться с течением времени или при изменении параметров. Бифуркации могут происходить, когда система достигает определенного порогового значения или при изменении внешних условий.

Примеры бифуркаций включают разветвление, когда система переходит от одного устойчивого состояния к нескольким возможным состояниям, и осколок, когда система разделяется на две или более непересекающиеся части. Бифуркации также могут приводить к появлению сложных динамических структур, таких как фракталы.

Изучение бифуркаций позволяет узнать о возможных изменениях в системе и предсказать ее будущее поведение. Это может быть полезно во многих областях, включая физику, экономику, биологию и теорию управления.

Как возникает бифуркация?

Возникновение бифуркации происходит, когда система достигает критического значения параметра. При этом происходит изменение структуры решений и переход системы из одного устойчивого состояния в другое. Такое изменение может быть непредсказуемым и иметь качественный характер.

Примером бифуркации является бифуркация Хопфа. В этом случае, при изменении значения параметра, система переходит от устойчивого состояния, когда все траектории системы сходятся к равновесию, к состоянию, когда траектории системы описывают периодические колебания.

Значение бифуркации заключается в том, что она позволяет понять, как изменение параметров может влиять на поведение системы. Используя математическую модель и анализ бифуркаций, можно предсказать, как система будет вести себя в различных условиях и принять соответствующие меры для управления системой.

Классификация бифуркаций

Статические бифуркации представляют собой изменения в равновесных состояниях системы. Они возникают при изменении параметров системы и приводят к появлению или исчезновению равновесных точек или устойчивых циклов. Примерами статических бифуркаций являются бифуркация седло-узел и бифуркация бифуркаций.

Динамические бифуркации, в отличие от статических, связаны с изменениями в динамике системы. Они проявляются в изменении формы и структуры фазовых траекторий системы при изменении параметров. Примерами динамических бифуркаций являются бифуркация Неймарка-Сакера и бифуркация Хопфа.

Кроме того, бифуркации могут быть классифицированы по типу системы и типу параметра, который вызывает бифуркацию. Например, бифуркации могут быть классифицированы для дискретных или непрерывных систем, а также для изменения параметров системы или внешних воздействий.

Классификация бифуркаций играет важную роль в анализе динамических систем. Она позволяет выявить основные механизмы изменения динамики системы и предсказать ее будущее поведение.

Приложения бифуркаций в математике

Бифуркации широко применяются в математике для изучения различных систем и процессов. Они позволяют анализировать изменения в системе при изменении параметров и выявлять критические точки, при которых происходят существенные изменения в поведении системы.

Одним из основных приложений бифуркаций является исследование динамических систем. Бифуркационный анализ позволяет определить различные типы поведения системы в зависимости от параметров. Например, при анализе системы дифференциальных уравнений можно выявить различные типы устойчивости равновесных состояний системы при изменении параметров.

Бифуркации также активно используются в теории хаоса. Изучение бифуркаций позволяет понять, как система может переходить из устойчивого состояния в хаотическое состояние при изменении входных параметров. Это позволяет прогнозировать и контролировать хаотическое поведение систем, таких как популяции животных, электронные колебания и другие.

Бифуркации также находят применение в физике, биологии, экономике и других науках. Они позволяют исследовать различные физические и биологические процессы, такие как фазовые переходы, колебания в химических реакциях, изменения популяций и многие другие.

В заключение, бифуркации имеют большое значение в математике и других науках, так как они позволяют анализировать и понимать сложное поведение систем и процессов. Изучение бифуркаций помогает предсказывать и контролировать различные явления и придает математической теории глубину и практическую значимость.

Вопрос-ответ:

Что такое бифуркация в математике?

Бифуркация в математике – это качественное изменение динамики системы при изменении параметров. В простых словах, это переход системы из одного состояния в другое при изменении внешних условий.

Какие примеры бифуркации существуют в математике?

Примеры бифуркации в математике можно найти в различных областях, таких как дифференциальные уравнения, динамические системы и теория хаоса. Например, бифуркация может происходить при изменении параметров в системе лотки-вольтерра, что приводит к изменению ее устойчивости и возникновению новых устойчивых состояний.

Какое значение имеет бифуркация в математике?

Бифуркация имеет большое значение в математике, так как позволяет изучать качественные изменения в системе и понять ее поведение при изменении параметров. Это позволяет предсказывать возможные состояния и переходы системы, а также анализировать ее стабильность.

Как можно представить бифуркацию в графическом виде?

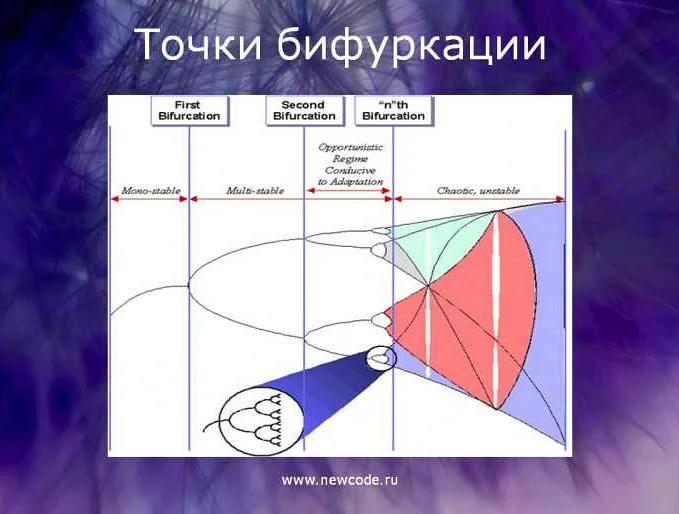
Бифуркацию можно представить в графическом виде с помощью диаграммы бифуркации. На такой диаграмме по оси абсцисс отображается значение параметра, а по оси ординат – состояние системы. На диаграмме видны точки бифуркации, где происходит изменение состояния системы.

Какие приложения имеет бифуркация в реальном мире?

Бифуркация имеет много приложений в реальном мире. Например, она применяется в биологии для изучения популяций и экосистем, в экономике для анализа экономических моделей, а также в физике и химии для изучения различных процессов. Понимание бифуркации помогает предсказывать и контролировать поведение сложных систем.

Что такое бифуркация в математике?

Бифуркация в математике — это точка или момент, когда система переходит из одного состояния в другое. Она характеризуется изменением структуры системы и возникновением новых состояний или поведения.

История изучения бифуркаций

Изучение бифуркаций началось в XIX веке, когда математики и физики стали осознавать, что некоторые системы динамических уравнений могут проявлять неожиданные изменения в своем поведении при изменении параметров. Однако понятие бифуркации как такового еще не существовало, и первые исследования были проведены на практике без строгого математического аппарата.

Первый шаг в понимании бифуркаций сделал французский математик Анри Пуанкаре в конце XIX — начале XX века. Он внес значительный вклад в область теории дифференциальных уравнений и динамических систем. Пуанкаре стал изучать поведение системы на плоскости фазовых переменных и обнаружил, что при определенных значениях параметров траектории системы могут меняться кардинальным образом.

В 1960-х годах интерес к бифуркациям снова возрос, а исследования в этой области стали более систематическими и математическими. Важный вклад в развитие теории бифуркаций внесли такие ученые, как Рене Том, Дэвид Руэл, Хаскелл Айнсворт и другие. Их работы позволили установить более общие принципы и определения для изучения бифуркаций.

Сегодня изучение бифуркаций является важной частью динамических систем и находит применение в различных областях, таких как физика, биология, химия и экономика. Благодаря изучению бифуркаций возможно предсказывать и объяснять различные явления, происходящие в сложных системах.

Видео по теме: