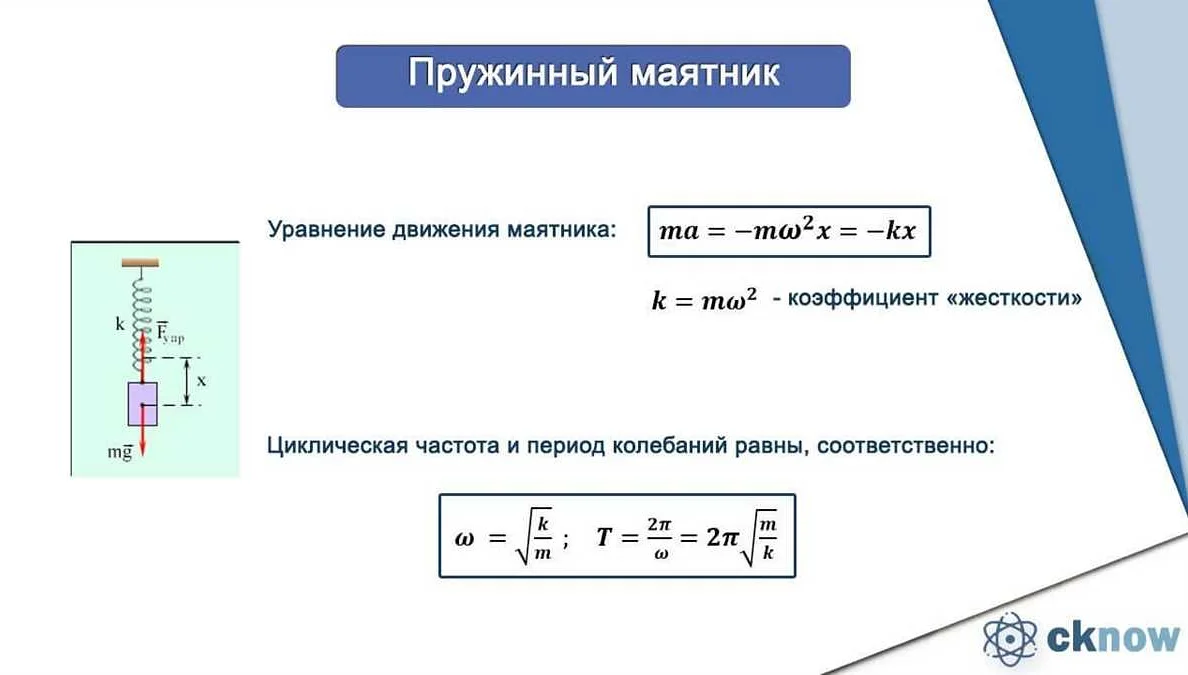
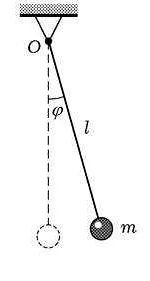
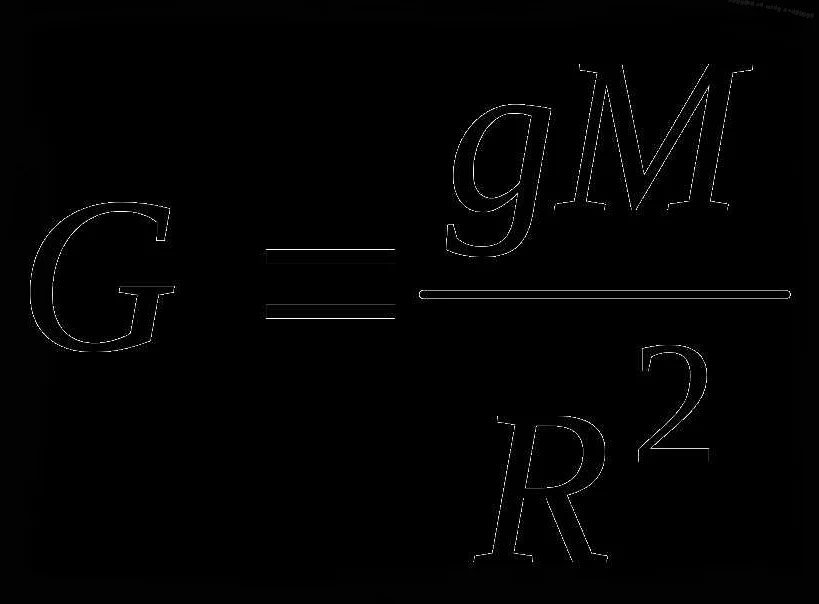Как изменится частота колебаний математического маятника, если его частота свободных малых колебаний равна 1 Гц?

Если частота свободных малых колебаний математического маятника равна 1 Гц, то в дальнейших колебаниях его частота останется такой же.

Математический маятник — это один из наиболее распространенных примеров объекта, используемого для демонстрации основ законов физики. Математический маятник — это идеализированная модель маятника, который не имеет массы, но имеет длину и представляет собой систему, которая может колебаться вокруг вертикальной оси.

Основная характеристика колебаний математического маятника — это частота колебаний. Частота колебаний — это количество колебаний, которые система может выполнить за единицу времени. Частота колебаний определяется длиной маятника и силой тяжести.

Одним из интересных вопросов, которые могут возникнуть при исследовании математического маятника, является то, что произойдет с частотой колебаний при изменении частоты свободных малых колебаний до 1 Гц. В данной статье будут рассмотрены перспективы и последствия такого изменения частоты.

Последствия изменения частоты свободных малых колебаний математического маятника до 1 Гц

Математический маятник является простейшей моделью колебательной системы, характеризующейся свободными малыми колебаниями. Частота этих колебаний зависит от длины маятника и ускорения свободного падения и может быть вычислена по формуле:

f = 1/2π √(g/l),

где g — ускорение свободного падения, l — длина маятника.

Если изменить длину маятника или ускорение свободного падения, то изменится и частота свободных малых колебаний. Например, при изменении длины маятника до такой величины, чтобы частота колебаний составляла 1 Гц, произойдут следующие изменения:

• Частота свободных малых колебаний станет равной 1 Гц;
• Период колебаний увеличится до 1 секунды;
• Амплитуда колебаний может измениться в зависимости от внешних условий и сил, действующих на маятник;
• Скорость и частота изменения энергии колебательной системы также могут быть изменены;
• Устойчивость системы может быть нарушена, если изменить другие параметры системы, такие как масса маятника или коэффициент сопротивления воздуха.

Таким образом, изменение частоты свободных малых колебаний математического маятника до 1 Гц может привести к различным изменениям в колебательной системе и состоянии маятника в целом.

Что такое свободные малые колебания математического маятника?

Математический маятник – это инерционно-гравитационная система, которая состоит из точечной массы, связанной с невесомой стержней или нитью. Под свободными малыми колебаниями понимаются колебания маятника без внешнего воздействия. Это означает, что маятник свободно колеблется в своей положительной или отрицательной стороне, пока не происходит остановка или изменение направления движения.

При свободных малых колебаниях математического маятника совершение одного полного колебания занимает определенное количество времени, называемое периодом. Величина периода колебаний зависит от длины маятника, массы точки и силы тяжести – чем меньше масса и длина, тем меньше период. Кроме того, изменение частоты свободных малых колебаний математического маятника может произойти в результате изменения этих факторов, а также изменения условий окружающей среды.

Изменение частоты свободных малых колебаний математического маятника может иметь негативные последствия, например, на точность измерений времени. Поэтому важно учитывать все факторы, влияющие на частоту колебаний, при проектировании и эксплуатации математического маятника.

Влияние изменения частоты на свободные малые колебания математического маятника

Математический маятник — это один из простейших объектов механики, характеризующийся свободным движением вокруг точки подвеса. Изменение частоты колебаний этого маятника может привести к значительным последствиям, которые следует учитывать при работе с ним.

Изменение частоты колебаний математического маятника до 1 Гц приводит к тому, что влияние сопротивления воздуха и других факторов становится заметным. Это может привести к снижению амплитуды колебаний, уменьшению периода и даже к полной остановке маятника за счет эффекта диссипации энергии.

В связи с этим следует учитывать частотные характеристики математического маятника при подборе оборудования и настройке эксперимента. Также следует иметь в виду, что изменение частоты может привести к изменению формы колебаний, что в свою очередь может повлиять на точность проводимых измерений.

Также стоит отметить, что изменение частоты колебаний может повлиять на устойчивость маятника и на возможность реализации некоторых экспериментов. Все эти факторы следует учитывать при работе с математическим маятником и при проведении соответствующих исследований.

Таким образом, изменение частоты свободных малых колебаний математического маятника может привести к значительным последствиям, которые следует учитывать при работе с ним. Это может повлиять на точность измерений, устойчивость маятника и возможность проведения экспериментов. Поэтому необходимо учитывать частотные характеристики маятника при выборе оборудования и настройке эксперимента.

Что происходит с частотой колебаний при изменении до 1 Гц?

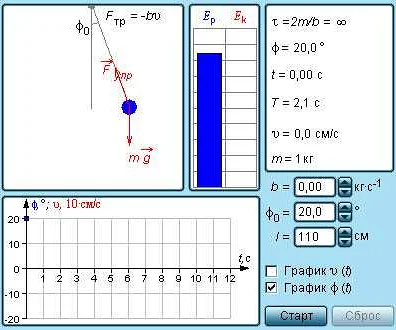
При изменении частоты свободных малых колебаний математического маятника до 1 Гц происходит заметное уменьшение частоты колебаний. Это объясняется тем, что при уменьшении частоты свободных колебаний математического маятника увеличивается его период колебаний.

Обычно частота свободных малых колебаний математического маятника составляет несколько герц, что обеспечивает быстрые колебания. Однако, если уменьшить частоту колебаний до 1 Гц, то маятник будет колебаться медленнее, что может отразиться на его поведении в системе, где он используется.

Уменьшение частоты свободных малых колебаний математического маятника может быть вызвано различными факторами, такими как изменение массы маятника, его длины или жесткости подвеса. Поэтому, для предотвращения необходимо проводить регулярную проверку системы, в которую входит математический маятник, и проводить необходимые корректировки, если это необходимо.

Как изменение частоты свободных малых колебаний влияет на амплитуду колебаний?

Частота свободных малых колебаний математического маятника определяется его массой и длиной подвеса. Изменение любого из этих параметров может привести к изменению частоты колебаний.

Однако, изменение частоты колебаний также может оказать влияние на амплитуду колебаний. Согласно закону сохранения энергии, период колебаний обратно пропорционален корню из длины подвеса маятника. При уменьшении частоты колебаний до 1 Гц, длина подвеса должна увеличиться, чтобы поддерживать тот же период колебаний. В итоге, при большей длине подвеса меньше будет затрачиваться энергии на преодоление сил сопротивления воздуха и маятник будет колебаться с большей амплитудой.

Кроме того, частота колебаний также может оказать влияние на резонансную частоту системы. Приближение частоты колебаний к резонансной частоте может привести к увеличению амплитуды свободных колебаний.

В целом, изменение частоты свободных малых колебаний влияет на амплитуду колебаний, а также на другие параметры системы колебаний, такие как перемещение, скорость и сила.

Влияние изменения частоты на положение равновесия математического маятника

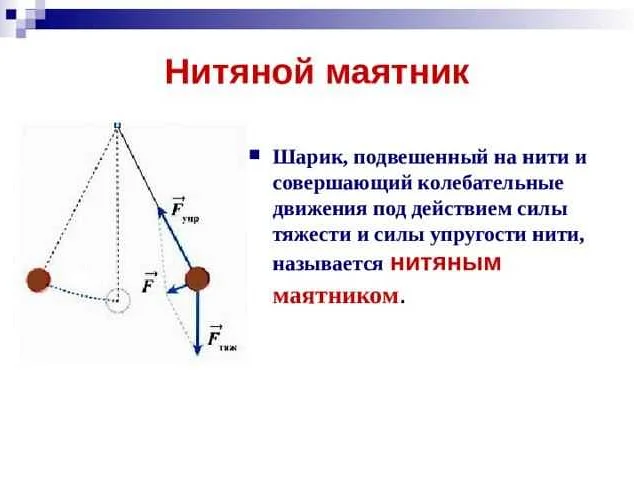
Математический маятник — это система, в которой груз подвешен на тонкой нити и способен колебаться вокруг вертикальной оси. Такая система является одной из самых простых в механике и широко используется в исследованиях. Но что произойдет, если мы изменим частоту свободных малых колебаний математического маятника до 1 Гц?

Изменение частоты свободных малых колебаний математического маятника до 1 Гц может привести к изменению положения равновесия груза. В этом случае груз может переместиться из своего исходного положения на новое, что может привести к смещению центра тяжести всей системы. Кроме того, изменение частоты может привести к уменьшению амплитуды колебаний и увеличению времени осцилляции.

Следует также отметить, что изменение частоты свободных малых колебаний математического маятника до 1 Гц может вызвать эффект резонанса. Резонанс — это явление, при котором система начинает колебаться в ритме внешнего возмущения. Если частота раздражающей силы совпадает с частотой собственных колебаний системы, то амплитуда колебаний может возрасти до очень больших значений.

В целом, изменение частоты свободных малых колебаний математического маятника до 1 Гц может привести к некоторым изменениям в работе системы, и, в зависимости от условий эксперимента, может как положительно, так и отрицательно сказаться на получаемых результатах.

Как изменение частоты свободных малых колебаний влияет на период колебаний?

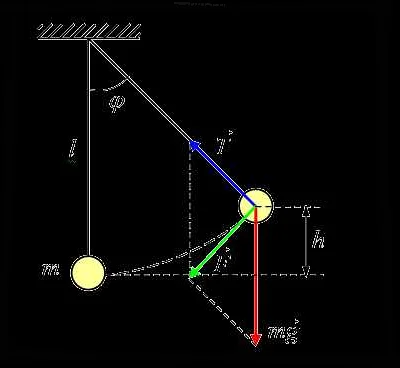
Период колебаний математического маятника зависит от частоты свободных малых колебаний. Частота колебаний обратно пропорциональна периоду, поэтому при уменьшении частоты, период увеличивается. То есть, чем реже маятник колеблется, тем больше времени требуется на одно полное колебание. Например, если частота колебаний уменьшится до 1 Гц, то период колебаний увеличится до 1 секунды.

Изменение частоты может произойти, например, за счет изменения массы маятника или длины подвеса. Если масса увеличивается, то частота уменьшается, а период увеличивается. Если длина подвеса увеличивается, то частота также уменьшается, поскольку для того, чтобы маятник совершил полный оборот, ему нужно пройти большее расстояние. Кроме того, длина подвеса может влиять на силу тяжести, что также влияет на частоту колебаний.

Изменение частоты свободных малых колебаний может оказать влияние на различные системы и процессы. Например, при проектировании маятниковых часов или амплитудных фильтров необходимо учитывать зависимость частоты от периода и наоборот, чтобы достичь нужной точности или эффективности работы этих устройств.

1. Выводы:
2. Период колебаний увеличивается при уменьшении частоты свободных малых колебаний.
3. Изменение массы или длины подвеса может повлиять на частоту колебаний и, соответственно, на период.
4. Частота колебаний и период колебаний важны для проектирования различных систем и процессов.

Как изменение частоты свободных малых колебаний влияет на переход к режиму гармонических колебаний?

Частота свободных малых колебаний математического маятника является основной характеристикой, описывающей его динамику. При изменении частоты свободных колебаний до 1 Гц происходит переход к режиму гармонических колебаний. В таком режиме маятник осциллирует с постоянной амплитудой на частоте, определяемой величиной ему свойственной массы и строением системы подвеса.

Для достижения режима гармонических колебаний, важно учитывать и задавать частоту свободных малых колебаний как настройку системы. Изменение этой частоты может привести к изменению режима колебаний, вызвать резонанс, а в некоторых случаях и к катастрофическому поведению системы.

Кроме того, при увеличении амплитуды колебаний могут происходить искажения формы колебаний, появляться дополнительные гармоники и шум. При совместном изменении амплитуды и частоты свободных малых колебаний, возможны нежелательные взаимодействия и наложения колебаний внутри системы.

В целом, изменение частоты свободных малых колебаний математического маятника до 1 Гц может привести к переходу к режиму гармонических колебаний, но требует внимательного и точного настройки системы.

Как изменение частоты свободных малых колебаний влияет на расходы энергии?

Изменение частоты свободных малых колебаний математического маятника до 1 Гц может привести к существенным изменениям в расходах энергии. Основной параметр, который определяет расходы энергии при колебаниях, это частота колебаний маятника.

При уменьшении частоты колебаний до 1 Гц, энергия, затрачиваемая на поддержание колебаний, также уменьшится. Это связано с тем, что при низкой частоте колебаний маятник тратит меньше энергии на преодоление сопротивления среды и других факторов, которые уменьшают амплитуду колебаний.

Однако, при частотах колебаний маятника ниже 1 Гц, возможно возникновение резонанса, что может привести к большим расходам энергии на поддержание колебаний.

Таким образом, изменение частоты свободных малых колебаний математического маятника влияет на расходы энергии и необходимо учитывать этот параметр при выборе параметров колебательной системы.

Видео по теме:

Вопрос-ответ:

Как изменение частоты влияет на маятник?

Частота свободных малых колебаний математического маятника – это количество колебаний, совершаемых маятником в секунду. Изменение этой частоты может привести к различным последствиям, о которых мы расскажем в дальнейшем.

Что произойдет, если частота колебаний маятника будет больше 1 Гц?

Если частота свободных малых колебаний математического маятника будет больше 1 Гц, то маятник будет колебаться быстрее, чем обычно. Это может привести к тому, что амплитуда колебаний будет меньше, а энергия маятника будет быстрее расходоваться.

Как изменение частоты связано с амплитудой колебаний?

Изменение частоты свободных малых колебаний математического маятника может повлиять на амплитуду колебаний. При изменении частоты маятника амплитуда может как увеличиться, так и уменьшиться. Это зависит от многих факторов, включая длину подвеса, массу и жесткость маятника.

Могут ли изменения частоты повлиять на период колебаний маятника?

Да, изменения частоты свободных малых колебаний математического маятника могут повлиять на его период колебаний. Период колебаний – это время, за которое маятник совершает один полный цикл колебаний. При изменении частоты маятника может измениться и его период.

Что произойдет, если частота колебаний маятника будет меньше 1 Гц?

Если частота свободных малых колебаний математического маятника будет меньше 1 Гц, то маятник будет колебаться медленнее, чем обычно. Это может привести к тому, что амплитуда колебаний будет больше, а энергия маятника будет медленнее расходоваться.

Как изменение частоты связано с эффектом резонанса?

Изменение частоты свободных малых колебаний математического маятника может привести к эффекту резонанса. Резонанс возникает, когда частота внешнего воздействия совпадает с собственной частотой колебаний системы. В этом случае возможно возрастание амплитуды колебаний, что может привести к разрушению системы.

Может ли изменение частоты свободных малых колебаний математического маятника повлиять на его устойчивость?

Да, изменение частоты свободных малых колебаний математического маятника может повлиять на его устойчивость. Устойчивость – это способность системы возвращаться в исходное положение после малых отклонений. При изменении частоты маятника его устойчивость может как увеличиться, так и уменьшиться, в зависимости от многих факторов.

Влияние изменения частоты на декремент затухания колебаний математического маятника

Декремент затухания колебаний является одним из основных параметров колебательной системы. Он определяет скорость ослабления амплитуды колебаний со временем. Существует прямая зависимость между декрементом затухания и частотой свободных колебаний математического маятника.

При изменении частоты свободных колебаний, декремент затухания также изменяется. При уменьшении частоты свободных колебаний до 1 Гц, декремент затухания уменьшается. Это происходит из-за того, что при меньшей частоте колебаний, маятник не успевает раскачиваться настолько, чтобы скомпенсировать силы сопротивления воздуха, и поэтому амплитуда колебаний сохраняется на более длительное время.

Однако, с увеличением частоты колебаний декремент затухания повышается. Это происходит из-за более быстрой скорости раскачивания маятника, что приводит к более интенсивному воздействию сил сопротивления, и соответственно, к более быстрому затуханию колебаний.

Таким образом, изменение частоты свободных колебаний математического маятника может повлиять на декремент затухания колебаний. Это следует учитывать при проектировании и создании колебательных систем, особенно с точки зрения стабильности и длительности колебаний.

Практическое применение изменения частоты свободных малых колебаний математического маятника

Одним из практических применений изменения частоты свободных малых колебаний математического маятника является использование его в науке и технике для измерения различных физических величин. Например, частота колебаний маятника может быть использована для измерения гравитационного поля Земли или для определения ускорения свободного падения.

Также, изменение частоты колебаний может быть полезным в изучении электронных цепей, особенно в контексте резонанса. В данном случае, изменение частоты внешнего возбуждающего поля может привести к увеличению амплитуды колебаний в цепи и возможности передачи большего энергетического потенциала.

В качестве прибора измерения, математический маятник может быть использован в лаборатории для изучения механики и физики. Например, изменение частоты колебаний маятника может помочь в определении его массы или длины.

Наконец, изменение частоты свободных малых колебаний математического маятника может иметь практическое применение в строительстве и архитектуре. Например, частота колебаний маятника может быть использована для определения динамической устойчивости зданий и сооружений, что может помочь предотвратить возможные катастрофы.