Что такое дискриминант в математике

Дискриминант в математике — это показатель, который помогает определить количество и тип решений квадратного уравнения. Узнайте, как вычислить дискриминант и как он связан с графиком квадратного уравнения.

Дискриминант – это одна из ключевых характеристик квадратного уравнения. Он позволяет определить, сколько корней имеет данное уравнение и какие они. В математике, дискриминант является важным инструментом для анализа квадратных уравнений и решения множества задач.

Определение дискриминанта можно представить следующим образом: дискриминант квадратного уравнения ax^2 + bx + c = 0 с коэффициентами a, b и c равен величине D = b^2 — 4ac.

Знание дискриминанта позволяет быстро и эффективно определить, имеет ли уравнение вещественные корни, один или два комплексных корня.

Дискриминант может принимать различные значения в зависимости от коэффициентов уравнения. Если D > 0, то уравнение имеет два различных вещественных корня. Если D = 0, то уравнение имеет один вещественный корень. Если D < 0, то уравнение имеет два комплексных корня.

Рассмотрим пример, чтобы лучше понять, как работает дискриминант. Рассмотрим квадратное уравнение x^2 — 6x + 5 = 0. Сначала вычислим дискриминант по формуле: D = (-6)^2 — 4 * 1 * 5 = 36 — 20 = 16. Так как D > 0, уравнение имеет два различных вещественных корня.

Что такое дискриминант в математике?

Дискриминант обозначается символом D и вычисляется по формуле D = b^2 — 4ac. Он позволяет определить, сколько корней у квадратного уравнения и какие именно корни оно имеет.

В зависимости от значения дискриминанта D, квадратное уравнение может иметь три случая:

1. Если D > 0, то у уравнения два различных вещественных корня.
2. Если D = 0, то у уравнения есть один вещественный корень, который является двукратным.
3. Если D < 0, то у уравнения нет вещественных корней, а имеет два комплексных корня.

Дискриминант позволяет анализировать квадратные уравнения и предоставляет информацию о количестве и типе корней, которые они имеют. В математике он играет важную роль при решении квадратных уравнений и в различных областях, где требуется работа с квадратными функциями.

Видео по теме:

Определение дискриминанта в математике

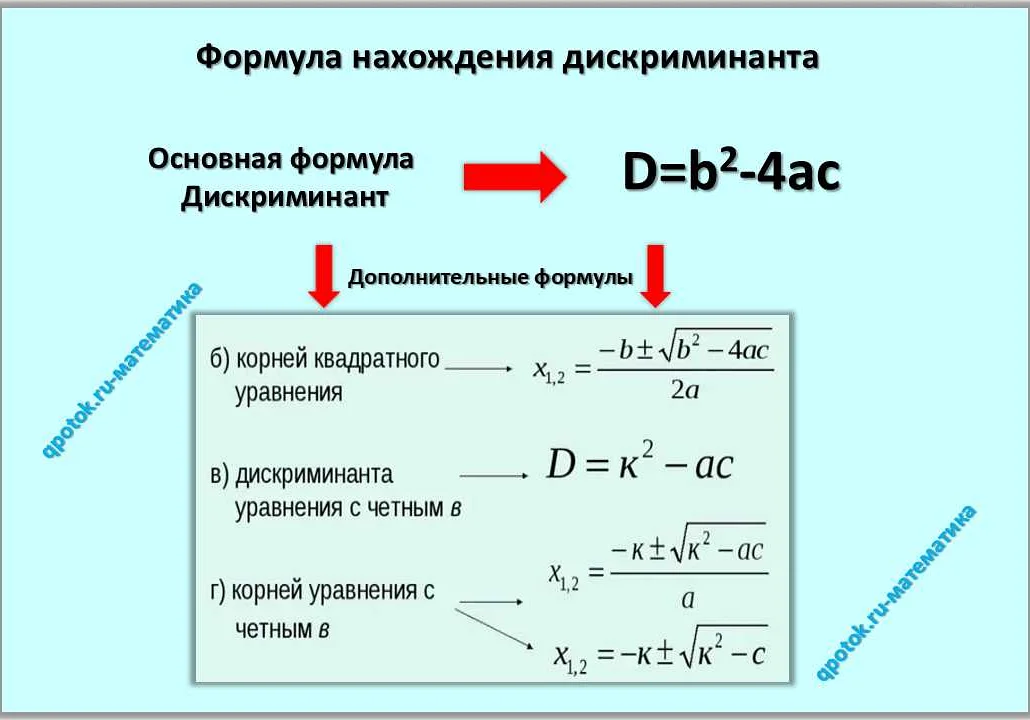
Дискриминант:

D = b^2 — 4ac

Где a, b и c — это коэффициенты квадратного уравнения.

Значение дискриминанта позволяет определить, какие корни имеет квадратное уравнение:

• Если дискриминант положителен (D > 0), то квадратное уравнение имеет два различных вещественных корня.
• Если дискриминант равен нулю (D = 0), то квадратное уравнение имеет один вещественный корень.
• Если дискриминант отрицателен (D < 0), то квадратное уравнение не имеет вещественных корней, а имеет два комплексно-сопряженных корня.

Значение дискриминанта важно при решении квадратных уравнений и позволяет более полно понять их свойства.

Формула дискриминанта в квадратном уравнении

Для квадратного уравнения вида ax^2 + bx + c = 0, дискриминант вычисляется с помощью формулы:

D = b^2 — 4ac

Где:

• a — коэффициент при x^2
• b — коэффициент при x
• c — свободный член
• D — дискриминант

Дискриминант позволяет определить количество и тип корней квадратного уравнения. Если D больше нуля, то уравнение имеет два различных вещественных корня. Если D равен нулю, то уравнение имеет один вещественный корень. Если D меньше нуля, то уравнение не имеет вещественных корней.

Как определить количество корней уравнения по значению дискриминанта?

1. 1. Если дискриминант больше нуля (D > 0), то уравнение имеет два различных корня. Например, если квадратное уравнение имеет вид ax^2 + bx + c = 0, то корни можно найти по формуле:

x1 = (-b + sqrt(D)) / (2a)

x2 = (-b — sqrt(D)) / (2a)

1. 1. Если дискриминант равен нулю (D = 0), то уравнение имеет один корень, который является вещественным и совпадает с вершиной параболы. Формула для нахождения этого корня выглядит следующим образом:

x = -b / (2a)

1. 1. Если дискриминант меньше нуля (D < 0), то уравнение не имеет вещественных корней. В этом случае решение квадратного уравнения будет комплексным и представляет собой пару комплексно-сопряженных чисел. Вычисление таких корней требует использования мнимой единицы i. Формула для нахождения корней имеет вид:

x1 = (-b + sqrt(|D|) * i) / (2a)

x2 = (-b — sqrt(|D|) * i) / (2a)

Зная значение дискриминанта, можно точно определить количество корней квадратного уравнения и найти их значения используя соответствующие формулы.

Примеры вычисления дискриминанта

Рассмотрим несколько примеров вычисления дискриминанта для квадратных уравнений:

1. Уравнение: 2x^2 + 5x — 3 = 0

   Коэффициенты: a = 2, b = 5, c = -3

   Дискриминант: D = b^2 — 4ac = 5^2 — 4*2*(-3) = 25 + 24 = 49

2. Уравнение: x^2 — 6x + 9 = 0

   Коэффициенты: a = 1, b = -6, c = 9

   Дискриминант: D = b^2 — 4ac = (-6)^2 — 4*1*9 = 36 — 36 = 0

3. Уравнение: 3x^2 + 2x + 1 = 0

   Коэффициенты: a = 3, b = 2, c = 1

   Дискриминант: D = b^2 — 4ac = 2^2 — 4*3*1 = 4 — 12 = -8

В первом примере дискриминант равен 49, что означает, что у уравнения два различных корня. Во втором примере дискриминант равен 0, что означает, что у уравнения один корень кратности 2. В третьем примере дискриминант равен -8, что означает, что у уравнения нет действительных корней.

Дискриминант и его связь с графиком квадратного уравнения

Дискриминант квадратного уравнения определяется по формуле:

Д = b2 — 4ac

где a, b и c — коэффициенты квадратного уравнения вида ax2 + bx + c = 0.

Значение дискриминанта позволяет сделать следующие выводы:

• Если дискриминант D > 0, то у уравнения два различных вещественных корня. График квадратного уравнения пересекает ось абсцисс в двух точках.
• Если дискриминант D = 0, то у уравнения есть один вещественный корень. График квадратного уравнения касается оси абсцисс в одной точке.
• Если дискриминант D < 0, то у уравнения нет вещественных корней. График квадратного уравнения не пересекает ось абсцисс.

Связь между дискриминантом и графиком квадратного уравнения позволяет наглядно представить, как влияют коэффициенты уравнения на его геометрическую интерпретацию. Это позволяет легко определить, сколько и какие корни имеет уравнение, а также примерно представить их расположение на графике.

Дискриминант и его роль в решении задач

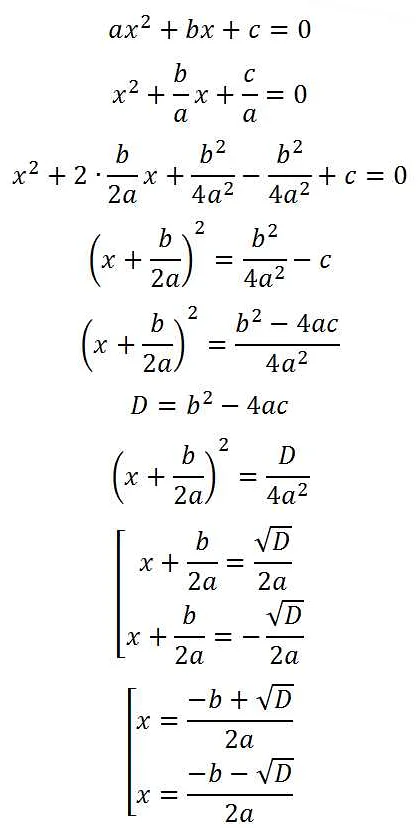
Роль дискриминанта в решении задач состоит в том, что он помогает нам определить, какие значения переменных являются корнями уравнения, а какие – нет. Зная значение дискриминанта, мы можем сделать выводы о том, какова природа корней и как они связаны с исходной задачей.

Например, если дискриминант положителен, то у уравнения есть два различных вещественных корня. Это может означать, что в задаче есть два различных решения или два возможных исхода события.

Если дискриминант равен нулю, то у уравнения есть один вещественный корень. Это может означать, что задача имеет только одно решение или только один возможный исход.

Если дискриминант отрицателен, то у уравнения нет вещественных корней. В этом случае задача может не иметь решения или не иметь возможного исхода, который удовлетворяет условию задачи.

Таким образом, дискриминант играет важную роль в решении задач, позволяя нам понять характер и количество решений уравнения. Это помогает нам принять решение или сделать выводы на основе полученных математических данных.

Интересные факты о дискриминанте

• Знак дискриминанта может быть использован для определения типа корней уравнения. Если дискриминант положителен, то уравнение имеет два различных действительных корня. Если дискриминант равен нулю, то уравнение имеет один действительный корень кратности два. Если дискриминант отрицателен, то уравнение имеет два комплексных корня.
• Значение дискриминанта может быть использовано для определения вида графика квадратного уравнения. Если дискриминант положителен, то график уравнения представляет собой параболу, открытую вверх или вниз. Если дискриминант равен нулю, то график уравнения представляет собой параболу, касающуюся оси абсцисс. Если дискриминант отрицателен, то график уравнения представляет собой параболу, не пересекающую ось абсцисс.
• Дискриминант также может быть использован для определения области значений квадратного уравнения. Если дискриминант положителен, то область значений уравнения – это весь набор действительных чисел. Если дискриминант равен нулю, то область значений уравнения состоит только из одного числа, равного корню уравнения. Если дискриминант отрицателен, то область значений уравнения не существует, так как уравнение не имеет действительных корней.

Это лишь некоторые интересные факты о дискриминанте. Он имеет еще много других свойств и применений в математике, которые могут быть изучены более подробно.

Вопрос-ответ:

Что такое дискриминант в математике?

Дискриминант — это значение, которое вычисляется по формуле и используется для определения характеристик квадратного уравнения. Он показывает, сколько корней имеет уравнение и какие они.

Как вычислить дискриминант?

Дискриминант квадратного уравнения вычисляется по формуле D = b^2 — 4ac, где a, b и c — это коэффициенты уравнения. Значение дискриминанта позволяет определить, сколько корней имеет уравнение и какие они.

Какие значения дискриминанта могут быть при решении квадратного уравнения?

Значение дискриминанта может быть положительным, отрицательным или равным нулю. Если дискриминант больше нуля, то уравнение имеет два различных вещественных корня. Если дискриминант равен нулю, то уравнение имеет один вещественный корень. Если дискриминант меньше нуля, то уравнение имеет два комплексных корня.

Можете привести примеры использования дискриминанта в математике?

Конечно! Дискриминант используется для определения характеристик квадратного уравнения. Например, при решении уравнения x^2 — 4x + 4 = 0 мы вычисляем дискриминант D, который равен 0. Это означает, что у уравнения есть один вещественный корень x = 2. Также, при решении уравнения x^2 + 2x + 5 = 0 мы вычисляем дискриминант D, который равен -16. Это означает, что у уравнения есть два комплексных корня.