Что такое к в математике

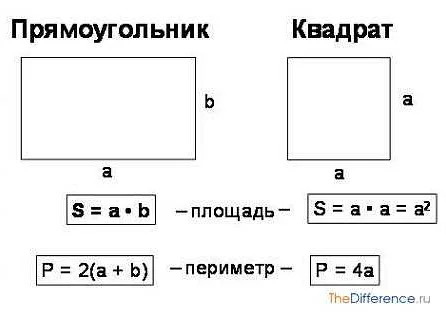
Квадрат — это геометрическая фигура, имеющая четыре равные стороны и четыре прямых угла. В математике квадрат является особой формой прямоугольника, которая имеет равные стороны и прямые углы. Узнайте, как определить площадь и периметр квадрата, а также использование квадрата в различных математических задачах.

В математике квадратное уравнение – это уравнение вида ax^2 + bx + c = 0, где a, b и c – это коэффициенты, которые могут быть любыми рациональными числами. Решение квадратного уравнения позволяет найти значения переменной x, при которых уравнение выполняется.

Квадратный корень – это операция, обратная возведению в квадрат. Он позволяет найти такое число, которое при возведении в квадрат даст исходное число. Например, квадратный корень из числа 9 равен 3, так как 3^2 = 9.

Для решения квадратного уравнения существует формула, называемая формулой дискриминанта. Дискриминант – это число, которое определяет количество и тип корней уравнения. Если дискриминант положителен, то у уравнения два различных вещественных корня. Если дискриминант равен нулю, то у уравнения есть один вещественный корень. Если дискриминант отрицателен, то у уравнения два комплексных корня.

Решение квадратного уравнения можно найти с помощью формулы: x = (-b ± √D) / (2a), где D – дискриминант уравнения.

Используя эту формулу, можно решить квадратное уравнение и найти значения переменной x. Важно помнить, что решение квадратного уравнения может быть как вещественным, так и комплексным.

Квадратное уравнение: понятие и примеры

Квадратное уравнение имеет два корня, которые могут быть вещественными или комплексными числами. Для нахождения корней квадратного уравнения можно использовать формулу дискриминанта.

Дискриминант D квадратного уравнения вычисляется по формуле D = b^2 — 4ac. В зависимости от значения дискриминанта, можно сделать выводы о количестве и типе корней:

Значение дискриминантаКоличество корнейТип корней

D > 0	2	Вещественные
D = 0	1	Вещественный, кратный
D < 0	2	Комплексные

Примеры квадратных уравнений:

1. x^2 — 5x + 6 = 0

2. 2x^2 + 3x — 2 = 0

3. 4x^2 + 4x + 1 = 0

Видео по теме:

Как определить квадратный корень?

Определение квадратного корня может быть выполнено при помощи различных методов. Одним из наиболее распространенных методов является метод приближенного извлечения квадратного корня. Он основан на последовательном приближении квадратного корня путем вычисления среднего арифметического между начальным приближением и результатом деления числа на это начальное приближение.

Также существует альтернативный метод определения квадратного корня, который основан на использовании таблиц. Этот метод позволяет найти квадратный корень числа путем последовательного сравнения квадратов чисел из таблицы с исходным числом. Когда найдется число, квадрат которого ближе всего к исходному числу, его квадратный корень будет искомым.

ЧислоКвадрат

1	1
2	4
3	9
4	16
5	25
6	36

Таким образом, определение квадратного корня является важной задачей в математике, и существует несколько методов для его нахождения. При решении квадратных уравнений, знание и понимание квадратных корней помогает найти их значения и решить уравнение.

Определение квадратного корня

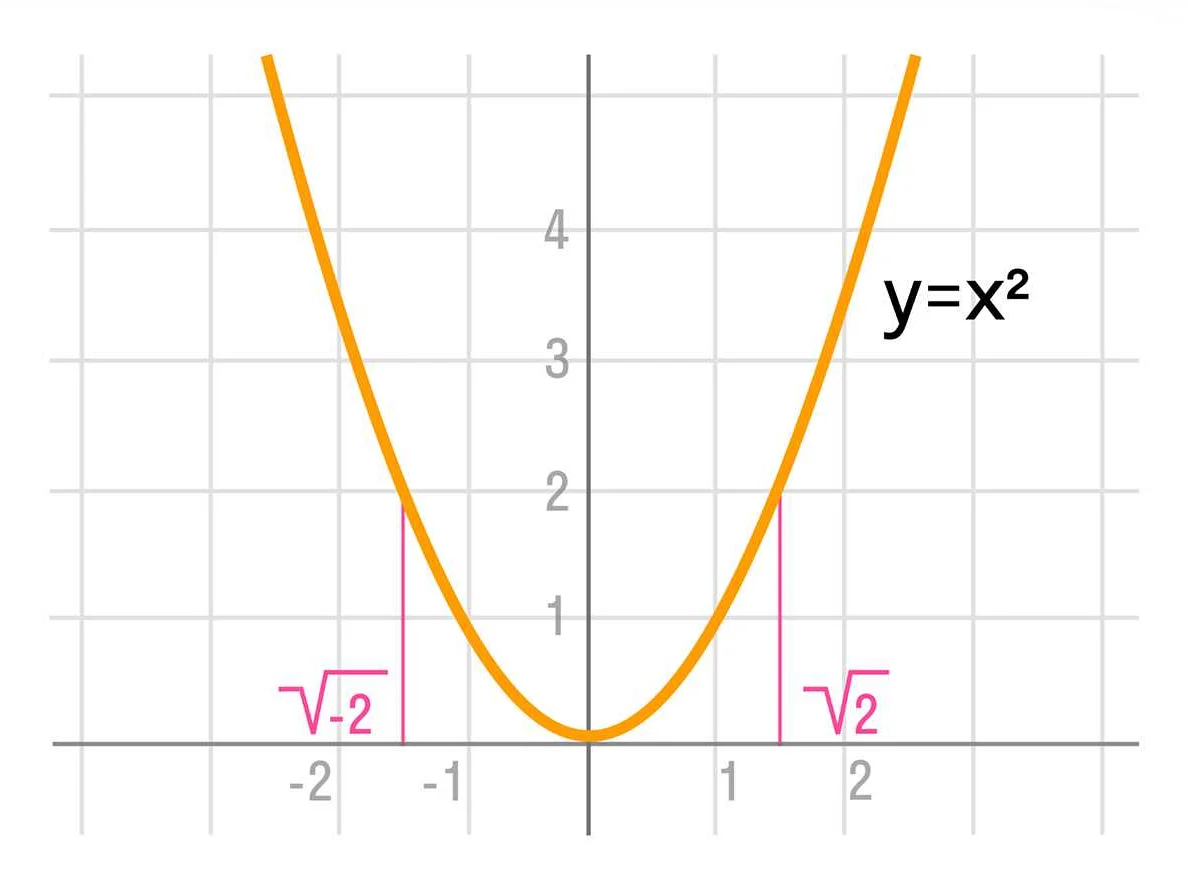
Когда мы говорим о квадратных корнях, часто имеется в виду положительный квадратный корень. Например, корень из 9 равен 3, потому что 3^2 = 9. Однако, каждое число имеет два квадратных корня: положительный и отрицательный. Например, корень из 16 равен 4 и -4, потому что и 4^2 = 16, и (-4)^2 = 16.

Квадратный корень можно представить в виде десятичной дроби. Например, корень из 2 приближенно равен 1.41421356 и так далее. Такой десятичный корень называется приближенным или десятичным корнем.

Квадратные корни широко используются в математике, физике, инженерии и других научных областях для решения различных задач. Нахождение квадратного корня является важной операцией и может быть выполнено с помощью различных методов, включая геометрический метод, метод подстановки и использование квадратного корня в качестве функции научного калькулятора или программы.

Вопрос-ответ:

Какие значения может принимать квадратный корень в математике?

Квадратный корень в математике может принимать только неотрицательные значения, так как он является результатом извлечения корня из неотрицательного числа.

Как решить квадратное уравнение с помощью квадратного корня?

Чтобы решить квадратное уравнение с помощью квадратного корня, нужно сначала выразить переменную в уравнении в виде квадрата, затем извлечь квадратный корень из обеих частей уравнения и найти значения переменной.

Можно ли найти квадратный корень отрицательного числа?

В обычной системе действительных чисел нельзя найти квадратный корень отрицательного числа, так как извлечение корня из отрицательного числа приводит к появлению комплексных чисел.

Как найти корень квадратный корень из числа?

Чтобы найти квадратный корень из числа, необходимо найти положительное число, у которого квадрат равен данному числу.

Как проверить, является ли число решением квадратного уравнения?

Чтобы проверить, является ли число решением квадратного уравнения, нужно подставить это число вместо переменной в уравнение и проверить, равенство ли получается.

Примеры нахождения квадратного корня

Пример 1:

Дано уравнение: x2 = 25. Чтобы найти значение переменной x, нужно извлечь квадратный корень из обеих частей уравнения:

x = √25.

Квадратный корень из 25 равен 5, поэтому решением уравнения будет x = 5.

Пример 2:

Дано уравнение: x2 + 5x + 6 = 0. Для нахождения корней уравнения, нужно воспользоваться формулой дискриминанта и квадратным корнем. По формуле дискриминанта D = b2 — 4ac, где a, b и c — коэффициенты уравнения. Если дискриминант D больше нуля, то уравнение имеет два различных корня.

В данном случае a = 1, b = 5 и c = 6. Подставляем значения в формулу дискриминанта:

D = 52 — 4 * 1 * 6 = 25 — 24 = 1.

Так как дискриминант больше нуля, уравнение имеет два корня. Далее, извлекаем квадратный корень из дискриминанта:

√D = √1 = 1.

Теперь, используя формулу корней уравнения, можно найти значения переменной x:

x1 = (-b + √D) / 2a = (-5 + 1) / 2 = -4 / 2 = -2

x2 = (-b — √D) / 2a = (-5 — 1) / 2 = -6 / 2 = -3

Решениями данного уравнения будут x1 = -2 и x2 = -3.

Таким образом, решение квадратного уравнения требует нахождения квадратного корня из числа, что позволяет определить значения переменной и найти решение уравнения.

Как решить квадратное уравнение?

Для решения квадратного уравнения существует несколько методов:

1. Метод Формулы Корней: используется формула дискриминанта D = b^2 — 4ac для нахождения двух корней x1 и x2. Если D больше нуля, то уравнение имеет два различных корня, если D равно нулю, то уравнение имеет один корень, и если D меньше нуля, то уравнение не имеет рациональных корней.
2. Метод Завершения Квадрата: используется для преобразования квадратного уравнения в квадрат с полным квадратом и последующим нахождением корней.
3. Графический метод: используется построение графика функции, заданной уравнением, и нахождение точек пересечения с осью x.
4. Метод Факторизации: используется разложение квадратного уравнения на множители и нахождение значений x.

Выбор метода решения квадратного уравнения зависит от его сложности и предпочтений решающего. Важно помнить, что каждый метод требует точности и внимательности при выполнении вычислений.

Метод дискриминанта

D = b² — 4ac

Затем, исходя из значения дискриминанта, можно определить количество корней и их характеристики:

• Если D > 0, то уравнение имеет два различных вещественных корня.
• Если D = 0, то уравнение имеет один вещественный корень.
• Если D < 0, то уравнение не имеет вещественных корней, но имеет два комплексных корня.

Для нахождения корней уравнения с помощью метода дискриминанта используются следующие формулы:

1. Если уравнение имеет два различных вещественных корня, то:
   • x₁ = (-b + √D) / (2a)
   • x₂ = (-b — √D) / (2a)
2. Если уравнение имеет один вещественный корень, то:
   • x = -b / (2a)
3. Если уравнение не имеет вещественных корней, то:
   • x₁ = (-b + i√|-D|) / (2a)
   • x₂ = (-b — i√|-D|) / (2a)

Метод дискриминанта позволяет найти все возможные корни квадратного уравнения. Он является удобным и эффективным инструментом для решения данного типа задач.

Примеры решения квадратного уравнения

Решение квадратного уравнения предполагает нахождение корней этого уравнения, то есть значений переменной, при которых уравнение выполняется.

Рассмотрим несколько примеров решения квадратного уравнения:

Пример 1:

Уравнение: x2 — 4x + 4 = 0

Данное уравнение является квадратным, так как степень переменной x равна 2.

Решение:

Для нахождения корней квадратного уравнения, необходимо использовать формулу дискриминанта: D = b2 — 4ac

В данном случае, уравнение имеет вид ax2 + bx + c = 0, где a = 1, b = -4 и c = 4.

Вычисляем дискриминант:

D = (-4)2 — 4 * 1 * 4 = 16 — 16 = 0

Так как дискриминант равен нулю, у уравнения есть только один корень.

Находим корень уравнения:

x = -b / 2a = -(-4) / (2 * 1) = 4 / 2 = 2

Таким образом, уравнение x2 — 4x + 4 = 0 имеет один корень x = 2.

Пример 2:

Уравнение: 3×2 + 5x — 2 = 0

Решение:

Вычисляем дискриминант:

D = 52 — 4 * 3 * (-2) = 25 + 24 = 49

Так как дискриминант равен положительному числу, у уравнения есть два различных корня.

Находим корни уравнения:

x1 = (-5 + √49) / (2 * 3) = (-5 + 7) / 6 = 2 / 6 = 1/3

x2 = (-5 — √49) / (2 * 3) = (-5 — 7) / 6 = -12 / 6 = -2

Таким образом, уравнение 3×2 + 5x — 2 = 0 имеет два корня: x1 = 1/3 и x2 = -2.

В каждом примере, найдены корни квадратного уравнения с помощью дискриминанта и формулы для нахождения корней.

Что такое вещественные и комплексные корни?

Вещественный корень — это такое значение x, при котором квадратное уравнение имеет решение в виде действительного числа. Вещественные корни могут быть положительными, отрицательными или равными нулю.

Комплексный корень — это такое значение x, при котором квадратное уравнение имеет решение в виде комплексного числа. Комплексные числа представляются в виде a + bi, где a и b — действительные числа, а i — мнимая единица (i^2 = -1).

Для определения того, какие корни имеет квадратное уравнение, можно использовать дискриминант. Дискриминант D рассчитывается по формуле D = b^2 — 4ac. Значение дискриминанта определяет тип корней:

• Если D > 0, то уравнение имеет два различных вещественных корня.
• Если D = 0, то уравнение имеет один вещественный корень (два совпадающих корня).
• Если D < 0, то уравнение имеет два комплексных корня.

Вещественные и комплексные корни являются важными концепциями в квадратном уравнении, которые позволяют определить множество его решений. Понимание этих понятий помогает рационально подходить к решению квадратных уравнений и анализу их свойств.

Как работать с квадратными корнями в математике?

Для работы с квадратными корнями в математике, сначала необходимо понять некоторые основные понятия. Квадратный корень обозначается символом √, который ставится перед выражением. Например, корень из числа 9 записывается как √9 и равен 3.

Чтобы решить квадратное уравнение с использованием квадратного корня, нужно следовать нескольким шагам:

1. Найти дискриминант уравнения. Дискриминант вычисляется по формуле D = b^2 — 4ac, где a, b и c — это коэффициенты уравнения.
2. Если дискриминант положительный (D > 0), то у уравнения есть два различных корня. Они вычисляются по формулам x = (-b + √D) / 2a и x = (-b — √D) / 2a.
3. Если дискриминант равен нулю (D = 0), то у уравнения есть один корень, который вычисляется по формуле x = -b / 2a.
4. Если дискриминант отрицательный (D < 0), то у уравнения нет решений в области действительных чисел. Такие уравнения называются комплексными, и их решение требует использования комплексных чисел.

Квадратный корень может быть использован не только для решения квадратных уравнений, но и для выполнения других математических операций, таких как упрощение выражений и нахождение длины стороны квадрата, если известна его площадь.

Важно понимать, что квадратный корень всегда имеет два значения — положительное и отрицательное. При решении квадратных уравнений необходимо учитывать оба значения и проверять их на соответствие условиям задачи.

ПримерРешение

Найти корень из 16	√16 = 4
Решить уравнение x^2 — 9 = 0	D = (-9)^2 — 4*1*(-9) = 81, x1 = (9 + √81) / 2 = 6, x2 = (9 — √81) / 2 = -3

Таким образом, работа с квадратными корнями в математике требует понимания основных понятий и умения применять соответствующие формулы для решения уравнений. Эти навыки могут быть полезны при решении различных задач из области алгебры и геометрии.

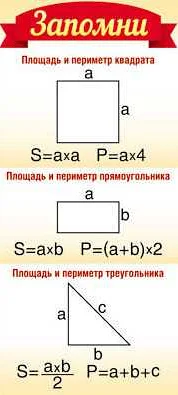
Значение квадратных корней в геометрии

В геометрии квадратный корень применяется для определения длины стороны квадрата. Если известна площадь квадрата, то квадратный корень из этой площади даст нам длину стороны квадрата.

Кроме того, квадратный корень используется для определения расстояния между двумя точками на плоскости. Если координаты этих точек заданы, то формула для вычисления расстояния между ними будет включать квадратный корень из суммы квадратов разности координат по осям x и y.

Также квадратный корень применяется в формулах для нахождения длины диагонали прямоугольника или треугольника. Например, для прямоугольника с известными сторонами a и b, длина диагонали будет равна квадратному корню из суммы квадратов длин сторон.

В геометрии квадратный корень позволяет нам вычислять длины и расстояния, используя известные значения и формулы, что помогает нам получить более точные результаты и лучше понять геометрические свойства фигур.