Что такое длина ломаной в математике

Длина ломаной в математике — это мера ее протяженности, измеряемая суммой длин всех отрезков, составляющих ломаную.

Длина ломаной – один из важных параметров, используемых в математике для описания геометрических фигур. Ломаная представляет собой набор отрезков, соединяющих точки на плоскости или в пространстве. Длина ломаной определяется как сумма длин всех отрезков, из которых она состоит. Это понятие широко применяется в геометрии, анализе и других разделах математики.

Для вычисления длины ломаной необходимо знать координаты ее вершин. Если ломаная задана на координатной плоскости, то длина каждого отрезка может быть найдена с помощью формулы расстояния между двумя точками. Далее все длины складываются, чтобы получить общую длину ломаной. Если ломаная задана в пространстве, то расстояние между двумя точками находится аналогичным образом, только с использованием трехмерных координат.

Пример использования длины ломаной: рассмотрим случай, когда необходимо найти длину периметра многоугольника. Многоугольник можно представить в виде ломаной, соединяющей вершины. Таким образом, чтобы найти периметр, необходимо найти длину этой ломаной.

Знание понятия длины ломаной позволяет решать различные задачи, связанные с геометрией и анализом. Это понятие является основой для изучения других геометрических фигур, таких как многоугольники, фракталы и т.д. Поэтому понимание длины ломаной является важным для успешного изучения математики.

Что такое длина ломаной в математике

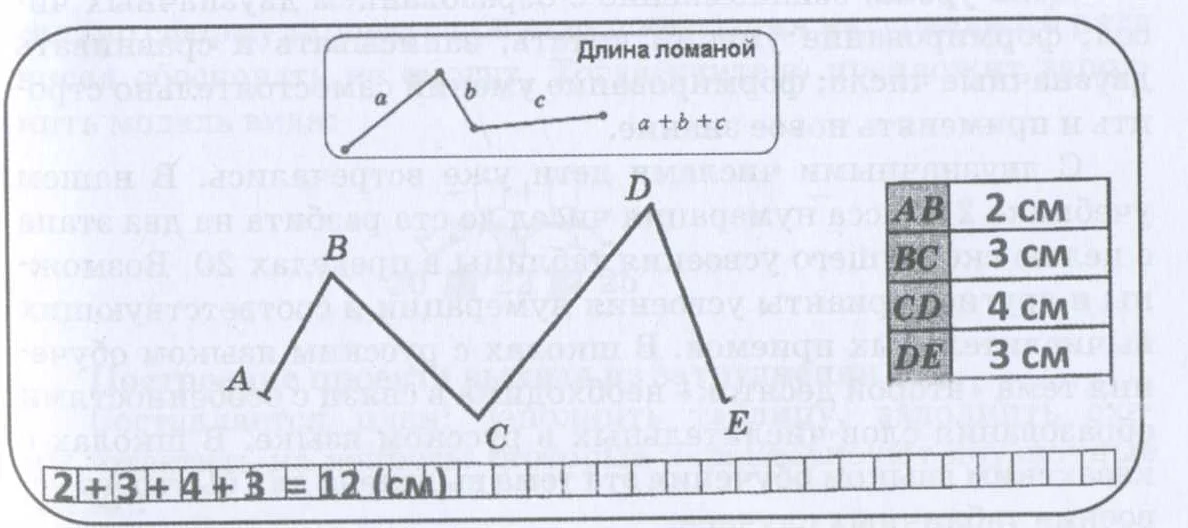
Один из простейших методов вычисления длины ломаной — это разбиение ломаной на отрезки и использование формулы для нахождения длины отрезка по координатам его концов. Если известны координаты всех точек ломаной, можно вычислить длину каждого отрезка и сложить их. Таким образом получим длину всей ломаной.

Длина ломаной может быть полезной в различных ситуациях, например, при решении задач на геометрические построения или при аппроксимации кривых. Определение длины ломаной в математике позволяет более точно изучать и описывать геометрические объекты и их свойства.

Определение длины ломаной

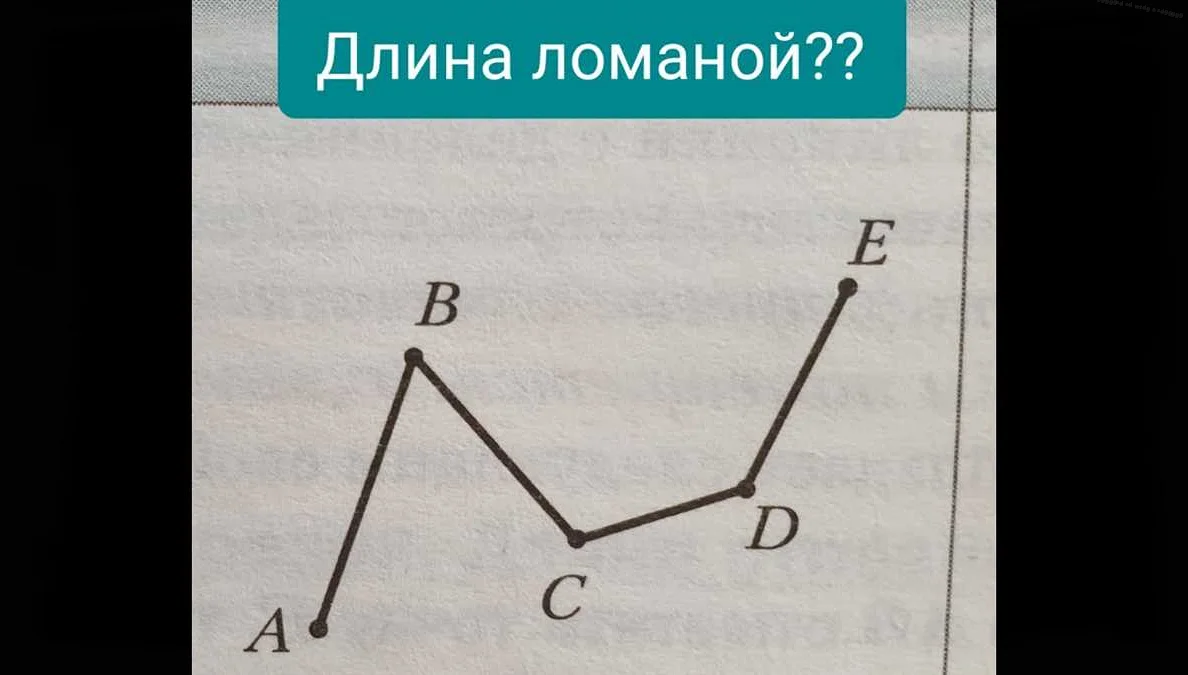
Для простых ломаных, состоящих из отрезков, длина может быть вычислена путем сложения длин каждого отдельного отрезка. Если ломаная состоит из дуг или кривых, ее длина может быть вычислена с использованием интеграла или других математических методов.

Длина ломаной играет важную роль в геометрии и анализе данных. Она может быть использована для измерения расстояний между точками, описания формы объектов и аппроксимации кривых. Вычисление длины ломаной может быть полезным инструментом в различных областях, включая физику, инженерию, компьютерную графику и статистику.

Формула для расчета длины ломаной

Пусть у нас есть ломаная, состоящая из n отрезков. Длина каждого отрезка обозначается символом Li, где i принимает значения от 1 до n. Тогда длина всей ломаной обозначается символом S и вычисляется по формуле:

S = L1 + L2 + … + Ln

Таким образом, для расчета длины ломаной необходимо знать длины всех ее отрезков и просуммировать их.

Примеры расчета длины ломаной

Длина ломаной может быть вычислена с помощью формулы длины дуги:

Длина ломаной = ∑∑ √[(xi — xi-1)2 + (yi — yi-1)2]

Рассмотрим пример вычисления длины ломаной на плоскости. Пусть дана ломаная, состоящая из трех точек:

Точка A (1, 2)

Точка B (4, 6)

Точка C (7, 4)

Для вычисления длины ломаной, нам нужно вычислить расстояние между каждой парой соседних точек и сложить эти расстояния. Расстояние между двумя точками на плоскости может быть найдено с использованием теоремы Пифагора:

Расстояние = √[(x2 — x1)2 + (y2 — y1)2]

Применяя эту формулу для каждой пары точек, получим:

Расстояние между точкой A и точкой B:

√[(4 — 1)2 + (6 — 2)2] = √[9 + 16] = √25 = 5

Расстояние между точкой B и точкой C:

√[(7 — 4)2 + (4 — 6)2] = √[9 + 4] = √13

Теперь мы можем вычислить длину ломаной, сложив все найденные расстояния:

Длина ломаной = 5 + √13

Таким образом, длина данной ломаной равна 5 + √13.

Как определить длину ломаной на координатной плоскости

Для определения длины ломаной на координатной плоскости необходимо разбить ломаную на отрезки и вычислить сумму длин этих отрезков.

Для простоты рассмотрим пример, где координаты вершин ломаной заданы числами. Пусть у нас есть ломаная, состоящая из трех вершин: A(1, 2), B(3, 4) и C(5, 6).

ВершинаКоординаты

A	(1, 2)
B	(3, 4)
C	(5, 6)

Для вычисления длины отрезка AB используется формула расстояния между двумя точками на плоскости:

d(AB) = √((x2 — x1)^2 + (y2 — y1)^2)

Подставляя значения координат вершин A и B в эту формулу, получим:

d(AB) = √((3 — 1)^2 + (4 — 2)^2) = √(2^2 + 2^2) = √8 = 2√2

Аналогично вычисляем длины отрезков BC и CA:

d(BC) = √((5 — 3)^2 + (6 — 4)^2) = √(2^2 + 2^2) = √8 = 2√2

d(CA) = √((1 — 5)^2 + (2 — 6)^2) = √((-4)^2 + (-4)^2) = √32 = 4√2

Теперь, чтобы найти длину всей ломаной, нужно просуммировать длины всех отрезков:

длина ломаной = d(AB) + d(BC) + d(CA) = 2√2 + 2√2 + 4√2 = 8√2

Таким образом, длина ломаной на координатной плоскости равна 8√2.

Значение длины ломаной в геометрии

Чтобы рассчитать длину ломаной, необходимо измерить длину каждого отрезка, из которых она состоит, и сложить эти значения. Если ломаная замкнутая, то ее длина будет равна длине замкнутого контура, то есть сумме длин всех отрезков, из которых она состоит. Если ломаная незамкнутая, то ее длина будет равна сумме длин всех отрезков, из которых она состоит, без учета последнего отрезка, который не соединяет начальную и конечную точки.

Примером ломаной может служить фигура, составленная из отрезков прямых линий, которые могут быть как прямыми, так и изогнутыми. Например, строительная схема, показывающая путь от точки А к точке Б через несколько прямых и изогнутых отрезков, представляет собой ломаную. Расчет длины такой ломаной позволяет определить протяженность пути или размер объекта, а также выполнять другие геометрические и расчетные операции.

Важно отметить, что длина ломаной зависит от выбора точек, соединяемых отрезками. При изменении положения точек или добавлении новых отрезков длина ломаной может измениться.

Свойства длины ломаной в математике

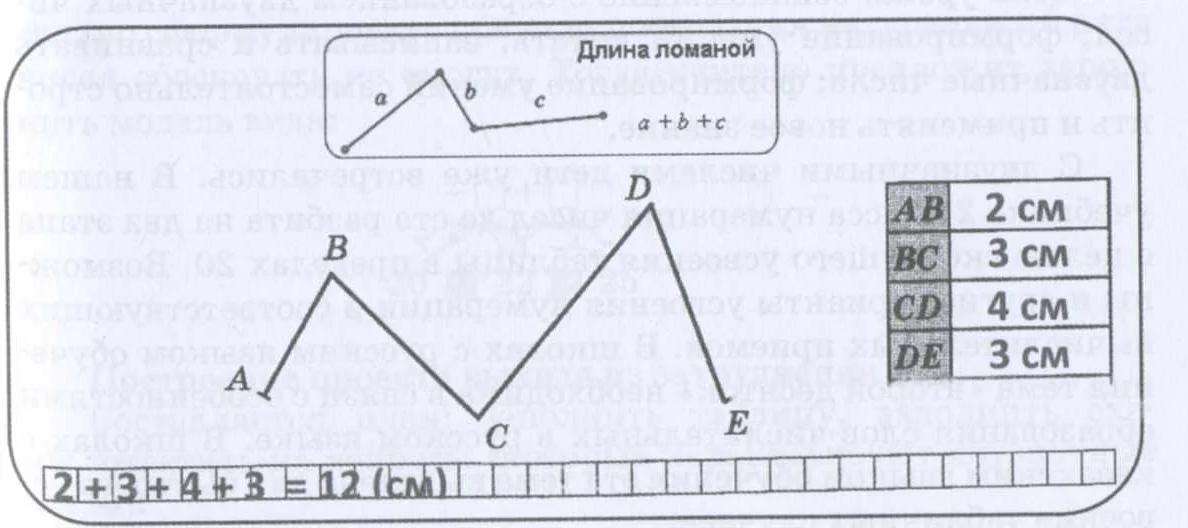
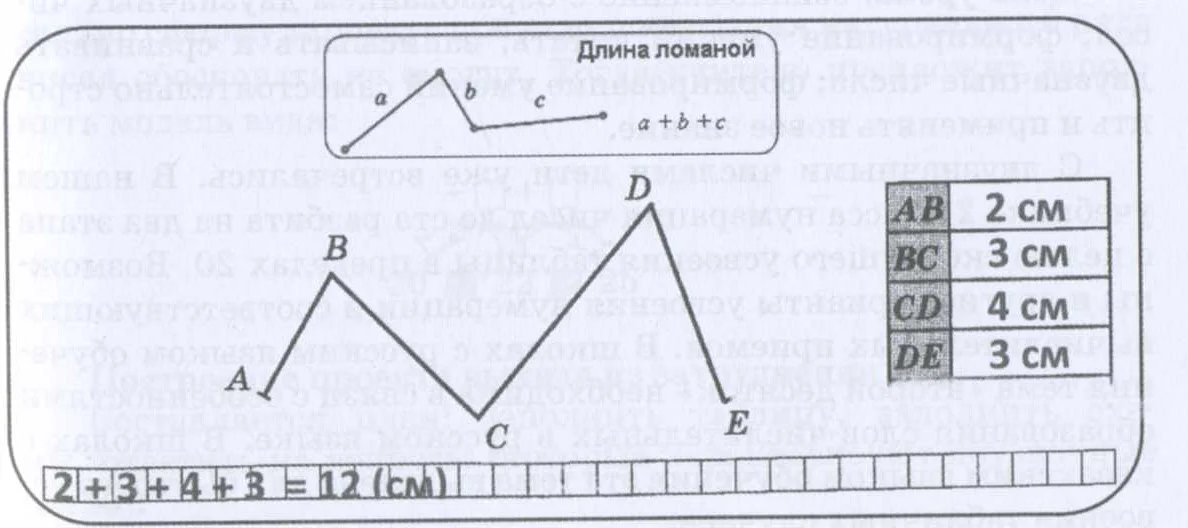
Длина ломаной в математике обладает несколькими свойствами, которые помогают нам анализировать и изучать эту характеристику геометрических фигур.

• Сумма длин отрезков: Длина ломаной равна сумме длин всех ее отрезков. Это свойство позволяет нам разбить ломаную на отдельные отрезки и вычислить их длины, а затем сложить полученные значения.
• Связь с координатами: Длину ломаной можно выразить через координаты ее вершин. Если известны координаты двух точек A(x1, y1) и B(x2, y2), то длина отрезка AB вычисляется по формуле: AB = sqrt((x2 — x1)^2 + (y2 — y1)^2).
• Неравенство треугольника: Длина ломаной, соединяющей две точки A и B, всегда меньше суммы длин отрезков AB и BC, где C — произвольная точка на ломаной. То есть, AB < AC + BC. Это свойство позволяет нам оценить, насколько ломаная «изогнута» или «завита».

Используя эти свойства, мы можем анализировать и решать различные задачи, связанные с длиной ломаной в математике.

Вопрос-ответ:

Что такое длина ломаной в математике?

Длина ломаной в математике — это сумма длин всех отрезков, из которых она состоит.

Как можно найти длину ломаной?

Для нахождения длины ломаной необходимо измерить все отрезки, из которых она состоит, и сложить их длины.

В каких единицах измеряется длина ломаной?

Длина ломаной может быть измерена в любых единицах длины, таких как метры, сантиметры, дюймы и т. д.

Можно ли привести пример ломаной и вычислить ее длину?

Да, конечно! Например, возьмем ломаную, состоящую из трех отрезков: AB = 3 см, BC = 5 см и CD = 4 см. Длина этой ломаной будет равна сумме длин отрезков: 3 + 5 + 4 = 12 см.

Может ли длина ломаной быть равна нулю?

Длина ломаной не может быть равна нулю, так как она представляет собой сумму длин отрезков, из которых она состоит. Если хотя бы один отрезок имеет ненулевую длину, то и длина ломаной будет ненулевой.

Как определить длину ломаной?

Длина ломаной в математике определяется как сумма длин всех ее отрезков.

Практическое применение длины ломаной

1. Геометрия. В геометрии длина ломаной используется для измерения длины пути между двумя точками на плоскости или в пространстве. Например, при построении дорожных карт или планировании маршрутов на них необходимо учитывать длину пути, чтобы оптимизировать время и затраты на перемещение.

2. Физика. В физике длина ломаной может использоваться для моделирования движения объекта. Например, при изучении траектории полета снаряда или движения тела в пространстве можно использовать ломаную, чтобы аппроксимировать фактическое движение и вычислить его длину.

3. Компьютерная графика. В компьютерной графике длина ломаной применяется для описания контуров и форм объектов. Например, при создании анимации или моделировании трехмерных объектов необходимо определить длину ломаной, чтобы точно воссоздать форму объекта.

4. Статистика и экономика. В статистике и экономике длина ломаной может использоваться для измерения изменения параметров во времени. Например, при анализе экономических показателей или прогнозировании временных рядов длина ломаной может помочь определить тренды и закономерности в данных.

Область примененияПример

Геометрия	Измерение длины пути на дорожной карте
Физика	Моделирование движения тела в пространстве
Компьютерная графика	Описание контуров и форм объектов
Статистика и экономика	Анализ временных рядов и трендов

Таким образом, длина ломаной является универсальным понятием, которое находит применение в различных областях науки и позволяет решать разнообразные задачи.

Видео по теме: