Что такое ломаная линия 2 класс фото в математике

Ломаная линия 2 класс фото в математике — это графическое представление, состоящее из отрезков, соединяющих точки на плоскости. На фото демонстрируется, как строить ломаную линию и использовать ее для решения задач и графического представления данных. Узнайте больше о ломаной линии 2 класс фото в математике здесь.

Ломаная линия – это геометрическая фигура, состоящая из отрезков, соединяющих последовательные точки на плоскости. В математике она изучается во втором классе и является важным элементом развития графического мышления у детей.

Чтобы нарисовать ломаную линию, необходимо провести отрезок между двумя точками, затем продолжить линию, соединив ее с третьей точкой, и так далее. Каждый отрезок называется стороной ломаной. Ломаная линия может быть открытой (концы не соединены) или замкнутой (концы соединены).

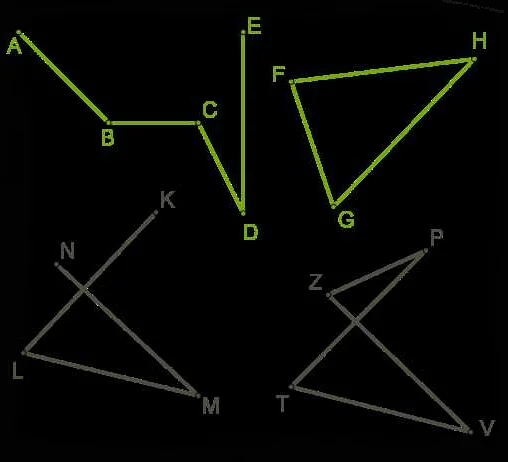
Например, для построения ломаной линии на картинке дети соединяют точки числами и буквами в указанном порядке, продолжая линию.

Ломаная линия 2 класс фото в математике

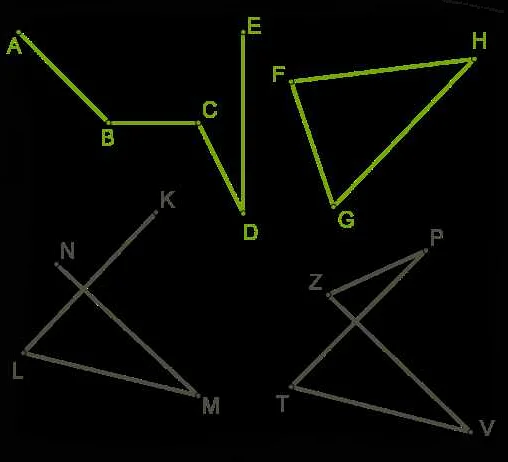
Во втором классе ученики начинают изучать ломаные линии и осваивают основные понятия связанные с ними. Они учатся определять, что такое вершина ломаной и как рисовать ломаную линию на графическом листе.

На фото вы можете увидеть пример ломаной линии, нарисованной учеником второго класса. Ломаная состоит из нескольких отрезков, соединяющих точки на графическом листе. Ученик выбрал точки, чтобы получить желаемую форму ломаной.

Изучение ломаных линий во втором классе помогает развить навыки координатной плоскости, абстрактного мышления и точности рисования. Это важные навыки, которые будут полезны в дальнейшем изучении математики.

Определение и представление

Ломаная линия второго класса — это ломаная, у которой могут быть прямолинейные участки и изгибы. Прямолинейные участки соединяются плавными изгибами. Это означает, что на каждой вершине ломаной угол между двумя звеньями не прямой.

Ломаная линия второго класса может быть представлена в виде последовательности точек, заданных координатами на плоскости, или в виде уравнения.

Точки и отрезки на ломаной линии

В математике, ломаная линия представляет собой кривую, состоящую из отрезков, соединяющих последовательные точки. Точками на ломаной линии называются концы отрезков и все внутренние точки, которые лежат на самой линии.

Отрезок на ломаной линии — это часть ломаной между двумя последовательными точками. Отрезки могут быть разной длины и наклонные, в зависимости от положения точек на ломаной. Отрезок на ломаной линии также может быть горизонтальным или вертикальным, если точки имеют одинаковую координату по одной из осей.

Когда на ломаной линии есть отрезок, который соединяет первую и последнюю точки, такая ломаная называется замкнутой. В этом случае, последняя точка является начальной точкой для следующего обхода ломаной.

Примеры точек и отрезков на ломаной линии можно видеть на рисунках и в геометрических задачах. Они могут использоваться для определения расстояний между точками, нахождения средней точки или для визуального представления данных.

Углы и направления ломаной линии

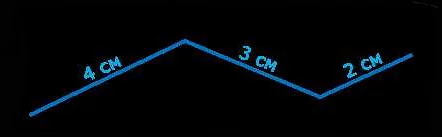
Ломаная линия в математике представляет собой прямую линию, состоящую из отрезков с разными углами между ними. Углы между соседними отрезками ломаной линии могут быть как острыми, так и тупыми.

Угол между двумя отрезками ломаной линии можно найти, используя геометрические методы. Для этого необходимо провести прямые линии, проходящие через конечные точки отрезков, и найти угол между этими линиями.

Направление ломаной линии определяется углом поворота отрезков. Если угол поворота отрезков положительный (поворот направо), то ломаная линия движется против часовой стрелки. В случае отрицательного угла поворота (поворот налево), ломаная линия движется по часовой стрелке.

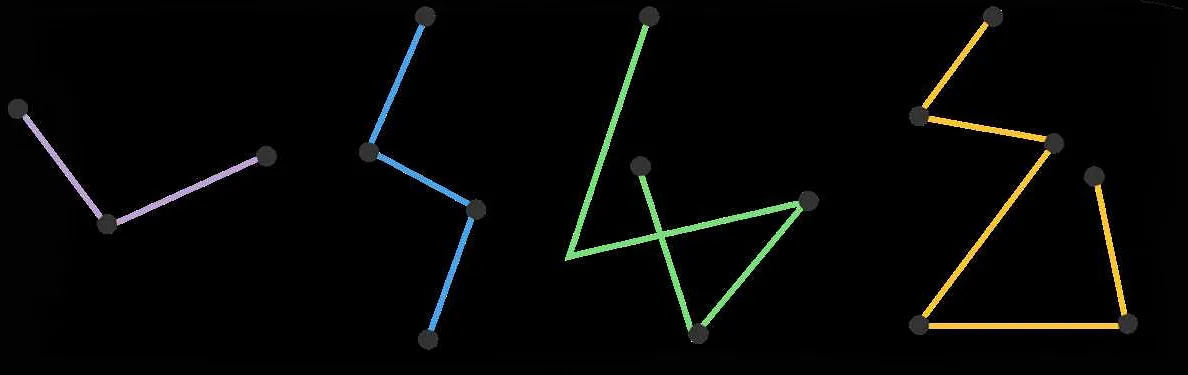
Например, на рисунке ниже показана ломаная линия, состоящая из отрезков с разными углами между ними:

Рисунок 1. Пример ломаной линии

В данном случае ломаная линия имеет два острых и два тупых угла. Также можно определить направление ломаной линии, проведя линии через конечные точки отрезков:

Рисунок 2. Направление ломаной линии

В данном примере ломаная линия имеет положительный угол поворота и движется против часовой стрелки.

Примеры ломаных линий

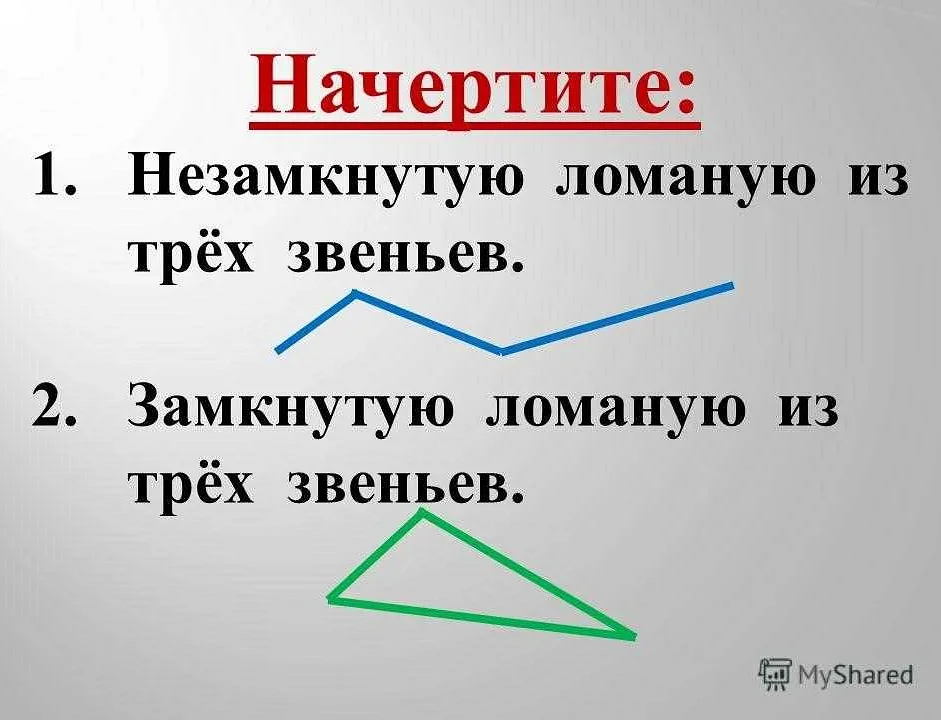
В математике ломаная линия обычно представляет собой график функции, который состоит из нескольких сегментов. Каждый сегмент соединяет две точки на плоскости. Ломаная линия может иметь различную форму и может быть использована для представления разных видов данных.

Примеры ломаных линий:

1. Прямая линия: ломаная линия, состоящая из отрезков, образующих прямой угол друг с другом. Примером может служить линия, соединяющая две точки на плоскости в прямом направлении.

2. Замкнутая ломаная линия: ломаная линия, которая начинается и заканчивается в одной и той же точке, создавая замкнутый контур. Примером может служить линия, соединяющая углы многоугольника.

3. Неправильная ломаная линия: ломаная линия, которая состоит из отрезков, не образующих прямые углы друг с другом. Примером может служить линия, соединяющая несколько точек на плоскости под разными углами.

4. Ломаная линия с пропущенными сегментами: ломаная линия, в которой некоторые сегменты отсутствуют. Примером может служить линия, соединяющая только определенные точки на плоскости.

Это лишь некоторые примеры ломаных линий, которые могут быть использованы в математике. Ломаные линии широко применяются для визуализации данных и решения различных задач в различных областях.

Свойства ломаных линий

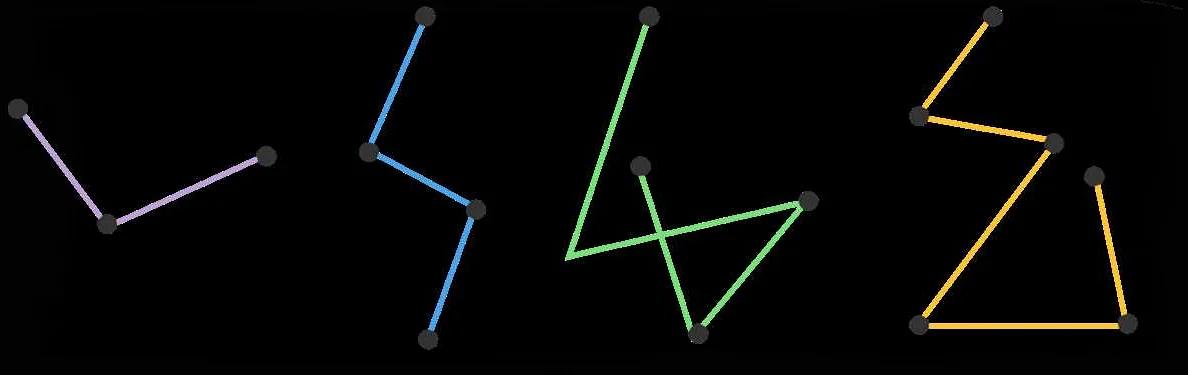
• Ломаная линия может иметь любое количество отрезков.
• Отрезки, составляющие ломаную линию, могут быть разной длины.
• Ломаная линия может быть замкнутой, то есть первая и последняя точки могут совпадать.
• Ломаная линия может быть незамкнутой, то есть первая и последняя точки не совпадают.
• У ломаной линии могут быть углы, образованные соседними отрезками. Углы могут быть острыми, прямыми или тупыми.
• Ломаная линия может иметь горизонтальные, вертикальные или наклонные отрезки.

Ломаные линии широко используются в геометрии, инженерии, архитектуре и других областях. Они помогают визуализировать и изучать различные понятия и процессы на плоскости.

Построение ломаной линии по заданным условиям

Для построения ломаной линии по заданным условиям необходимо выполнить следующие шаги:

1. Определить количество точек, через которые должна проходить ломаная линия.
2. Задать координаты каждой точки на плоскости.
3. Соединить точки с помощью отрезков, чтобы получить ломаную линию.

Пример:

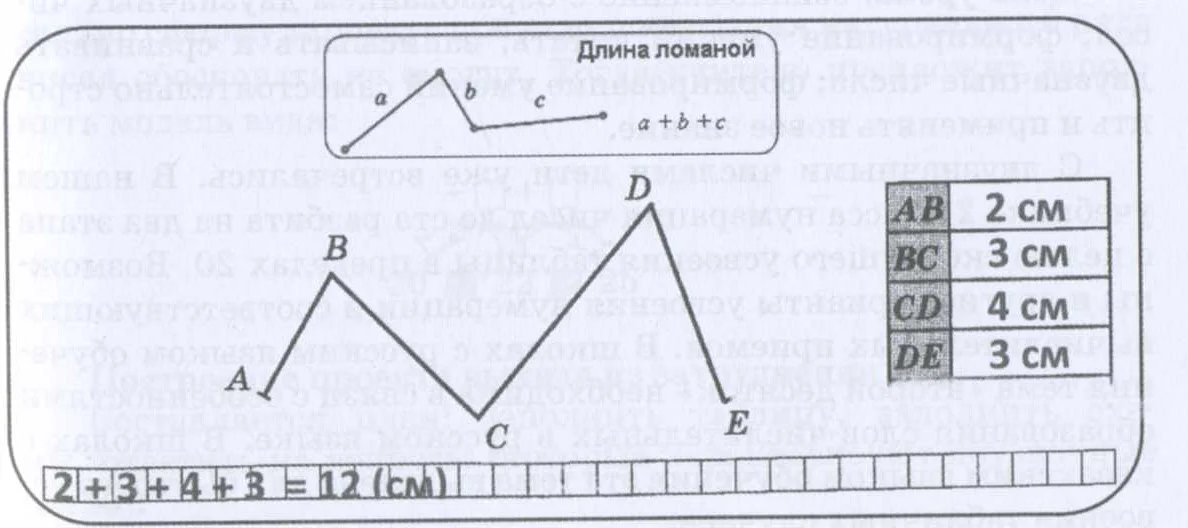
На рисунке показан пример построения ломаной линии по заданным условиям. Ломаная линия проходит через три точки: A, B и C. Координаты каждой точки заданы на плоскости. Отрезки AB и BC соединяют эти точки и образуют ломаную линию.

Таким образом, построение ломаной линии по заданным условиям позволяет визуализировать связь между точками на плоскости и создать графическое представление этой связи.

Вопрос-ответ:

Что такое ломаная линия в математике?

Ломаная линия в математике представляет собой набор отрезков, соединяющих точки на плоскости. Она может иметь любое количество отрезков и может быть как замкнутой, так и открытой.

Какие основные понятия связаны с ломаной линией?

Основные понятия, связанные с ломаной линией, включают вершины (точки, в которых отрезки пересекаются), стороны (отрезки, составляющие ломаную линию) и углы (образованные сторонами ломаной линии).

Как можно построить ломаную линию?

Для построения ломаной линии необходимо задать координаты вершин на плоскости и соединить их отрезками. Можно использовать линейку и карандаш, чтобы провести отрезки между точками.

Можно ли использовать ломаную линию для измерения расстояния?

Да, ломаная линия может использоваться для приближенного измерения расстояния между точками на плоскости. Для этого можно измерить длину каждого отрезка ломаной линии и сложить их.

Практическое применение ломаных линий

Ломаные линии имеют широкое практическое применение в различных областях, включая геометрию, графику, статистику и экономику. Ниже приведены некоторые примеры использования ломаных линий:

1. Графики и диаграммы: Ломаные линии часто используются для визуализации данных в графиках и диаграммах. Они могут представлять изменение величины во времени или отображать зависимости между различными переменными.
2. Картография: Ломаные линии используются в картографии для обозначения дорожных сетей, границ территорий, рек и других географических объектов. Они помогают визуально представить сложные маршруты и границы на карте.
3. Статистика: Ломаные линии используются для визуализации статистических данных и трендов. Они позволяют анализировать изменение величин и определять возможные зависимости между ними.
4. Инженерия: Ломаные линии используются в инженерии для проектирования и моделирования различных объектов и систем. Они помогают визуализировать и анализировать сложные структуры, пути движения и планы строительства.
5. Финансы: Ломаные линии используются в финансовой аналитике для отображения изменения цен на рынке, динамики доходов и расходов, трендов инвестиций и других финансовых показателей.

Это лишь некоторые примеры практического применения ломаных линий. Они широко используются в различных областях, где важно визуально представить данные и анализировать их связи и зависимости.

Видео по теме: