Что такое доля в математике

Доля — это математическая концепция, которая представляет собой часть от целого. Она используется для измерения относительной величины или количества и может быть выражена в виде десятичной дроби, обыкновенной дроби или процента. Узнайте, как рассчитывать долю и применять ее в различных математических задачах.

Доля — это один из основных понятий в математике, которое используется для выражения отношения одной величины к другой. Она представляет собой часть от целого, которая выражается в виде десятичной или обыкновенной дроби. Доли широко используются в различных областях, таких как финансы, процентные расчеты, статистика, и многих других.

Доли имеют свои особенности и правила использования. Для того чтобы правильно работать с долями, необходимо знать их определение и уметь проводить математические операции с ними. Например, для сложения или вычитания долей необходимо найти общий знаменатель и привести доли к общему знаменателю. Также, при умножении долей, необходимо перемножить числители и знаменатели, а при делении — умножить долю, на которую делим, на обратную долю, на которую делим.

Пример: Допустим, у нас есть 2/3 пирога. Если мы хотим узнать, сколько пирога будет составлять 1/4 от этой доли, мы можем умножить 2/3 на 1/4, что даст нам 2/12 или 1/6 пирога.

Доли также могут быть выражены в виде процентов, что позволяет более наглядно представить их значение. Например, 1/2 может быть выражено как 50% или 0.5 в десятичной форме. Процентная доля дает представление о доле величины от 100 единиц. Таким образом, доля 25% эквивалентна десятичной доле 0.25 или обыкновенной доле 1/4.

В заключение, доля — это важное понятие в математике, которое позволяет выражать отношение одной величины к другой. Операции с долями требуют знания основных правил и умения применять их в различных ситуациях. Понимание и использование долей позволит лучше разбираться в различных математических задачах и повседневных ситуациях.

Что такое доля в математике

Доля обычно выражается в виде десятичной или процентной дроби. Десятичная доля представляет собой число от 0 до 1, где 0 соответствует отсутствию данной величины, а 1 — полному наличию. Процентная доля выражается в процентах от 0% до 100%.

Например, если в классе 20 учеников, а 5 из них — девочки, то доля девочек составляет 5/20 или 0.25 в десятичном виде и 25% в процентном виде.

Доля может использоваться для решения различных задач, таких как расчеты вероятности, доли скидок, анализ статистических данных и многое другое. Понимание понятия доли является важным для успешной работы с числами и применения математических методов в различных сферах жизни.

Видео по теме:

Определение доли

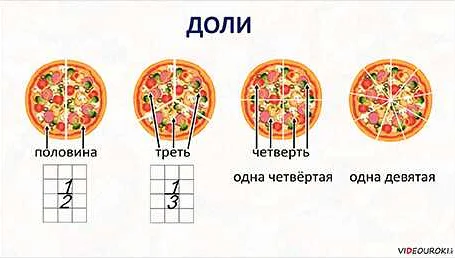
Например, если у нас есть 3 красных шара и 5 синих шаров, то доля красных шаров составляет 3/8 или 37,5% (в десятичной дроби).

Операции с долями включают сложение, вычитание, умножение и деление. Когда доли складываются или вычитаются, необходимо общий знаменатель. При умножении или делении долей, числитель и знаменатель умножаются или делятся соответственно.

Доли широко используются в финансовой отчетности, статистике, процентах, вероятности и других областях математики и науки.

Примеры доли

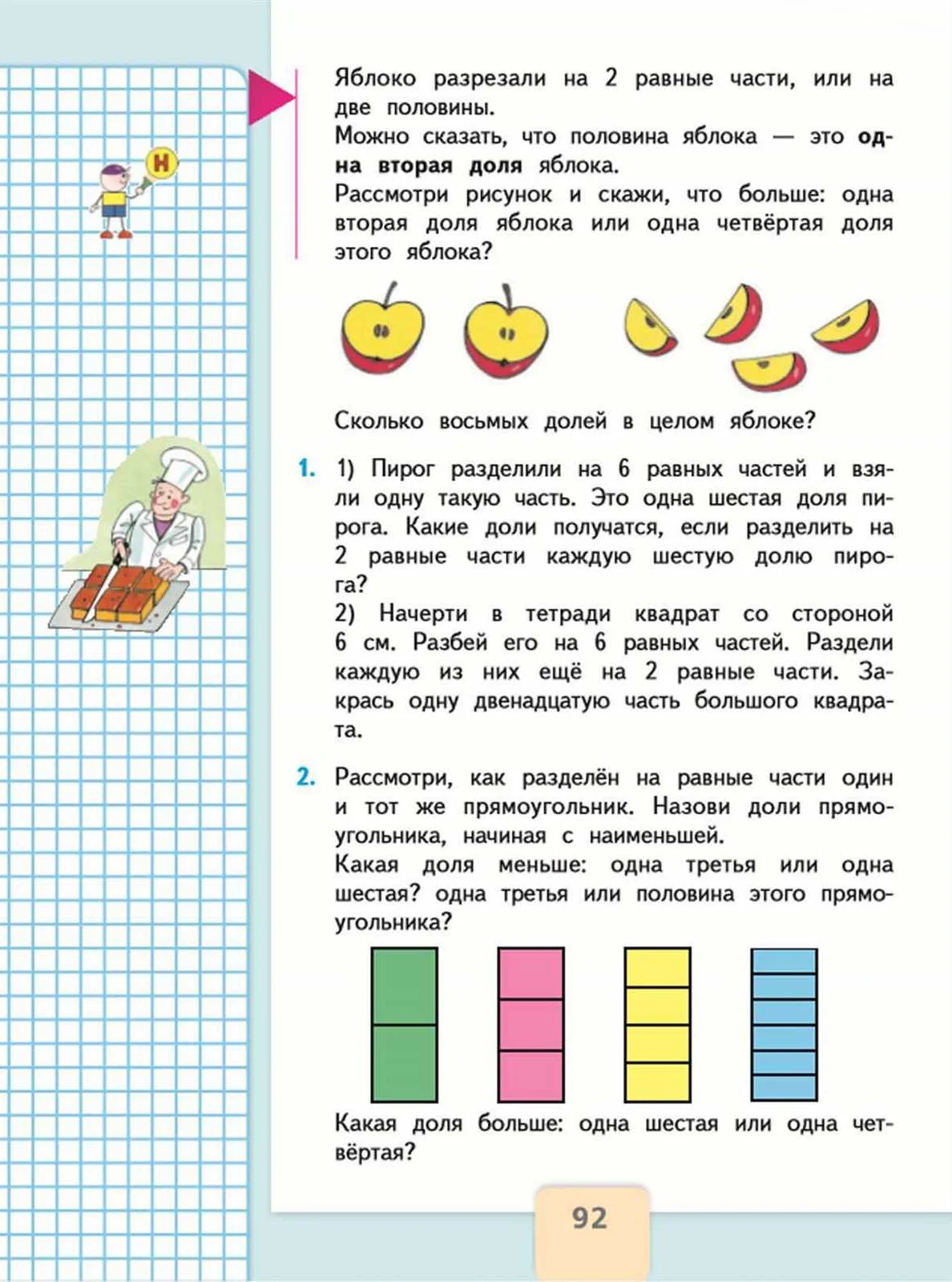
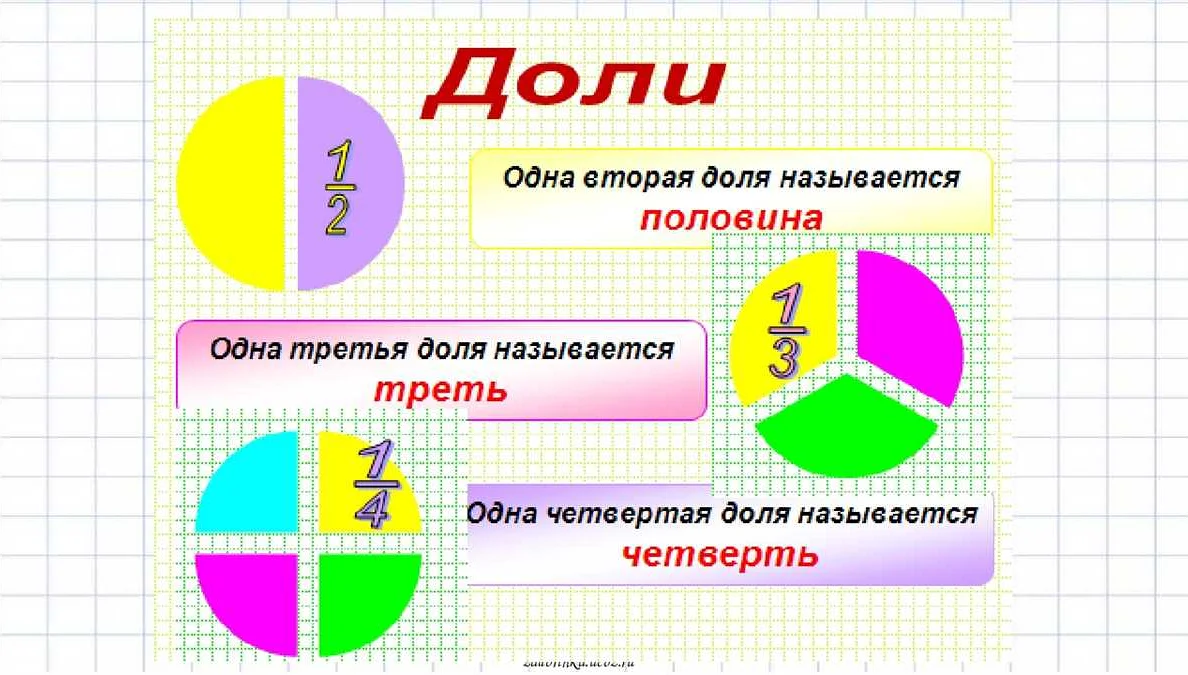
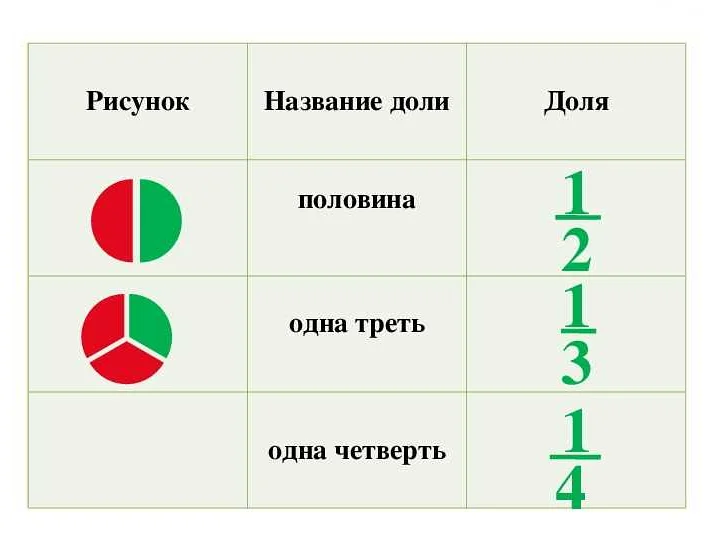
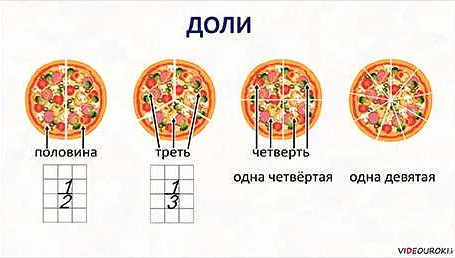
• Половина — это доля, равная одной из двух равных частей целого. Обозначается как 1/2. Например, если у нас есть пирог, то половина этого пирога — это одна из двух равных частей.
• Треть — это доля, равная одной из трех равных частей целого. Обозначается как 1/3. Например, если у нас есть пицца, то треть этой пиццы — это одна из трех равных частей.
• Четверть — это доля, равная одной из четырех равных частей целого. Обозначается как 1/4. Например, если у нас есть торт, то четверть этого торта — это одна из четырех равных частей.

Это лишь некоторые примеры долей, которые используются в математике. Доли могут быть различными и в зависимости от конкретной ситуации могут представлять разные значения.

Правила использования доли

Доля в математике представляет собой часть целого или общего количества. Доли часто используются в различных ситуациях, например, для описания процентного соотношения, расчета вероятности или разделения ресурсов.

Вот несколько правил использования доли:

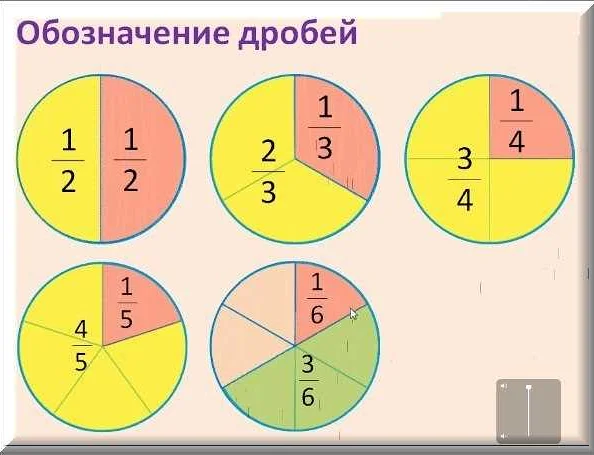
1. Доля всегда представляет собой число, записываемое в виде дроби, где числитель указывает количество частей, а знаменатель — общее количество частей. Например, доля 1/4 означает одну четверть или 25%.
2. Долю можно выразить в виде процента, умножив ее на 100. Например, доля 3/5 равна 60%.
3. Доли можно сравнивать. Если числитель одной доли больше числителя другой доли при одинаковом знаменателе, то первая доля больше второй.
4. Доли можно складывать и вычитать. Для сложения или вычитания долей знаменатели должны быть одинаковыми. Например, 1/2 + 1/3 = 5/6, а 3/4 — 1/4 = 1/2.
5. Долю можно умножать и делить. Для умножения или деления доли на число, умножайте или делите числитель. Например, (1/2) * 3 = 3/2, а (3/4) / 2 = 3/8.
6. Доли могут быть представлены в виде десятичных дробей. Для этого числитель доли делится на знаменатель. Например, 3/5 = 0,6.

Правила использования доли помогают в решении различных математических задач и позволяют работать с долями удобным и эффективным способом.

Как вычислить долю

Для вычисления доли необходимо знать два числа: числитель и знаменатель. Числитель указывает количество частей, которое необходимо выделить, а знаменатель определяет общее количество частей, на которое нужно разделить.

Чтобы вычислить долю, необходимо разделить числитель на знаменатель и умножить полученное значение на 100%. Это позволит выразить долю в процентах.

Формула для вычисления доли:

Доля = (Числитель / Знаменатель) * 100%

Например, если есть 5 красных шаров из 20, то чтобы вычислить долю красных шаров, нужно поделить 5 на 20 и умножить на 100%:

Доля красных шаров = (5 / 20) * 100% = 25%

Таким образом, доля красных шаров составляет 25% от общего количества шаров.

Вычисление доли может быть полезно для анализа данных, составления статистики и сравнения долей различных групп или явлений.

Преобразование доли в проценты

Доля представляет собой часть от целого числа. Чтобы преобразовать долю в проценты, необходимо умножить ее на 100. Это позволяет представить долю в виде процентного значения от 0% до 100%.

Для примера рассмотрим долю 3/4. Чтобы преобразовать эту долю в проценты, умножим ее на 100:

3/4 * 100 = 75%.

Таким образом, доля 3/4 равна 75%.

Также можно использовать правило трех: доля, умноженная на 100, равна проценту. Например, доля 2/5 в процентах будет равна:

2/5 * 100 = 40%.

Таким образом, доля 2/5 равна 40%.

Преобразование доли в проценты позволяет лучше представить отношение этой доли к целому числу. Это часто используется для анализа данных, статистики и представления информации в более наглядной форме.

Доля в десятичном представлении

Десятичное представление доли позволяет наглядно выразить ее долю от целого. Например, доля 1/2 будет представлена как 0.5, доля 3/4 – как 0.75.

Доли в десятичном представлении могут быть как конечными, так и бесконечными периодическими. Например, доля 1/3 будет представлена как 0.33333…, где тройка повторяется бесконечное количество раз.

Десятичное представление доли позволяет проводить арифметические операции с ней, такие как сложение, вычитание, умножение и деление. Это удобно при решении задач, связанных с долями, и позволяет получать точные результаты.

Значение доли в решении задач

Задачи, в которых требуется определить долю, встречаются в различных сферах жизни. Например, в экономике, доля может использоваться для определения процента роста или снижения продаж. В торговле, доля может использоваться для определения скидки на товар. В математике, доля может использоваться для определения вероятности наступления события в рамках вероятностной модели.

Для решения задач, связанных с долями, важно понимать основные правила и свойства. Например, при работе с процентами, долю можно выразить в виде десятичной дроби, умножив ее на 0,01. Также, при работе с долями от общей суммы, можно использовать пропорции для определения значений.

Важно помнить, что доля может быть как числом больше 1, так и числом меньше 1. Например, доля 3/4 будет равна 0,75, а доля 1/5 будет равна 0,2.

Использование долей в решении задач является неотъемлемой частью математического анализа и является одним из основных инструментов для работы с отношениями. Понимание и умение работать с долями позволяет эффективно решать задачи, связанные с различными видами отношений и процентами.

Вопрос-ответ:

Что такое доля в математике?

Доля в математике — это отношение одного числа к другому, выраженное в виде десятичной или обыкновенной дроби.

Какие примеры можно привести для понимания доли?

Примерами долей могут служить такие выражения, как «одна треть», «половина», «три четверти» и т.д. В десятичной форме это будет выглядеть как 0.33, 0.5, 0.75 соответственно.

Какие правила использования доли существуют?

При работе с долями следует помнить о некоторых правилах. Например, при сложении долей необходимо привести их к общему знаменателю. Также доли можно умножать и делить, а для этого используются соответствующие правила арифметики.

Какую роль играют доли в реальной жизни?

Доли имеют широкое применение в реальной жизни. Они используются для представления долей времени, долей вещества, долей доли и т.д. Например, если у вас есть 2 часа свободного времени и вы хотите провести половину этого времени на прогулке, то вы будете проводить 1 час на прогулке, что составляет половину от двух.

Как можно сравнить доли между собой?

Доли можно сравнивать между собой, используя различные методы. Например, можно привести доли к общему знаменателю и сравнить их числители. Также можно использовать десятичное представление долей и сравнить их значения. Например, если у нас есть доля 1/4 и доля 3/8, то мы можем сравнить их, приведя их к общему знаменателю 8/32 и 12/32, и увидеть, что 12/32 больше 8/32.

Какое определение можно дать для понятия «доля» в математике?

Доля в математике — это часть целого, выраженная в виде дроби. Она показывает, сколько частей из всего количества составляет данное значение.

Какие примеры можно привести для понимания доли в математике?

Примеры использования доли в математике включают такие задачи, как определение процента, вычисление доли от общего количества, нахождение доли в процентах и другие. Например, если у нас есть 10 яблок, а мы хотим найти долю, которую составляет 4 яблока, то ответ будет 4/10 или 0,4.