Что такое доля на математическом языке
Содержимое
- 1 Что такое доля на математическом языке
Доля — математический термин, обозначающий отношение одной величины к другой. Узнайте, какие формулы и операции используются для вычисления доли и как применять ее в решении задач.
Доля — это числовая величина, которая показывает часть целого числа или количества. В математике доля используется для выражения отношения одной величины к другой. Доли могут быть представлены в виде десятичных дробей, обыкновенных дробей или процентов.
Обычно доля выражается в виде дроби, где числитель указывает количество частей, а знаменатель — общее количество частей или целого числа. Например, если у нас есть 3 зеленых шарика и 5 красных шариков, то доля зеленых шариков будет равна 3/8.
Доли могут быть положительными или отрицательными числами. Положительные доли означают, что часть больше нуля, а отрицательные доли указывают на отсутствие части или противоположный результат.
Доля также может быть представлена в процентах, где 100% представляет полное количество или целое число. Например, если у нас есть 25 зеленых шариков и 75 красных шариков, то доля зеленых шариков будет равна 25%.
Понятие доли в математике
Доля обычно представляется в виде дроби, где числитель указывает на количество частей, а знаменатель указывает на общее количество частей. Например, если имеется 5 яблок, а 2 из них зеленые, то доля зеленых яблок составляет 2/5.
Доли также могут быть представлены в виде процентов. Например, если из 100 студентов 75 сдали экзамен, то доля студентов, сдавших экзамен, составляет 75%.
Доли могут быть использованы для сравнения и анализа данных. Например, если из 10 детей 6 предпочитают футбол, а 4 предпочитают хоккей, то можно сказать, что доля детей, предпочитающих футбол, больше, чем доля детей, предпочитающих хоккей.
ЧислительЗнаменательДоля
| 2 | 5 | 2/5 |
| 75 | 100 | 75% |
| 6 | 10 | 6/10 |
| 4 | 10 | 4/10 |
Определение доли
Доля может быть представлена в виде десятичной дроби, обыкновенной дроби или процента. Например, доля 1/4 означает, что объект разделен на четыре равные части, и одна из этих частей является долей. Доля 0.25 эквивалентна 1/4, а доля 25% также представляет 1/4.
Доли широко используются в различных областях, таких как финансы, статистика, вероятность и др. Они позволяют сравнивать и анализировать части целого и принимать решения на основе этих данных.
Например, при анализе финансовых данных доля может показывать, сколько процентов от общего дохода составляет определенная категория расходов. В статистике доля может быть использована для определения вероятности или процента встречаемости определенного события.
Числовая записьДесятичная записьОбыкновенная дробьПроцент
| 1/2 | 0.5 | 1/2 | 50% |
| 3/4 | 0.75 | 3/4 | 75% |
| 2/5 | 0.4 | 2/5 | 40% |
Примеры долей

ПримерОписание
| 1/2 | Дробь 1/2 представляет собой долю, равную одной половине целого. |
| 3/4 | Дробь 3/4 представляет собой долю, равную трем четвертям целого. |
| 2/5 | Дробь 2/5 представляет собой долю, равную двум пятых целого. |
| 0.75 | Число 0.75 также является долей, которая представляет собой три четверти целого. |
Каждая доля имеет числитель, который указывает количество частей, и знаменатель, который указывает на общее количество частей. Доли широко используются в математике, финансах, процентах и многих других областях для представления частей или долей от целого.
Как выразить долю на математическом языке
Одним из самых распространенных способов выразить долю является использование десятичной дроби. Например, если доля составляет 3/4 или 75%, то ее можно записать в виде числа 0,75.
Другой способ — использование обыкновенной дроби. Например, доля 2/5 может быть записана в виде дроби 2/5.
Также долю можно выразить с помощью процентов. Например, доля 1/2 может быть записана как 50%.
При выражении доли на математическом языке можно использовать различные математические символы и операции. Например, символ «/» используется для обозначения обыкновенной дроби, символ «%» — для обозначения процентов.
Примеры:
- Доля 1/4 можно выразить как 0,25 или 25%.
- Доля 3/7 можно выразить как 0,428571429 или 42,86%.
- Доля 2/3 можно выразить как 0,666666667 или 66,67%.
Таким образом, выражение доли на математическом языке зависит от выбранного способа записи и может быть представлено в виде десятичной, обыкновенной или процентной дроби.
Десятичная запись доли
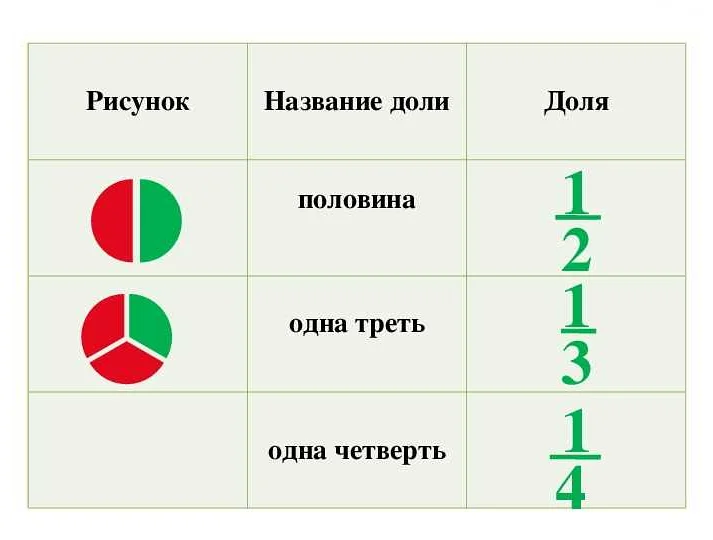
Например, доля 3/4 может быть записана в десятичной форме как 0,75. Числитель 3 стоит перед знаком дроби, а знаменатель 4 стоит после него. Чтобы получить десятичную запись доли, числитель доли необходимо разделить на знаменатель.
Другой пример — доля 1/2. Ее десятичная запись будет равна 0,5. Числитель 1 разделенный на знаменатель 2 дает результат 0,5.
Десятичная запись доли удобна для сравнения и выполнения математических операций с долями, так как позволяет представить долю в виде десятичного числа.
Процентная запись доли

Доля может быть записана в процентном виде, что позволяет легко понять, какую часть от целого она представляет. Процентная запись доли обозначается знаком процента (%) после числа, которое представляет долю.
Например, если доля составляет 3/4, то ее процентная запись будет 75%. Это означает, что данная доля представляет собой 75% от целого. Если есть доля, составляющая 1/2, то ее процентная запись будет 50%, что означает, что эта доля составляет половину или 50% от целого.
Процентная запись доли очень полезна при анализе данных и вычислениях, так как позволяет легко сравнивать доли и определить их значимость в отношении к целому.
ДоляПроцентная запись
| 1/4 | 25% |
| 1/5 | 20% |
| 3/8 | 37.5% |
Работа с долями в математических операциях

В математических операциях с долями можно выполнять различные действия, такие как сложение, вычитание, умножение и деление. Вот несколько примеров работы с долями:
- Сложение долей: чтобы сложить две доли, нужно найти общий знаменатель и сложить числители. Например, если у нас есть две доли: 3/4 и 2/5, то мы можем привести их к общему знаменателю 20 и сложить числители: 3/4 + 2/5 = 15/20 + 8/20 = 23/20.
- Вычитание долей: чтобы вычесть одну долю из другой, нужно также найти общий знаменатель и вычесть числители. Например, если у нас есть доли 5/6 и 1/3, то мы можем привести их к общему знаменателю 6 и вычесть числители: 5/6 — 1/3 = 5/6 — 2/6 = 3/6.
- Умножение долей: чтобы умножить две доли, нужно умножить числители и знаменатели. Например, если у нас есть доли 2/3 и 3/4, то мы можем умножить числители и знаменатели: 2/3 * 3/4 = 6/12 = 1/2.
- Деление долей: чтобы разделить одну долю на другую, нужно умножить первую долю на обратную второй доле. Например, если у нас есть доли 2/3 и 4/5, то мы можем разделить их: 2/3 ÷ 4/5 = 2/3 * 5/4 = 10/12 = 5/6.
Работа с долями в математических операциях является важным навыком, который помогает в решении различных задач и проблем в различных областях, таких как финансы, наука и технологии.
Сложение долей
Для сложения долей с одинаковым знаменателем достаточно сложить их числители и сохранить знаменатель. Например, если имеем две доли: 1/4 и 3/4, с общим знаменателем 4, то сумма будет равна 4/4, что равно 1.
Если же доли имеют разные знаменатели, необходимо привести их к общему знаменателю, а затем сложить числители. Например, если имеем доли: 1/3 и 1/2, то нужно привести их к общему знаменателю 6. Для первой доли получаем 2/6, а для второй — 3/6. Затем сложим числители: 2/6 + 3/6 = 5/6.
Таким образом, сложение долей требует наличия общего знаменателя и выполнения операции сложения числителей.
Пример:
Дано две доли: 2/5 и 3/5. Поскольку у них общий знаменатель 5, мы можем просто сложить их числители: 2 + 3 = 5. Получаем долю 5/5, которая равна 1.
Вычитание долей
Для выполнения вычитания долей необходимо выполнить следующие шаги:
- Сначала необходимо убедиться, что знаменатели двух долей совпадают. Если они не совпадают, необходимо привести доли к общему знаменателю.
- Затем вычитаем числители двух долей и записываем результат в числитель результирующей доли.
- Знаменатель результирующей доли остается таким же, как у исходных долей.
Например, рассмотрим вычитание долей:
Исходные долиРезультат
| 1/4 | |
| — | |
| 1/8 | |
| = | |
| 3/8 |
В данном примере мы имеем доли 1/4 и 1/8, которые имеют одинаковый знаменатель. Следовательно, мы можем вычесть числители этих долей и записать результат в числитель результирующей доли. Таким образом, получаем результат 3/8.
Умножение долей
Для умножения долей нужно умножить числитель первой доли на числитель второй доли и знаменатель первой доли на знаменатель второй доли. Полученный числитель и знаменатель новой доли будут являться произведением первых числителя и знаменателя на вторые числитель и знаменатель соответственно.
Например, умножим доли 2/3 и 7/4:
Первая доляВторая доляПроизведение
| 2/3 | 7/4 | (2 * 7)/(3 * 4) = 14/12 |
Таким образом, результатом умножения долей 2/3 и 7/4 будет доля 14/12.
Умножение долей может быть полезно в различных задачах, связанных с расчетами долей от целых чисел или величин.
Видео по теме:
Что такое доля на математическом языке?
Доля — это числовое значение, которое представляет собой отношение одного числа к другому. Обычно она записывается в виде обыкновенной дроби, где числитель указывает количество частей, а знаменатель — общее количество частей.
Как можно определить долю?
Долю можно определить, разделив одно число на другое и выразив результат в виде дроби. Например, если у вас есть 3 красных шарика и 5 синих шариков, то доля красных шариков будет равна 3/8 (три красных шарика из восьми шариков в общей сложности).
Какую информацию можно получить из доли?
Доля позволяет узнать, какую часть или долю от общего целого представляет определенное значение. Например, если у вас есть доля 3/8, это означает, что данное значение составляет 3 части из 8 возможных. Также доля может быть использована для сравнения и оценки соотношения двух значений.



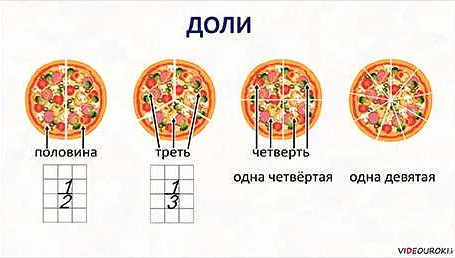

Доля, на математическом языке, представляет собой показатель, выражающий отношение одного количества к другому. Она используется для измерения и сравнения различных величин. Часто встречается в финансовой, экономической и статистической информации. Например, представим, что у меня есть 10 яблок, а у моего друга — 5 яблок. Чтобы выразить это отношение на математическом языке, мы можем использовать долю. В данном случае доля моих яблок составляет 10/15, а доля яблок друга — 5/15. Доля обычно выражается в виде десятичной или процентной формы. В нашем примере, доля моих яблок составляет 10/15 или около 0.67 в десятичной форме, а это примерно 67% в процентной форме. Доля яблок друга будет составлять 5/15 или около 0.33 в десятичной форме, что эквивалентно примерно 33% в процентной форме. Таким образом, доля позволяет нам выразить отношение одного количества к другому в более удобной форме, что облегчает сравнение и анализ данных. Это важный инструмент для понимания и использования математических концепций в повседневной жизни и на работе.
Статья очень понятно и доступно объясняет понятия доли на математическом языке. Мне нравится, что автор начинает с базового определения — доля представляет собой часть от целого. Это позволяет легко понять, что доля — это отношение объема или количества одной части к общему объему или количеству. Примеры использования доли в статье также помогают лучше усвоить материал. Они демонстрируют, как можно выразить долю в виде десятичной дроби или процента. Кроме того, автор упоминает о важности упрощения доли и предлагает методы сокращения долей, что полезно при выполнении задач. Мне особенно понравилось объяснение примера с распределением пирога между друзьями. Эта конкретная ситуация помогает визуализировать понятие доли и понять, что доля отличается от абсолютных чисел. В целом, статья очень информативная и полезная для тех, кто только начинает изучать математику или хочет освежить свои знания. Я получила полное представление о понятии доли на математическом языке и теперь легко смогу применять эту концепцию в реальной жизни. Большое спасибо автору за такую понятную статью!
Доля на математическом языке представляет собой способ выражения отношения одной величины к другой. Как женщине, мне особенно интересно понимать долю, потому что она может использоваться в самых разных ситуациях: от расчета скидки в магазине до определения вероятности события. В математике доля обычно представляется в виде числа, которое выражает соотношение между частью и целым. Например, если я имею 3 красных шара и 5 синих шаров, то доля красных шаров составляет 3/8. Это означает, что из всех шаров 3 из 8 — красные. Доли могут быть представлены в виде обыкновенных дробей или десятичных дробей. Например, доля 3/8 можно перевести в десятичную дробь — 0,375. Также доли могут быть представлены в процентах. В данном случае доля 3/8 составляет 37,5%. Понимание доли помогает в решении различных задач и принятии решений на основе данных. Например, если я хочу купить товар со скидкой 20%, я могу вычислить его стоимость, умножив исходную цену на долю 0,8. Также доли могут служить основой для определения вероятности события. Если у нас есть 4 белых шара и 6 черных шаров, мы можем вычислить вероятность достать белый шар, разделив число белых шаров на общее число шаров (4/10 или 0,4). Итак, доля на математическом языке — это способ выражения отношения одной величины к другой. Она помогает нам понять соотношение частей к целому и применять эту информацию в решении задач. Необходимость понимания доли в математике оправдана, так как она является ключевым инструментом для анализа данных и принятия решений.