Что такое движение в математике

Движение в математике — это концепция, описывающая перемещение объектов в пространстве и времени с помощью математических моделей. Узнайте, как движение определяется и изучается в математике и как его применяют в различных областях науки и техники.

В математике движение — это концепция, которая изучает перемещение объектов в пространстве. Она описывает, как объекты изменяют свои координаты во времени и пространстве. Движение является важным понятием в геометрии и физике, а также имеет применение в других областях, таких как компьютерная графика и робототехника.

Основные понятия, связанные с движением, включают траекторию, скорость и ускорение. Траектория — это путь, который объект прослеживает в пространстве. Она может быть прямой, кривой или закрытой. Скорость — это изменение позиции объекта по времени. Она может быть постоянной или меняться во времени. Ускорение — это изменение скорости объекта по времени.

Примеры движения могут включать движение автомобиля по дороге, движение планет вокруг Солнца и движение маятника. В каждом из этих примеров объекты изменяют свои координаты во времени и пространстве.

Изучение движения позволяет математикам и физикам моделировать и предсказывать поведение объектов в пространстве. Оно также имеет практическое применение в различных областях науки и технологий. Понимание понятий и принципов движения является важным для развития научных и инженерных решений, а также для понимания природы окружающего мира.

Определение движения в математике

Движение может быть задано с помощью двух основных понятий: трансляции и поворота.

Трансляция — это перемещение объекта или фигуры на определенное расстояние в определенном направлении без изменения формы и размеров.

Поворот — это изменение ориентации объекта или фигуры относительно определенной точки, называемой центром поворота. Поворот может быть задан углом и направлением.

Движение также может быть комбинацией трансляции и поворота. Например, объект может быть сначала передвинут на определенное расстояние, а затем повернут относительно центра поворота.

Определение движения в математике играет важную роль в геометрии и механике, а также в решении задач, связанных с перемещением объектов и фигур.

Понятие траектории в движении

Траектория определяется положением объекта в каждый момент времени. Например, если мы рассматриваем движение автомобиля, то его траектория будет представлять собой линию, соединяющую все положения автомобиля в разные моменты времени.

Траектория может быть задана как аналитически, используя уравнения, так и геометрически, с помощью графического представления.

Примерами траекторий могут служить:

• Прямая линия, которую описывает птица при полете на большой высоте.
• Окружность, по которой движется колесо велосипеда.
• Зигзагообразная линия, по которой движется муравей по поверхности земли.

Знание траектории движения объекта позволяет анализировать его движение, вычислять скорости и ускорения, предсказывать его положение в будущем и многое другое.

Определение скорости в движении

Скорость может быть представлена как скалярная величина, которая указывает на величину перемещения объекта, либо как векторная величина, которая указывает на величину перемещения и его направление.

Для определения скорости в движении необходимо знать пройденное расстояние и затраченное время. Скорость вычисляется по формуле:

скорость = пройденное расстояние / затраченное время

Например, если объект пройдет расстояние 100 метров за 10 секунд, то его скорость будет равна 10 метров в секунду.

Скорость может быть постоянной, если объект движется с постоянной скоростью, либо переменной, если скорость изменяется со временем. Также важно отметить, что скорость может быть положительной (при движении вперед) или отрицательной (при движении назад).

Понятие ускорения в движении

Ускорение может быть положительным, если скорость тела увеличивается, отрицательным, если скорость уменьшается, или нулевым, если скорость не изменяется.

Ускорение можно выразить формулой:

а = (v — u) / t

где а – ускорение, v – конечная скорость, u – начальная скорость и t – время.

Примеры ускоренного движения включают падение свободного тела под действием силы тяжести, движение автомобиля при разгоне или торможении, а также движение планет вокруг Солнца.

Примеры движения в математике

В математике существуют различные примеры движения, которые могут быть представлены в виде преобразований геометрических фигур.

Один из примеров движения — это сдвиг. Сдвиг представляет собой перемещение фигуры без изменения ее формы и размеров. Например, если мы возьмем квадрат и сдвинем его на некоторое расстояние вправо, то получим новое положение квадрата, но его стороны и углы останутся неизменными.

Еще одним примером движения является поворот. Поворот представляет собой вращение фигуры относительно некоторой точки на заданный угол. Например, если мы возьмем треугольник и повернем его относительно одной из его вершин на 90 градусов, то получим новое положение треугольника, но его стороны и углы также останутся неизменными.

Также движение может быть отражением. Отражение представляет собой отражение фигуры относительно некоторой прямой. Например, если мы возьмем прямоугольник и отразим его относительно горизонтальной прямой, то получим новое положение прямоугольника, но его стороны и углы будут отражены по отношению к исходной фигуре.

Это лишь некоторые примеры движений в математике. Благодаря этим преобразованиям геометрических фигур мы можем изучать и анализировать их свойства и отношения.

Движение прямолинейное и криволинейное

Прямолинейное движение – это движение объекта по прямой линии. Примером прямолинейного движения может служить движение автомобиля по прямой дороге без поворотов или движение тела, брошенного вертикально вверх или вниз. В прямолинейном движении объект перемещается вдоль одного направления, не изменяя своего направления движения.

Криволинейное движение – это движение объекта по кривой линии. Примером криволинейного движения может служить движение автомобиля по изогнутой дороге или движение спутника вокруг Земли. В криволинейном движении объект меняет направление движения, следуя по изогнутой траектории.

Для описания движения объектов в математике применяются различные понятия и методы, такие как скорость, ускорение, траектория и время. Изучение движения позволяет предсказывать и объяснять различные физические явления и процессы, а также решать задачи, связанные с перемещением объектов.

Видео по теме:

Вопрос-ответ:

Что такое движение в математике?

В математике движение — это перемещение объекта по пространству без изменения его формы или размеров.

Какие основные понятия связаны с движением в математике?

Основными понятиями, связанными с движением в математике, являются траектория, скорость, ускорение и время.

Как можно описать движение математически?

Движение может быть описано математически с помощью функций, где время является независимой переменной, а координаты объекта — зависимыми переменными. Например, можно использовать функцию x(t) для описания координаты x в зависимости от времени t.

Какие есть примеры движения в математике?

Примеры движения в математике включают движение по прямой линии, круговое движение, движение по эллипсу, параллельное перемещение и повороты в пространстве.

Какие характеристики движения можно измерить в математике?

В математике можно измерить различные характеристики движения, такие как скорость, ускорение, время, пройденное расстояние и изменение положения объекта.

Что такое движение в математике?

Движение в математике — это преобразование, которое меняет положение объекта в пространстве без изменения его формы и размеров.

Какие основные понятия связаны с движением в математике?

Основные понятия, связанные с движением в математике, включают: трансляцию, поворот и отражение. Трансляция перемещает объект параллельно определенному направлению, поворот вращает объект вокруг определенной точки, а отражение отображает объект относительно определенной оси.

Относительное движение в математике

В математике относительное движение обычно представляется с помощью векторов. Для описания движения вектором необходимо указать его направление, длину и точку приложения. При сравнении движения двух объектов, их векторы можно сложить или вычитать, чтобы получить вектор относительного движения.

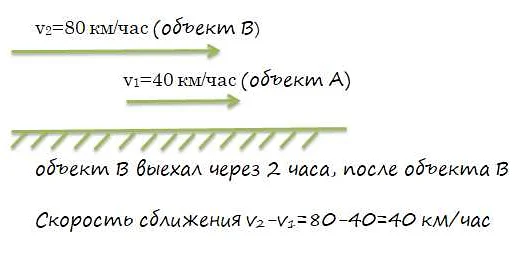
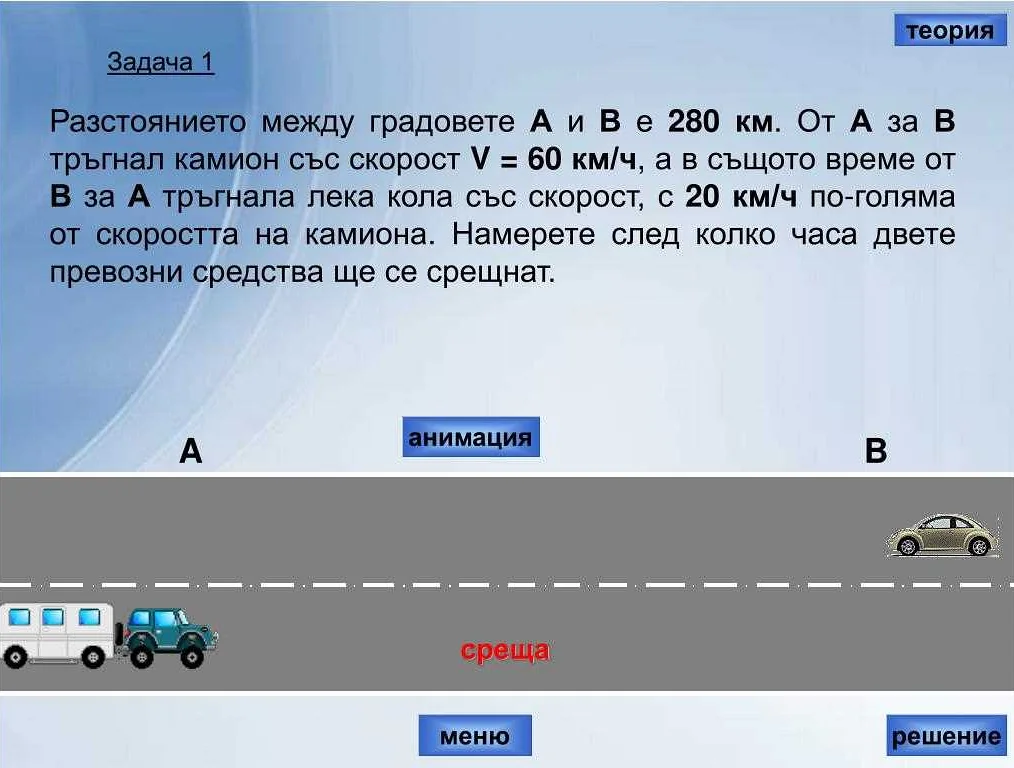
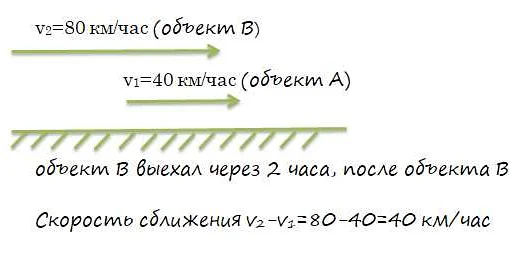
Примером относительного движения может служить движение двух автомобилей на дороге. Если один автомобиль движется со скоростью 60 км/ч, а другой автомобиль движется со скоростью 80 км/ч, то относительная скорость одного автомобиля относительно другого будет равна разности их скоростей, то есть 80 км/ч — 60 км/ч = 20 км/ч.

Относительное движение играет важную роль в решении различных задач, связанных с движением объектов и определением их скоростей и ускорений. Понимание этого понятия позволяет более точно описывать и анализировать движение объектов в различных ситуациях.

ОпределениеПример

Относительное движение	Два поезда движутся в одном направлении с разными скоростями
Относительная скорость	Скорость самолета относительно земли
Относительное ускорение	Ускорение автомобиля относительно велосипеда

Графическое представление движения

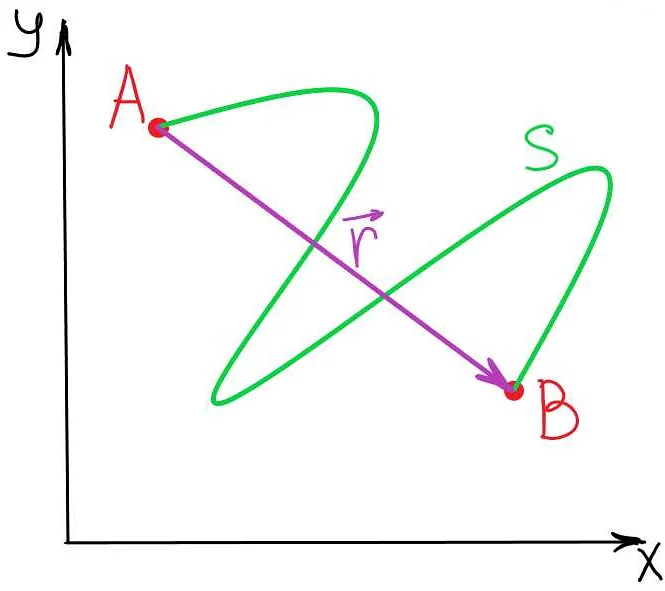
Для графического представления движения используются различные графические элементы, такие как стрелки, линии, диаграммы и др. Они помогают отобразить начальное и конечное положение объекта, его траекторию и направление движения.

Примеры графического представления движения:

1. Для представления прямолинейного движения вдоль оси используются стрелки, направленные вдоль оси противоположно друг другу. Начальное положение объекта обозначается одной стрелкой, а конечное – другой стрелкой, которая может быть направлена в противоположную сторону.

2. Для представления движения по окружности используется диаграмма, на которой отображается начальное положение объекта на окружности и его последующее перемещение вдоль нее.

3. Для представления сложного движения в пространстве, например, движения тела по плоскости или в трехмерном пространстве, используются системы координат, на которых отображается начальное и конечное положение объекта, его траектория и направление движения.

Графическое представление движения является важным инструментом в математике и физике, позволяющим лучше понять и визуализировать различные аспекты движения объектов.