Что такое ме в математике

Ме (Mе) – это математическое понятие, обозначающее максимальное элементарное множество. В математике оно используется при рассмотрении теории множеств и множественной алгебры. Узнайте, что такое Ме и как его применяют в математике.

Математика — это наука, которая изучает структуру, свойства и отношения чисел, пространства, структуру изменений и фундаментальные законы, объединяющие все эти объекты. В математике существует множество констант, которые играют важную роль в различных областях этой науки. Одной из таких констант является число «е».

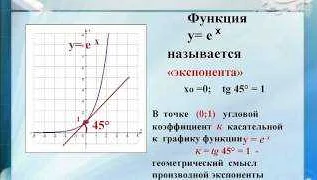
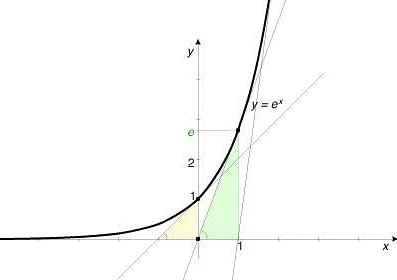
Число «е» (экспонента) является одной из математических констант и является основанием натурального логарифма. Оно приближенно равно 2,71828, но его значение может быть расчитано с большей точностью. Число «е» играет важную роль в различных областях математики, физики и других наук.

Одно из наиболее известных применений числа «е» — в формуле для вычисления непрерывного процента. Формула имеет вид P(t) = P(0) * e^(rt), где P(t) — конечная сумма, P(0) — начальная сумма, r — процентная ставка, t — время в годах. Число «е» также встречается в других областях математики, таких как комплексный анализ, дифференциальные уравнения и статистика.

Изучение числа «е» позволяет получить более глубокое понимание математических концепций и применить их в различных областях науки и техники. Это число является одним из фундаментальных элементов математической теории и позволяет увидеть связь между различными математическими конструкциями.

Таким образом, число «е» является важной константой в математике и науке в целом. Оно играет значительную роль в различных областях и позволяет лучше понять и объяснить многочисленные явления и закономерности. Осознание значения числа «е» поможет исследователям и ученым более эффективно применять математические методы и концепции в своей работе.

Определение понятия «е» в математике

Число «е» может быть определено как предел суммы (1 + 1/n)^n, когда число «n» стремится к бесконечности. Это число появляется во многих разделах математики, физики и других науках и имеет множество применений, как в теории вероятностей, так и в теории чисел.

Особенностью числа «е» является то, что оно является иррациональным и трансцендентным числом, что означает, что его десятичная запись не имеет периодической структуры и не может быть выражена в виде дроби. Это число также имеет много интересных свойств и взаимосвязей с другими математическими константами, такими как число «π» и комплексные числа.

Число «е» имеет большое значение в приложениях, связанных с ростом и изменением. Оно играет важную роль в моделировании процессов роста, децимации и экспоненциального упадка. Также оно является основой для расчетов процентных ставок, алгоритмов в финансовой математике и других областях.

Математическая константа «е» и ее значение

Значение «е» возникает из рассмотрения предела функции (1 + 1/n)^n при n, стремящемся к бесконечности. Это число является основой экспоненциальной функции и имеет множество важных применений в различных областях математики и физики.

Одно из наиболее известных применений «е» — это формула для вычисления сложного процента: A = P * (1 + r/n)^(n*t), где A — конечная сумма, P — начальная сумма, r — годовая процентная ставка, n — количество периодов в году, t — число лет. В этой формуле «е» используется для приближения бесконечно малых изменений.

Математическая константа «е» также широко применяется в теории вероятностей, дифференциальном и интегральном исчислении, комплексном анализе и многих других областях математики. Ее значение часто возникает в задачах, связанных с ростом и изменениями величин.

Значение «е» имеет особую важность в математике и является одной из ключевых констант, которая помогает в понимании и решении различных задач и проблем, связанных с изменениями и ростом.

Происхождение символа «е» в математике

Происхождение символа «е» в математике связано с работы швейцарского математика Леонарда Эйлера. В 1731 году он использовал первую букву имени Йоханна Бернулли, друга и коллеги, для обозначения этой константы. С течением времени буква «е» стала широко принятой и используется во многих математических текстах и учебниках.

Символ «е» имеет множество применений в математике, особенно в области экспоненциальных и логарифмических функций. Он встречается в формулах и уравнениях, а также в различных областях науки, где используется математическое моделирование.

Примеры использования символа «е» в математике:

Уравнение экспоненты: \(e^x\)

Формула натурального логарифма: \(\ln(x)\)

Уравнение роста с постоянной скоростью: \(P = P_0 \cdot e^{rt}\)

Использование символа «е» в математике позволяет удобно и компактно записывать различные математические формулы и выражения, а также облегчает проведение различных вычислений.

Понятие «е» в различных математических областях

Число «е» имеет особое значение в различных математических областях. Вот несколько примеров, где «е» играет важную роль:

ОбластьОписание

Математический анализ	В математическом анализе число «е» является основой натурального логарифма и экспоненциальной функции. Например, экспонента e^x определяется как сумма бесконечного ряда 1 + x + x^2/2! + x^3/3! + …
Теория вероятностей	В теории вероятностей число «е» используется в формуле для вычисления непрерывного распределения вероятностей. Это связано с тем, что «е» является основанием натурального логарифма, который является базисом для многих распределений.
Комплексный анализ	В комплексном анализе число «е» играет важную роль в формуле Эйлера, связывающей мнимую единицу i, число «е» и тригонометрические функции. Формула Эйлера имеет вид e^(iθ) = cos(θ) + i*sin(θ), где θ — угол в радианах.

Это лишь несколько примеров, как число «е» используется в различных математических областях. Его уникальные свойства делают его незаменимым инструментом для решения различных задач и формул в математике.

Использование «е» в теории вероятностей

В теории вероятностей символ «е» часто используется для обозначения базовой константы, которая называется числом Эйлера или числом Непера. Это иррациональное число, которое приближенно равно 2,71828.

Число «е» широко применяется в формулах вероятности и статистики. Оно используется, например, в формуле для вычисления непрерывной производительности в экспоненциальном распределении.

Также число «е» используется в формуле для вычисления производящей функции моментов, которая играет важную роль в теории вероятностей.

Понимание и использование числа «е» в теории вероятностей является необходимым для работы с математическими моделями и анализом случайных явлений.

Роль «е» в математическом анализе и дифференциальных уравнениях

В математическом анализе «е» является одним из ключевых чисел. Оно определяет экспоненциальную функцию, которая имеет особые свойства. Экспоненциальная функция с основанием «е» имеет производную, равную самой функции. Это означает, что график этой функции имеет уникальную форму и может использоваться для моделирования различных явлений, таких как рост популяции или распад вещества.

В дифференциальных уравнениях «е» также играет важную роль. Дифференциальные уравнения описывают зависимость изменения величины от ее производной. Многие дифференциальные уравнения имеют решения, в которых встречается число «е». Например, решение дифференциального уравнения, описывающего экспоненциальный рост, будет содержать «е» в своей формуле.

Также число «е» широко используется в различных областях математики, физики и инженерии. Оно встречается в формулах, описывающих гармонические колебания, вероятность, статистику, электромагнетизм и многие другие явления. Благодаря своим уникальным свойствам, «е» играет важную роль в понимании и решении различных математических и физических задач.

Значение «е» в комплексном анализе и теории функций

Одним из ключевых свойств числа «е» является его экспоненциальное представление. В комплексном анализе, экспонента с базой «е» определяется следующим образом:

База «е»Комплексное числоЭкспонента

«е»

z

ez

Это представление позволяет использовать экспоненту с базой «е» для анализа и решения различных задач в комплексном анализе и теории функций. Например, она играет важную роль в решении дифференциальных уравнений и интегралов с помощью методов комплексного анализа.

Кроме того, число «е» также связано с тригонометрическими функциями через формулу Эйлера:

Формула ЭйлераЭкспонентаКосинусСинус

eiz = cos(z) + i*sin(z)

eiz

cos(z)

sin(z)

Эта формула связывает экспоненту с базой «е» с тригонометрическими функциями и позволяет использовать их в комплексном анализе для анализа и решения различных задач.

Таким образом, число «е» играет важную роль в комплексном анализе и теории функций, позволяя решать различные задачи и проводить анализ функций с помощью экспоненты и тригонометрических функций.

Примеры использования «е» в математике

2. Формула комплексного числа, имеющая вид z = x + yi, где x и y — вещественные числа, а i — мнимая единица. Мнимая единица i определяется как i^2 = -1 и используется для работы с комплексными числами. Комплексные числа широко применяются в математическом анализе, электротехнике, физике и других областях науки.

3. Ряд Тейлора — это представление функции в виде бесконечной суммы степеней x, где x — переменная, а коэффициенты ряда зависят от значения функции и ее производных в некоторой точке. Ряд Тейлора позволяет приближенно вычислять значение функции вблизи этой точки. Например, ряд Тейлора для функции e^x имеет вид e^x = 1 + x + (x^2)/2! + (x^3)/3! + … и используется для приближенных расчетов и аппроксимаций в различных областях математики и физики.

4. Число е встречается в формуле для вычисления сложного процента (процентных ставок) в финансовых расчетах. Формула имеет вид A = P(1 + r/n)^(nt), где A — конечная сумма денег, P — начальная сумма денег, r — годовая процентная ставка, n — количество периодов в году, t — общее количество лет. Значение числа е используется при вычислении сложного процента, когда количество периодов n стремится к бесконечности.

5. В математической статистике число е используется в формуле для вычисления математического ожидания и дисперсии равномерного распределения. Значение математического ожидания M и дисперсии D определяются как M = (a + b) / 2 и D = (b — a)^2 / 12, где a и b — границы интервала равномерного распределения. При использовании формулы для расчета математического ожидания и дисперсии равномерного распределения число е встречается в вычислениях.

Формула для вычисления процентной ставки с использованием «е»

Формула для вычисления процентной ставки с использованием «е» выглядит следующим образом:

Процентная ставка = (1 — (1 + i)-n) * 100%

где:

• Процентная ставка — искомая величина, выраженная в процентах;
• i — годовая процентная ставка, выраженная в виде десятичной дроби (например, 0,05 для 5%);
• n — количество периодов (например, количество лет).

В данной формуле, число «е» используется для выражения экспоненциально нарастающего процента. Оно возводится в степень, равную произведению годовой процентной ставки и количества периодов.

Использование числа «е» в формуле для вычисления процентной ставки позволяет учесть сложные процентные расчеты, связанные с накоплением процентов на протяжении определенного периода времени.

Интегралы с «е» в основании

Если в интеграле встречается «е» в основании, то его вычисление требует использования специальных методов и подходов. Как правило, для вычисления таких интегралов используется замена переменных или применение определенных формул и свойств.

Примером интеграла с «е» в основании может служить следующий интеграл:

ИнтегралВыражение

∫ e^x dx

e^x + C

В данном примере, интеграл ∫ e^x dx означает нахождение функции, производная которой равна e^x. Результатом вычисления данного интеграла является функция e^x + C, где C — произвольная постоянная.

Интегралы с «е» в основании широко применяются в различных областях математики, физики, экономики и других наук. Знание методов и подходов к вычислению таких интегралов позволяет решать сложные задачи и находить точные решения в различных приложениях.

Вопрос-ответ:

Зачем нужна буква «е» в математике?

Буква «е» в математике используется для обозначения основания натурального логарифма. Также она используется в некоторых математических формулах и уравнениях.

Как определить значение «е»?

Значение числа «е» равно примерно 2.71828. Оно является иррациональным числом, то есть не может быть точно представлено десятичной дробью или конечной десятичной дробью.

Какая формула используется для вычисления «е»?

Число «е» может быть вычислено с помощью формулы: е = (1 + 1/n)^n, где n — бесконечно большое число.

Какие примеры использования числа «е» в математике?

Число «е» широко используется в различных областях математики. Например, оно встречается в формуле для вычисления непрерывного процента, в модели роста популяции, в теории вероятностей и в других математических моделях.

Можно ли использовать другую букву вместо «е» для обозначения основания натурального логарифма?

В математике обычно используется буква «е» для обозначения основания натурального логарифма. Однако в некоторых случаях могут быть использованы и другие обозначения, например, «ln» или «log».

Что означает символ «е» в математике?

Символ «е» в математике используется для обозначения основания натурального логарифма, которое примерно равно 2.71828. Это число встречается во многих математических формулах и имеет много важных свойств.

Видео по теме: