Что такое экспонента в математике простыми словами

Экспонента — это математическая функция, которая описывает рост или убывание некоторой величины со временем. Она имеет свойства экспоненциального роста и позволяет моделировать различные явления в физике, экономике и других областях. В данной статье мы рассмотрим, что такое экспонента и как ее можно использовать для решения различных задач.

В математике существует множество понятий, которые могут вызвать затруднение в понимании. Одним из таких понятий является экспонента. Что же это такое? Экспонента — это математическая функция, которая описывает рост или убывание величины с фиксированным коэффициентом.

Основой экспоненты является число e, которое приближено равно 2,71828. Это число играет важную роль во многих областях науки и естествознания. Оно постоянно встречается в формулах, описывающих рост и изменение величин.

Функция экспоненты обладает следующим свойством: при увеличении аргумента на единицу, значение функции увеличивается в e раз. Например, если мы возьмем экспоненту от единицы, то получим число e. А если мы возьмем экспоненту от двойки, то получим число e в квадрате, то есть e^2.

Экспонента является мощным инструментом для описания роста и изменения величин. Она используется в финансовой математике, физике, экономике и других научных дисциплинах. Понимание этого понятия поможет разобраться во многих сложных задачах и является неотъемлемой частью математической грамотности.

Определение экспоненты

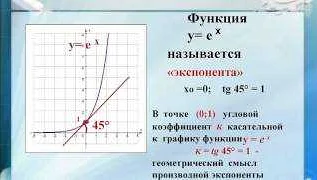
Экспонента обозначается символом «e» и может быть записана в виде e^x, где «x» — это показатель степени. Значение экспоненты увеличивается экспоненциально с ростом показателя степени: чем больше значение «x», тем больше значение экспоненты. Например, если x = 2, то e^2 = 7.389, а если x = 3, то e^3 = 20.086.

Экспонента широко применяется в различных областях науки и инженерии, таких как физика, экономика, биология и т.д. Она помогает моделировать и описывать процессы, которые характеризуются быстрым ростом или убыванием.

Свойства экспоненты

Экспонента обладает несколькими важными свойствами, которые помогают решать различные задачи и упрощать вычисления.

1. Сложение экспонент: Когда складываются две экспоненты с одинаковым основанием, результатом будет экспонента с тем же основанием, а показатель будет равен сумме показателей. Например, ax + ay = ax+y.

2. Умножение экспонент: При умножении двух экспонент с одинаковым основанием, результатом будет экспонента с тем же основанием, а показатель будет равен сумме показателей. Например, ax * ay = ax+y.

3. Возведение экспоненты в степень: Если экспонента возводится в степень, то показатель умножается на эту степень. Например, (ax)y = axy.

4. Деление экспонент: При делении двух экспонент с одинаковым основанием, результатом будет экспонента с тем же основанием, а показатель будет равен разности показателей. Например, ax / ay = ax-y.

5. Возведение в нулевую степень: Любое число, кроме нуля, возводится в нулевую степень равно единице. Например, a0 = 1.

6. Возведение в отрицательную степень: Число, возведенное в отрицательную степень, становится обратным к числу, возведенному в положительную степень с тем же основанием. Например, a-x = 1 / ax.

Эти свойства экспоненты позволяют упрощать выражения и решать сложные задачи, связанные с экспонентами.

Формула экспоненты

e

x

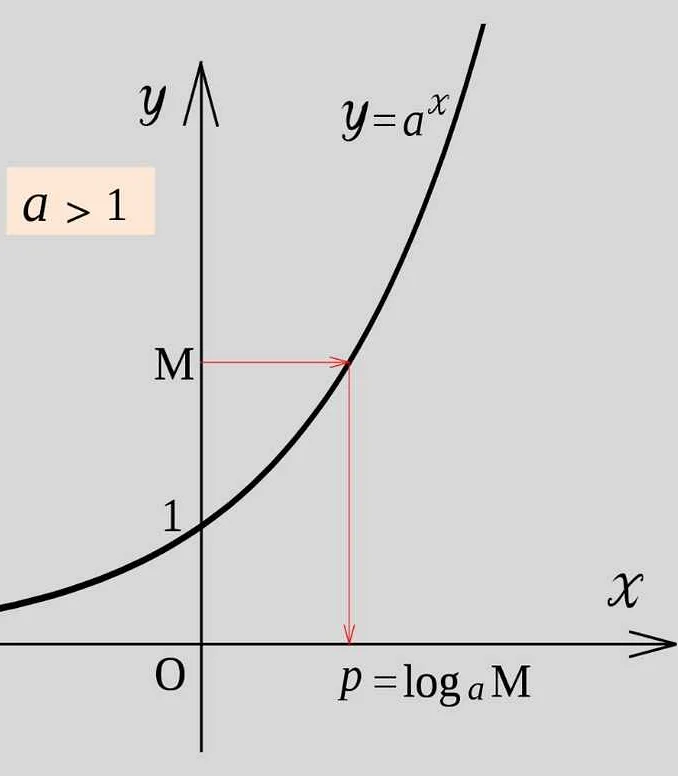
Здесь e – основание экспоненты, которое примерно равно 2.71828, а x – показатель степени, который определяет, насколько величина увеличивается или уменьшается.

Формула экспоненты позволяет нам вычислять значения функции для различных значений показателя степени. Например, если x равно 2, то значение экспоненты будет:

e

2

Результатом этого выражения будет число, примерно равное 7.38906. Таким образом, экспонента позволяет нам вычислять значения функции для разных значений показателя степени и увидеть, как величина меняется в зависимости от этого параметра.

Формула экспоненты также имеет много интересных математических свойств и применений. Она широко используется в различных научных и инженерных областях, таких как физика, экономика и статистика, и играет важную роль в моделировании и прогнозировании различных явлений.

Примеры использования экспоненты

Экспонента широко используется в различных областях математики и науки. Ниже приведены несколько примеров ее применения:

• Финансовая математика: экспонента используется для моделирования процентных ставок, роста населения и инфляции.
• Физика: законы, описывающие затухание колебаний, распределение радиоактивного распада и температуру расплавленного тела, также включают экспоненту.
• Статистика: экспоненциальное распределение используется для описания времени между столкновениями частиц в физике высоких энергий или времени между появлениями событий в теории надежности.
• Компьютерная графика: экспонентные функции используются для создания плавных анимаций и эффектов перехода.

Эти примеры демонстрируют, как экспонента помогает моделировать различные явления и взаимодействия в математике и науке.

Экспонента и проценты

Одно из важных применений экспоненты связано с процентами. Проценты — это способ представления доли числа в сотых долях. Например, 50 процентов равно 0,5, а 100 процентов равно 1.

Связь экспоненты и процентов выражается через формулу роста или убывания с постоянной процентной ставкой. Если начальная сумма равна S, а временной период — t, то конечная сумма будет равна S * (1 + r/100)^t, где r — процентная ставка.

Например, если у вас есть 100 долларов и процентная ставка равна 5%, то через год у вас будет 100 * (1 + 5/100)^1 = 105 долларов. Если вы оставите эти деньги на счете еще на один год, то через два года у вас будет 100 * (1 + 5/100)^2 = 110,25 долларов.

Таким образом, экспонента позволяет нам рассчитывать будущие значения на основе процентов и временного периода. Это используется в финансовых расчетах, науке, экономике и других областях, где необходимо прогнозировать изменения на основе процентной ставки.

Использование экспоненты вместе с пониманием процентов позволяет нам лучше понять и предсказывать изменения в различных сферах нашей жизни.

Начальная сумма (S)Процентная ставка (r)Временной период (t)Конечная сумма

100	5%	1 год	105
100	5%	2 года	110,25

Экспонента и логарифмы

Экспонента обозначается символом e и представляет собой особую функцию, которая возведет число в степень. Например, экспонента вида e^x означает, что число e будет возведено в степень x. Экспонента имеет множество свойств, которые делают ее полезной и интересной для исследования.

Логарифмы, с другой стороны, являются обратной операцией экспоненты. Логарифм — это функция, которая позволяет найти степень, в которую нужно возвести основание, чтобы получить заданное число. Например, если мы хотим найти логарифм числа 100 по основанию 10, то мы ищем степень, в которую нужно возвести 10, чтобы получить 100 — это будет 2, так как 10^2 = 100.

Логарифмы имеют множество приложений в математике, физике, экономике и других областях науки. Они позволяют упрощать сложные вычисления, решать уравнения и моделировать различные процессы.

Экспонента и логарифмы являются важными понятиями в математике и имеют широкое применение в различных научных и практических областях. Изучение и понимание этих концепций позволяет решать сложные задачи и строить новые модели.

Применение экспоненты в науке и технике

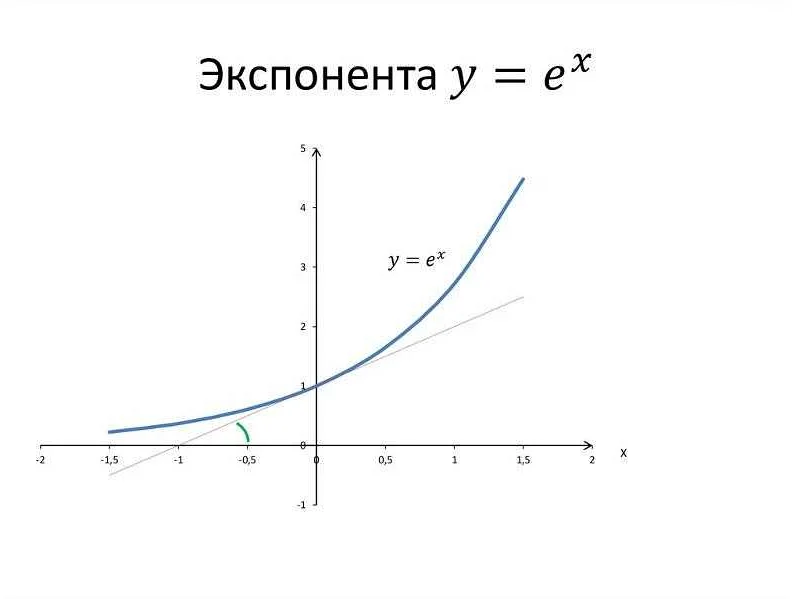
Экспонента, как математическая функция, находит свое применение во многих областях науки и техники. Ее особенности и свойства делают ее полезной и эффективной в различных вычислениях и моделях.

1. Физика

В физике экспонента используется для описания процессов, связанных с ростом и убыванием. Она помогает моделировать радиоактивный распад, заряд и разряд конденсаторов, демонстрирует закон сохранения энергии, а также описывает диффузию веществ и распространение тепла.

2. Электротехника

В электротехнике экспонента применяется при анализе и проектировании электрических цепей. Например, она помогает определить время зарядки и разрядки конденсаторов, характеризуя их поведение во времени.

3. Экономика

В экономике экспонента используется для моделирования экономических процессов. Например, экспоненциальный рост или убывание может быть использован для описания инфляции, роста населения, доходов или стоимости товаров.

4. Биология

В биологии экспонента применяется для моделирования популяций и роста численности организмов. Она помогает описывать изменения численности живых организмов во времени и определять их устойчивость или неустойчивость.

5. Криптография

В криптографии экспонента используется для шифрования и дешифрования данных. Она является основой для различных алгоритмов шифрования, таких как RSA, которые обеспечивают безопасность информации.

Все эти примеры демонстрируют, что экспонента является мощным инструментом для анализа и моделирования различных процессов. Ее свойства, такие как экспоненциальный рост и убывание, позволяют описывать и предсказывать поведение различных систем и явлений в науке и технике.

Вопрос-ответ:

Что такое экспонента?

Экспонента — это математическая функция, которая возведет число в степень. Она имеет вид e^x, где e — основание экспоненты, а x — показатель степени.

Как работает экспонента?

Экспонента работает по принципу возведения числа в степень. Она увеличивает значение числа в геометрической прогрессии. Например, при увеличении значения x, значение экспоненты e^x также увеличивается.

Зачем нужна экспонента в математике?

Экспонента широко используется в математике, физике, химии и других науках. Она помогает моделировать различные процессы, такие как рост популяции, распад вещества, электрические цепи и т.д. Экспонента также важна для решения уравнений и построения графиков.

Какие свойства имеет экспонента?

Экспонента обладает рядом свойств. Например, e^0 = 1, e^1 = e. Также справедливо следующее правило: e^(a+b) = e^a * e^b. Экспонента также обладает производной, равной самой себе: (e^x)’ = e^x.

Как построить график экспоненты?

Для построения графика экспоненты необходимо выбрать набор значений x и вычислить соответствующие значения e^x. Затем эти точки можно отобразить на координатной плоскости и соединить линией, чтобы получить график экспоненты. Обычно график экспоненты имеет форму восходящей кривой, увеличивающейся с ростом x.

Как определить экспоненту в математике?

Экспонента в математике — это функция, которая представляет собой возведение числа в степень. Обычно экспонента обозначается символом «e».

Видео по теме: