Что такое функция в математике 7 класс

Функция в математике 7 класс — это математическое понятие, которое позволяет установить зависимость между двумя переменными в виде правила, при котором каждому значению одной переменной соответствует единственное значение другой переменной. Учащиеся 7 класса изучают основные понятия и свойства функций, а также учатся работать с графиками функций и находить значения функции при заданных значениях переменных.

Функция – одно из ключевых понятий математики, изучаемое в 7 классе. Функция — это закон, сопоставляющий каждому элементу одного множества элемент из другого множества. В математике функции широко используются для описания зависимостей между величинами и решения различных задач.

Основное свойство функции – каждому элементу первого множества соответствует ровно один элемент второго множества. Поэтому функцию можно представить как «машины», которая принимает на вход число и возвращает другое число. Функцию обычно обозначают буквами f, g или h, а входные и выходные значения – x и y.

Например, функция f(x) = 2x + 1 означает, что каждому x соответствует число 2x + 1. Если x = 2, то f(2) = 2 * 2 + 1 = 5.

Функции могут быть представлены в виде таблицы значений, графика или алгоритма. Они могут быть линейными, квадратичными, степенными, тригонометрическими и т.д. У функций есть различные свойства, такие как принадлежность к определенному классу функций, область определения и область значений, монотонность, четность и периодичность.

Изучение функций позволяет ученикам научиться анализировать их свойства, строить графики, решать уравнения и неравенства, а также применять их в решении задач. Понимание функций является важным и необходимым навыком для дальнейшего изучения математики и других наук.

Что такое функция в математике

Функцию можно представить графически с помощью координатной плоскости. График функции – это множество точек, каждая из которых имеет координаты (x, y), где x – значение аргумента, а y – соответствующее значение функции.

Основные свойства функций:

1. Область определения – это множество всех значений аргумента, для которых функция имеет смысл и может быть вычислена.
2. Область значений – это множество всех значений функции, которые могут быть получены при подстановке различных значений аргумента.
3. Значение функции в конкретной точке – это результат вычисления функции при подстановке значения аргумента.
4. Нулевая функция – это функция, у которой все значения равны нулю.
5. Монотонность функции – это свойство функции изменяться только в одном направлении – либо возрастать, либо убывать.
6. Обратная функция – это функция, обратная исходной функции, то есть позволяющая восстановить значение аргумента по известному значению функции.

Знание понятия функции является основой для изучения более сложных математических тем, таких как алгебра, геометрия и анализ. Понимание функций позволяет анализировать зависимости и взаимосвязи между различными величинами и решать разнообразные задачи.

Определение функции

Функция обозначается символом f и записывается в виде f(x), где x — элемент из области определения. То есть, каждому элементу x из области определения соответствует единственный элемент f(x) из области значений.

Область определения функции — это множество всех значений, для которых функция определена. Область значений — это множество всех значений, которые принимает функция.

Например, рассмотрим функцию f(x) = 2x. Областью определения этой функции является множество всех действительных чисел, а областью значений — множество всех удвоенных действительных чисел.

Функции широко применяются в математике, физике, экономике и других науках для описания зависимостей между величинами и решения различных задач.

Основные свойства функций в математике

1. Однозначность:

Каждому элементу из первого множества соответствует только один элемент из второго множества. Это означает, что двум разным элементам из первого множества не могут соответствовать одинаковые элементы из второго множества.

2. Область определения:

Функция имеет определенную область определения, которая состоит из всех возможных значений входных переменных. Функция может быть определена только для тех значений, для которых она имеет смысл.

3. Область значений:

Область значений функции состоит из всех возможных значений выходных переменных. Она определяет множество значений, которые могут быть получены при подстановке различных значений входных переменных.

4. График функции:

График функции — это графическое представление соответствия между входными и выходными переменными. Он представляет собой множество точек на координатной плоскости, где каждая точка имеет координаты (x, y), где x — значение входной переменной, y — значение выходной переменной.

5. Зависимость:

Функция является математическим выражением, которое описывает зависимость между входными и выходными переменными. Это означает, что изменение входной переменной приводит к изменению выходной переменной.

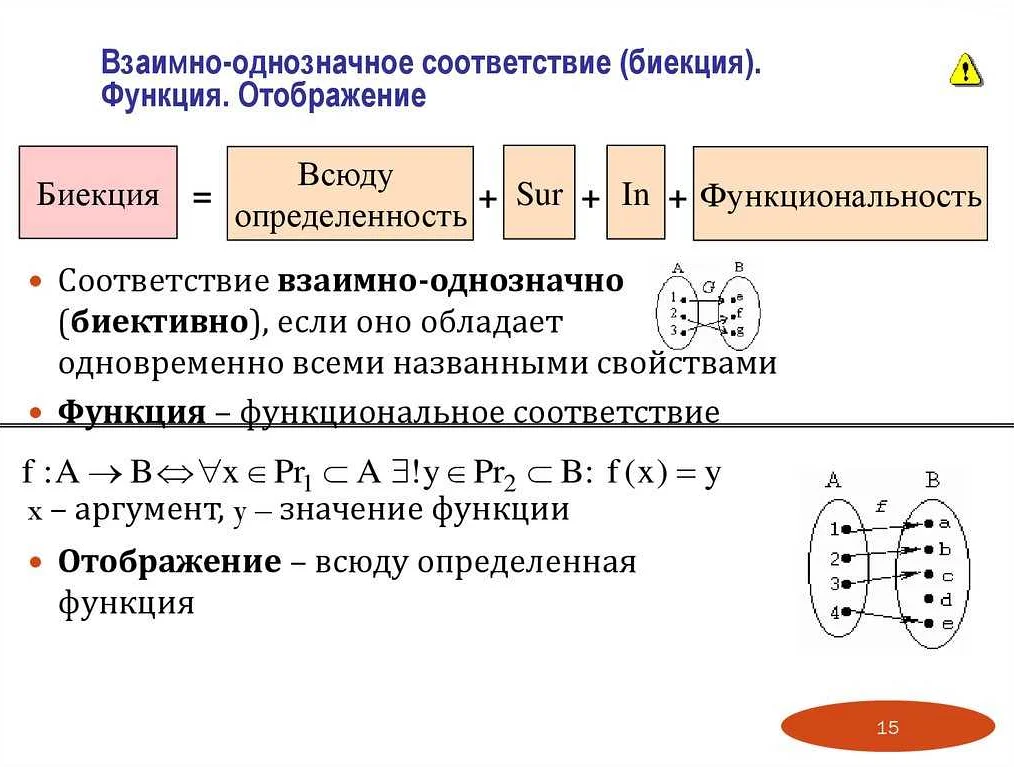
6. Инъективность, сюръективность и биективность:

Функция может быть инъективной (взаимно-однозначной), сюръективной (на) или биективной (взаимно-однозначно на). Инъективная функция означает, что каждому элементу из первого множества соответствует только один элемент из второго множества, сюръективная функция означает, что каждому элементу из второго множества соответствует хотя бы один элемент из первого множества, а биективная функция означает, что каждому элементу из первого множества соответствует ровно один элемент из второго множества, и наоборот.

Эти основные свойства функций играют важную роль в математике и позволяют анализировать и решать различные задачи, связанные с зависимостью между переменными.

Однозначность функции

Функция в математике называется однозначной, если каждому элементу множества X соответствует только один элемент множества Y.

Другими словами, каждому x из множества X соответствует только одно значение y из множества Y.

Если для двух различных элементов x1 и x2 из множества X функция принимает одно и то же значение y из множества Y, то функция не является однозначной.

Однозначность функции очень важна в математике, так как она позволяет установить однозначное соответствие между элементами двух множеств. Это свойство позволяет определить функцию как отображение, которое не может иметь двух различных результатов для одного и того же значения.

Область определения и область значений

Например, для функции f(x) = √x (квадратный корень из x), область определения будет состоять из всех неотрицательных чисел, так как квадратный корень из отрицательного числа не определен.

Область значений функции – это множество всех возможных значений зависимой переменной, которые могут быть получены при заданных значениях независимой переменной. Обычно область значений также задается в виде интервала или объединения нескольких интервалов на числовой оси.

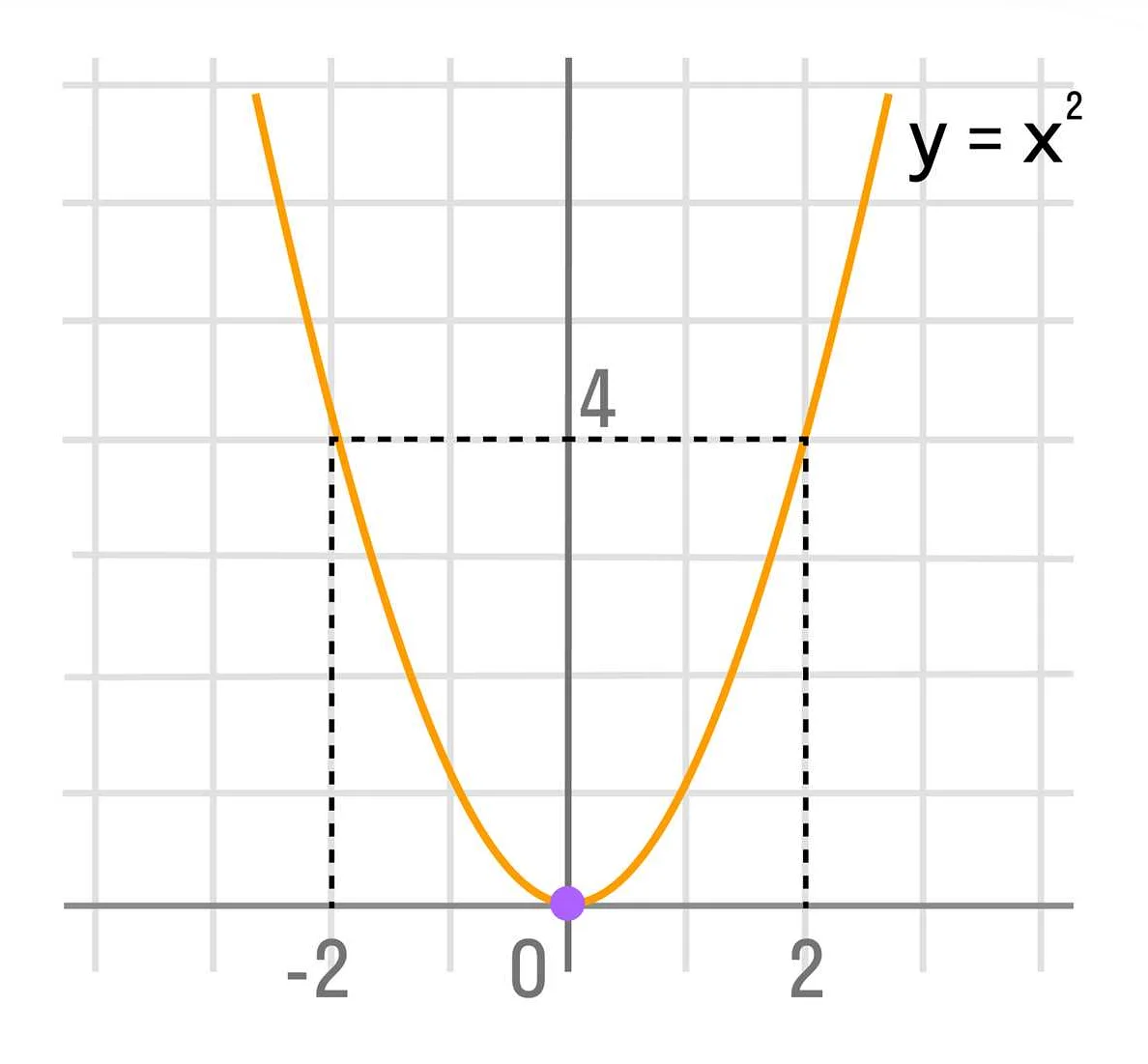
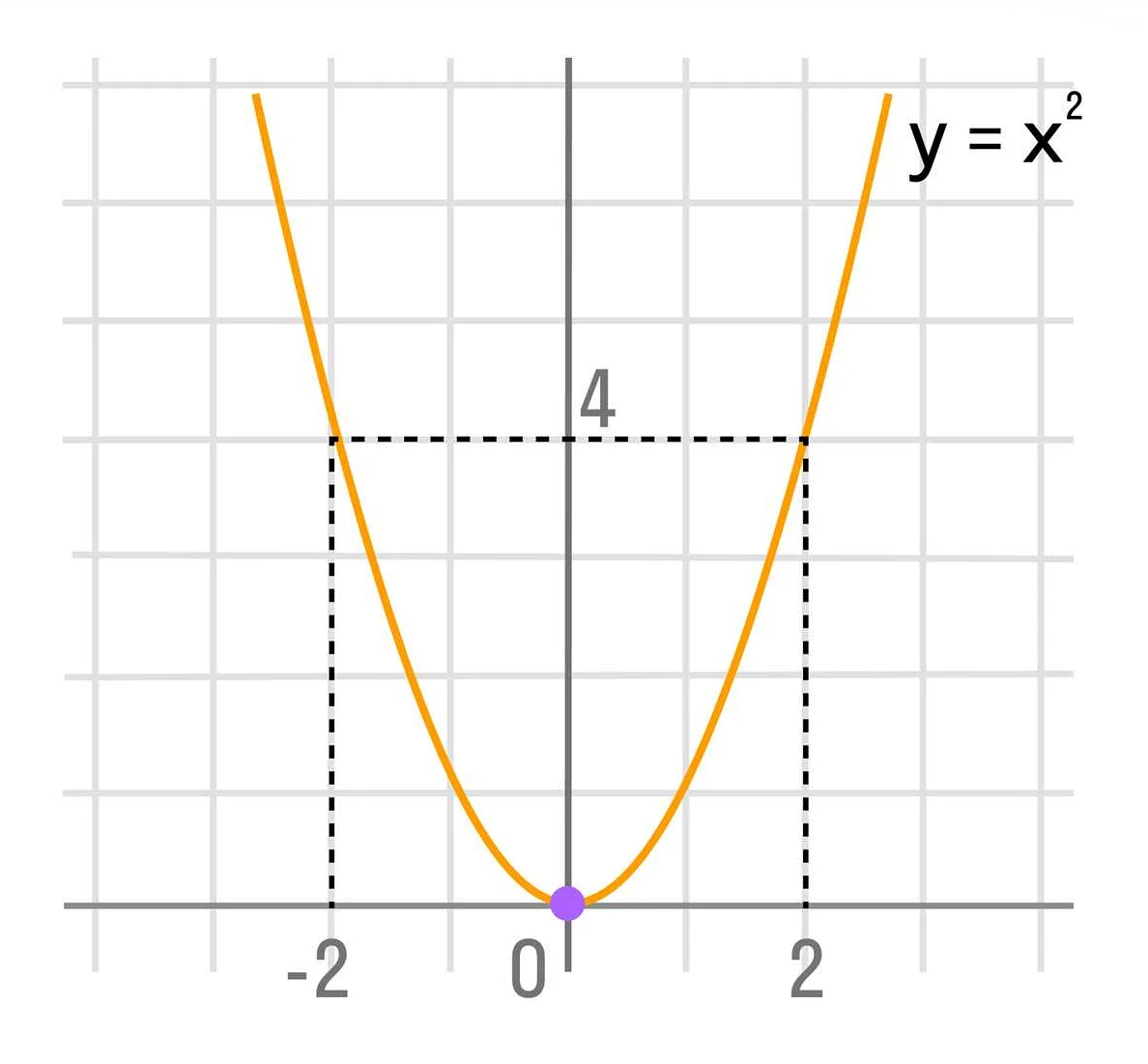
Например, для функции f(x) = x^2 (квадрат числа x), область значений будет состоять из всех неотрицательных чисел, так как квадрат любого числа всегда положителен или равен нулю.

Область определения и область значений являются важными понятиями в математике, которые позволяют определить, какие значения можно использовать при работе с функцией и какие значения она может принимать. Эти понятия помогают анализировать и понимать свойства функций и их поведение.

График функции

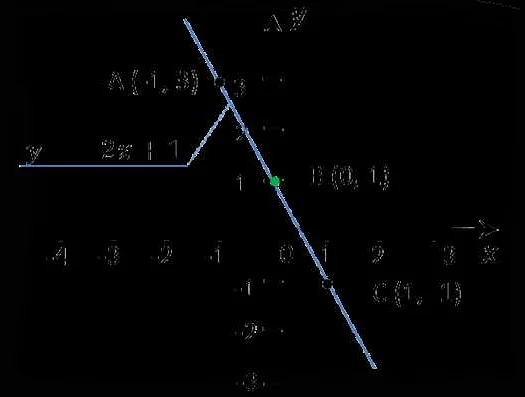
График функции может быть представлен с помощью таблицы значений, где значения аргументов и соответствующие им значения функции записываются в виде пар.

Аргумент (x)Значение функции (y)

-2	4
-1	1
0	0
1	1
2	4

По этим значениям можно построить график функции, откладывая на плоскости точки, соответствующие значениям аргумента и значениям функции.

График функции может быть представлен в виде кривой линии, ломаной или даже отдельных точек на плоскости.

График функции позволяет визуально представить изменение функции в зависимости от значения аргумента. Он помогает анализировать свойства функции, такие как ее поведение на промежутках, точки экстремума, области определения и множество значений.

Примеры функций

В математике существует множество примеров функций, которые могут быть полезными для понимания основных свойств и определений.

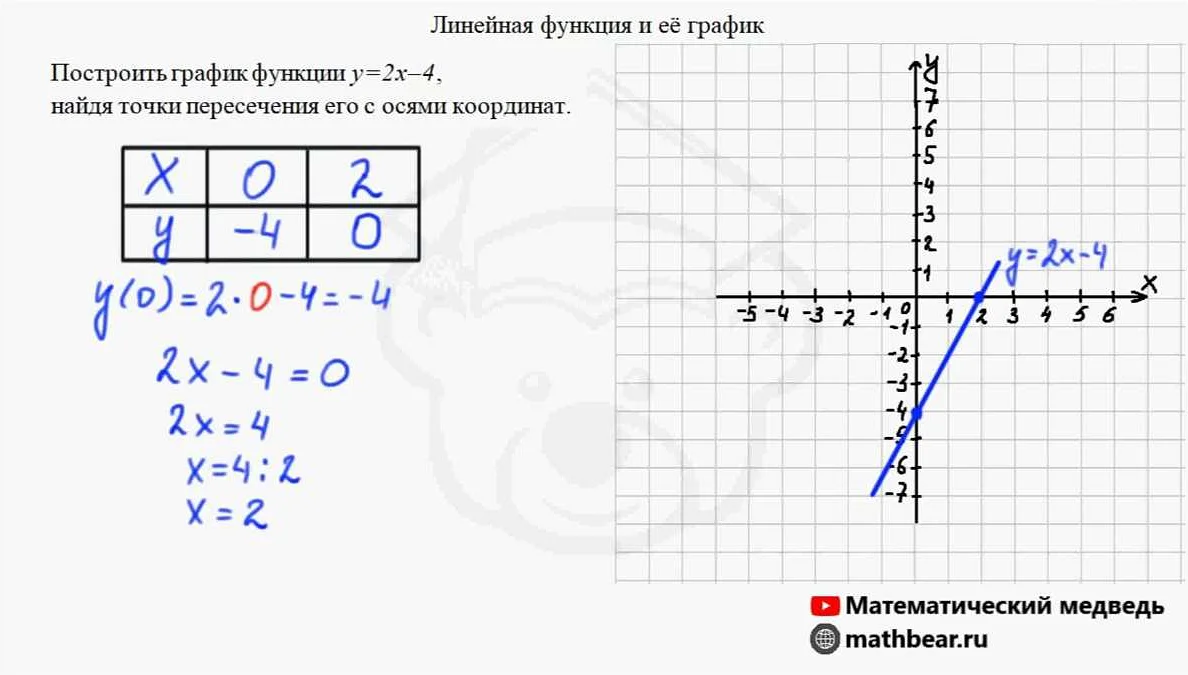
1. Линейная функция: это функция вида f(x) = kx + b, где k и b — константы. Примером линейной функции может быть y = 2x + 1.

2. Квадратичная функция: это функция вида f(x) = ax^2 + bx + c, где a, b и c — константы. Примером квадратичной функции может быть y = x^2 + 3x — 2.

3. Степенная функция: это функция вида f(x) = ax^n, где a и n — константы. Примером степенной функции может быть y = 2x^3.

4. Экспоненциальная функция: это функция вида f(x) = a^x, где a — константа. Примером экспоненциальной функции может быть y = 2^x.

5. Логарифмическая функция: это функция вида f(x) = log_a(x), где a — константа. Примером логарифмической функции может быть y = log_2(x).

Это лишь некоторые примеры функций, которые можно встретить в математике. Каждая из них имеет свои особенности и свойства, которые исследуются в дальнейшем изучении математики.

Свойства функции

Функция в математике обладает рядом особых свойств, которые позволяют ее определить и анализировать. Рассмотрим основные свойства функции:

СвойствоОписание

Определение функции	Функция определяется с помощью правила, по которому каждому элементу из области определения ставится в соответствие ровно один элемент из области значений.
График функции	График функции представляет собой множество точек на плоскости, каждая из которых имеет координаты (x, f(x)), где x — элемент из области определения, а f(x) — соответствующее значение функции.
Область определения	Область определения функции — это множество всех значений, для которых функция определена.
Область значений	Область значений функции — это множество всех значений, которые функция может принимать.
Монотонность функции	Функция называется монотонной, если она либо возрастает на всей своей области определения, либо убывает.
Четность и нечетность функции	Функция называется четной, если f(-x) = f(x) для всех x из области определения, и нечетной, если f(-x) = -f(x) для всех x из области определения.
Предел функции	Предел функции определяет поведение функции вблизи определенной точки. Он позволяет выяснить, куда стремится значение функции, когда аргумент приближается к определенной точке.

Нахождение обратной функции

Обратной функцией к заданной функции f(x) называется такая функция g(x), что при подстановке значения f(x) в функцию g(x) получается исходное значение x.

Для нахождения обратной функции необходимо выполнить следующие шаги:

1. Записать исходную функцию в виде y = f(x).
2. Решить уравнение относительно x, получив x = g(y).
3. Полученное уравнение y = g(x) и будет обратной функцией.

Не всегда у исходной функции существует обратная функция. Для того чтобы функция имела обратную, она должна быть биекцией, то есть каждому значению x должно соответствовать единственное значение y, и наоборот.

Обратная функция позволяет находить значение аргумента, при котором заданная функция принимает определенное значение. Она также используется для решения уравнений и упрощения выражений.

Видео по теме:

Для чего нужна функция в математике?

Функция в математике используется для описания зависимости между двумя величинами. Она позволяет выразить одну величину через другую и понять, как изменяется одна величина при изменении другой.

Как определить функцию?

Функцию можно определить как отображение между двумя множествами, где каждому элементу из первого множества сопоставляется единственный элемент из второго множества. В математической записи это выглядит как f(x) = y, где f — функция, x — аргумент, y — значение функции.

Какие бывают виды функций?

В математике существует множество видов функций. Некоторые из них: линейные функции, квадратные функции, показательные функции, логарифмические функции, тригонометрические функции и др. Каждый вид функции имеет свои особенности и свойства.

Как найти область определения функции?

Область определения функции — это множество всех значений аргумента, при которых функция имеет смысл. Чтобы найти область определения, нужно обратить внимание на ограничения и условия, заданные в задаче или в определении функции. Например, если функция содержит знаменатель, то нужно исключить значения аргумента, при которых знаменатель обращается в ноль.

Какие свойства имеют функции?

Функции в математике обладают различными свойствами. Некоторые из них: свойство четности/нечетности, свойство монотонности, свойство ограниченности, свойство периодичности и др. Знание этих свойств помогает в анализе функций и решении задач.

Что такое функция в математике?

Функция в математике представляет собой особый вид отношения между двумя множествами, где каждому элементу одного множества сопоставляется ровно один элемент другого множества. То есть, функция определяет правило, по которому каждому элементу из одного множества ставится в соответствие элемент из другого множества.