Что такое hod в математике 6 класс

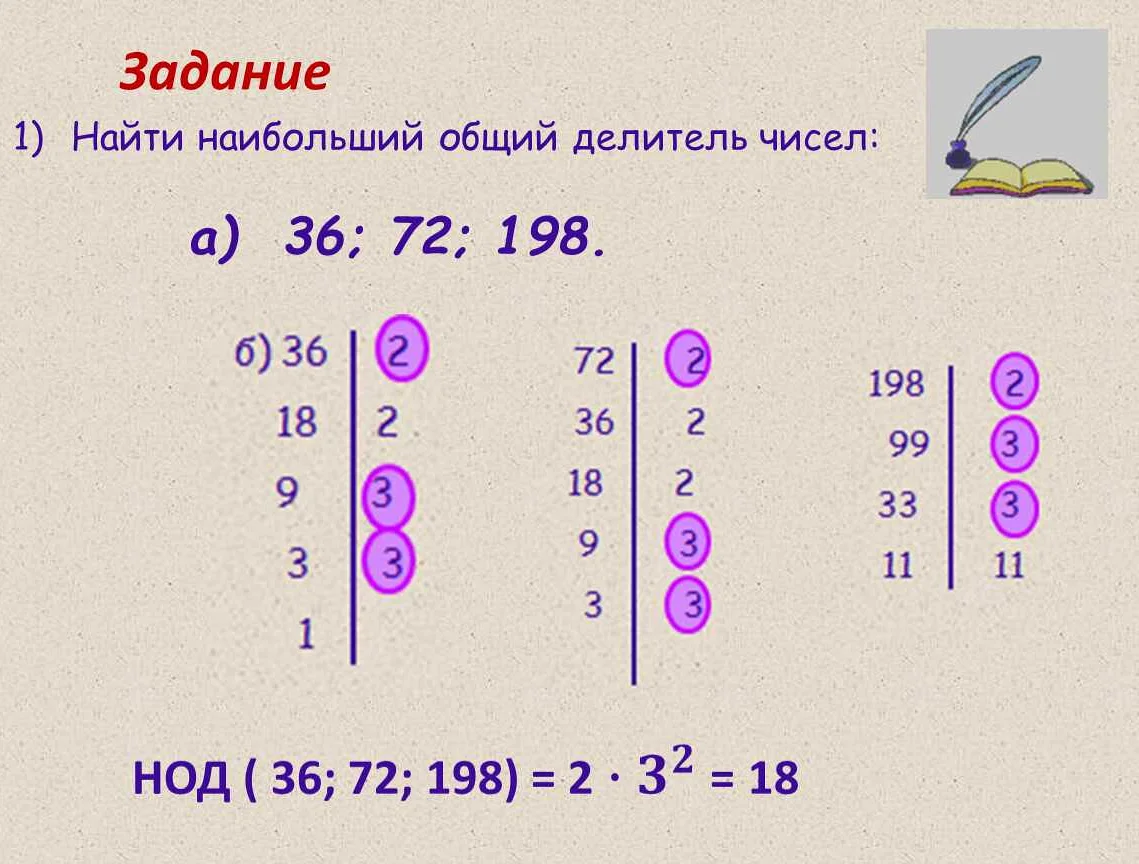
HOD (Наибольший общий делитель) — это математическое понятие, которое используется в 6 классе для нахождения наибольшего общего делителя двух чисел. В данной статье рассматривается, как вычислить hod и приводятся примеры его применения в задачах.

В математике 6 класса hod — это одно из ключевых понятий, которое помогает ученикам понять и применять различные математические операции. HOD — это сокращение от »

Определение хода в математике

Ход может быть сделан на графике, доске или в пространстве. Он может быть выполнен вперед, назад, влево или вправо. В математике ход может быть представлен геометрическими фигурами, такими как точки, отрезки, прямые, углы и многоугольники.

Чтобы понять ход, можно рассмотреть пример: если мы начинаем с точки А и делаем ход влево на одно поле, то мы окажемся в точке В. Если мы продолжим делать ходы на одно поле влево, то мы сможем переместиться до точки С и так далее.

Ходы в математике используются для решения различных задач, включая геометрические и математические головоломки, а также для изучения основных понятий и свойств геометрических фигур.

Значение хода в математическом контексте

В математическом контексте ход может быть представлен разными способами. Один из наиболее распространенных способов — использование координат. Например, если нам нужно описать ход на плоскости, мы можем использовать координаты начальной и конечной точек. Это позволяет нам определить направление и длину хода, а также вычислить его с помощью соответствующих формул.

Примером задачи, которая может быть решена с использованием понятия хода, является нахождение расстояния между двумя точками на плоскости. Для этого мы можем использовать формулу расстояния между двумя точками:

d = √((x2 — x1)² + (y2 — y1)²)

где (x1, y1) и (x2, y2) — координаты начальной и конечной точек соответственно.

Также ход может быть представлен в виде перемещения по числовой оси. В этом случае мы можем использовать положительные и отрицательные числа, чтобы указать направление движения. Например, если мы движемся вправо, мы можем использовать положительные числа, а если движемся влево — отрицательные числа.

Важно понимать, что ход в математике — это абстрактное понятие, которое используется для описания перемещения и решения математических задач. Он широко применяется в различных областях математики, таких как геометрия, алгебра и арифметика.

Примеры использования хода в математике

Ход в математике используется для обозначения перемещения точки или фигуры из одного места в другое. Вот несколько примеров использования хода в различных математических задачах:

1. В задаче на графиках можно использовать ходы для обозначения движения точки по оси координат. Например, если точка начинает с координатами (0, 0) и перемещается вправо на 3 единицы, затем вверх на 2 единицы, ходы можно обозначить как (3, 0) и (0, 2).
2. В задачах на треугольники можно использовать ходы для обозначения перемещения вершин треугольника. Например, если треугольник ABC с вершинами в точках A(0, 0), B(3, 0) и C(0, 2) сдвигается вправо на 2 единицы и вверх на 1 единицу, ходы можно обозначить как (2, 0) и (0, 1).
3. В задачах на преобразования геометрических фигур можно использовать ходы для обозначения поворотов, отражений и сжатий. Например, если прямоугольник ABCD со сторонами AB = 4 и BC = 3 сжимается в 2 раза относительно точки A, ход можно обозначить как (0, 0, 2).

Таким образом, ходы в математике играют важную роль при решении задач, связанных с перемещением точек и фигур, а также при преобразованиях геометрических объектов.

Практическое применение хода в решении задач

Практическое применение хода может быть разнообразным и зависит от конкретной задачи. Вот несколько примеров, где использование хода помогает в решении задач:

1. Упрощение выражений. Ходы позволяют сокращать или преобразовывать сложные математические выражения, делая их более понятными и удобными для работы. Например, можно использовать ходы для сокращения дробей или объединения подобных членов в алгебраических выражениях.
2. Решение уравнений. Ходы помогают преобразовывать уравнения, чтобы найти значение неизвестной переменной. Например, можно применить ходы для выделения неизвестной в одну сторону уравнения или для приведения уравнения к каноническому виду.
3. Нахождение общих закономерностей. Ходы позволяют проводить различные преобразования над числами или геометрическими фигурами, чтобы найти общие закономерности или связи между ними. Например, можно использовать ходы для нахождения формул для площади или периметра различных фигур.
4. Доказательство теорем. Ходы также могут использоваться для доказательства математических теорем. Они позволяют преобразовывать высказывания и использовать логические законы, чтобы получить нужное утверждение. Например, можно применить ходы для доказательства теоремы о сумме углов треугольника или теоремы Пифагора.

Все эти примеры показывают, как ходы могут быть полезны в решении различных математических задач. Они помогают упростить вычисления, найти решение уравнений, найти общие закономерности и доказать теоремы. Понимание и умение применять ходы является важной частью математической грамотности и помогает развивать логическое мышление и аналитические навыки.

Значимость хода в понимании математических концепций

С помощью ходов мы можем применять математические правила и операции для преобразования и упрощения выражений, нахождения решений уравнений или доказательства математических теорем.

Значимость хода заключается в том, что он позволяет нам преобразовывать математические выражения и решать задачи шаг за шагом, постепенно приближаясь к искомому результату. Каждый ход имеет свою цель и логическое обоснование, которое помогает понять и объяснить математическую идею или принцип.

Понимание ходов и их значимости помогает развить у учеников навыки логического мышления, абстрактного и аналитического мышления, а также умение применять математические знания на практике.

Примеры ходов в математике включают в себя:

• Подстановка числовых значений вместо переменных;
• Применение арифметических операций (сложение, вычитание, умножение, деление);
• Факторизация и раскрытие скобок;
• Применение свойств равенства и неравенства;
• Применение правил алгебры и геометрии;
• Использование таблиц и графиков для анализа данных.

Осознанное использование ходов в математике помогает ученикам развить способность анализировать, решать проблемы и принимать обоснованные математические решения.

Как использовать ход для решения уравнений

Ход используется для решения уравнений, позволяя найти значение неизвестной переменной. Для этого нужно выполнить несколько шагов:

1. Сначала выделим все члены уравнения с неизвестной переменной на одну сторону, а все остальные члены на другую сторону. Например, если уравнение имеет вид 2x + 5 = 11, мы выделим 2x на одну сторону, а 5 и 11 на другую.
2. Далее выполним необходимые арифметические операции для решения уравнения. В данном случае, чтобы найти значение переменной x, нужно из 11 вычесть 5, получив 6.
3. Теперь полученное значение переменной x является решением уравнения. В данном случае, x = 6.

Таким образом, мы использовали ход для решения уравнения и нашли значение неизвестной переменной.

Приведем еще один пример использования хода для решения уравнения:

ХодыУравнениеРешение

Выделить все члены с неизвестной переменной	3y — 7 = 5	3y = 12
Выполнить необходимые арифметические операции		y = 4

В данном примере мы использовали ход и нашли значение переменной y, равное 4.

Вопрос-ответ:

Что означает термин «hod» в математике?

В математике «hod» означает выражение «хорошо описанная последовательность», которая часто используется в задачах и упражнениях.

В 6 классе какие примеры можно привести для объяснения понятия «hod»?

Например, пусть задана последовательность чисел 2, 4, 6, 8. Это hod, так как она хорошо описывает возрастающую арифметическую последовательность с шагом 2.

Можно ли сказать, что hod и последовательность — это одно и то же?

Нет, hod — это особый тип последовательности, который хорошо описывает определенную закономерность чисел или объектов.

Каким образом можно использовать понятие hod в математических задачах?

Понятие hod позволяет описать и анализировать различные закономерности и зависимости между числами или объектами, что помогает в решении задач и упражнений.

Какими свойствами должна обладать последовательность, чтобы можно было сказать, что она — hod?

Для того, чтобы последовательность могла считаться hod, она должна быть хорошо определена и иметь явные закономерности или правила, по которым можно продолжить последовательность.

Что такое hod в математике?

HOD (Наибольший общий делитель) — это самое большое число, на которое делятся два или более числа без остатка.

Как можно определить HOD?

Для определения HOD двух чисел можно использовать различные методы, включая метод разложения на простые множители, метод Евклида и метод таблицы делителей.

Позитивные эффекты использования хода в преподавании математики

Использование хода в преподавании математики имеет множество положительных эффектов, которые могут улучшить процесс обучения и понимание материала учащимися.

• Активное участие: Включение хода в урок позволяет ученикам активно участвовать в процессе обучения. Они не только слушают лекцию, но и принимают активное участие в решении задач и поиске решений.
• Практическое применение: Ход позволяет ученикам применить полученные знания на практике. Решая задачи и применяя математические концепции на практике, ученики лучше понимают и запоминают материал.
• Развитие логического мышления: Ход способствует развитию логического мышления учеников. Они учатся анализировать, сопоставлять и применять математические правила и концепции в различных ситуациях.
• Сотрудничество и коммуникация: Ход может включать в себя работу в группах или партнерскую работу, что способствует развитию навыков сотрудничества и коммуникации.
• Мотивация: Использование хода может стимулировать интерес учеников к математике и повысить их мотивацию к учению. Более интерактивный и увлекательный урок помогает ученикам поддерживать интерес и вовлеченность в процессе обучения.

Использование хода в преподавании математики является эффективным методом, который помогает студентам лучше понять и применять математические концепции. Он также развивает навыки сотрудничества, коммуникации и логического мышления. Положительные эффекты использования хода делают процесс обучения интереснее и эффективнее для учащихся.

Видео по теме: