Нод что это в математике как найти

Нод (наибольший общий делитель) — это число, которое одновременно является делителем для двух или более чисел. Нахождение НОДа требует использования алгоритма, например, алгоритма Евклида. Узнайте, как найти НОД чисел и решать математические задачи, связанные с этим понятием.

НОД (наибольший общий делитель) – это одно из важных понятий в математике, которое используется для определения общих делителей двух или более чисел. НОД является наибольшим числом, которое делит без остатка все числа, для которых он определен. Он широко применяется в различных областях математики, таких как теория чисел, алгебра, геометрия и др.

Существует несколько простых способов нахождения НОД. Один из них – это метод деления с остатком, известный также как алгоритм Евклида. Суть этого метода заключается в последовательном делении одного числа на другое с вычислением остатка до тех пор, пока остаток не станет равным нулю. После этого НОД будет равен последнему ненулевому остатку.

Пример: Найти НОД для чисел 24 и 36.

Шаг 1: 36 ÷ 24 = 1, остаток 12

Шаг 2: 24 ÷ 12 = 2, остаток 0

НОД(24, 36) = 12

Еще одним способом нахождения НОД является факторизация чисел. Для этого необходимо разложить каждое число на простые множители и найти их общие множители. НОД будет равен произведению всех общих множителей с наименьшими степенями.

Найденный НОД позволяет решать множество задач, связанных с дробями, уравнениями, алгоритмами и другими математическими операциями. Понимание и умение находить НОД полезны не только в математике, но и в повседневной жизни, например для упрощения дробей или определения общего масштаба в задачах геометрии.

Что такое нод в математике

Понимание НОДа имеет важное значение в различных областях математики, включая алгебру, арифметику, теорию чисел и др. Например, НОД используется для упрощения дробей, решения уравнений и нахождения общих множителей.

Найти НОД можно с помощью различных методов, включая метод деления, метод эратосфена и алгоритм Евклида.

Метод деления используется для нахождения НОД двух чисел путем последовательного деления одного числа на другое до тех пор, пока не будет получен остаток ноль. Последний ненулевой остаток будет являться НОДом.

Метод эратосфена используется для нахождения НОД нескольких чисел. Он основан на поиске простых чисел, которые делят все числа из заданного набора. Процесс повторяется до тех пор, пока не будет найдено общее простое число, которое делит все числа, и оно станет НОДом.

Алгоритм Евклида является наиболее распространенным способом нахождения НОД двух чисел. Этот метод основан на последовательном делении одного числа на другое с вычитанием остатка. Процесс повторяется до тех пор, пока не будет получен нулевой остаток, и последнее ненулевое число будет являться НОДом.

НОД имеет множество приложений и используется в различных областях математики и науки. Понимание этой концепции поможет в решении различных математических задач и облегчит работу с числами.

Значение и определение

НОД может быть найден с помощью нескольких простых способов. Один из них — это метод деления. В этом методе два числа делятся друг на друга до тех пор, пока не будет получен ноль в остатке. НОД будет равен последнему ненулевому остатку.

Еще один способ нахождения НОД — это разложение чисел на простые множители. Каждое число разлагается на простые множители, затем находится их общий набор и произведение этих простых множителей будет НОД.

Знание НОД имеет практическое значение в различных областях, таких как криптография, алгоритмы и решение уравнений.

Примеры и применение

1. Дроби: НОД используется для сокращения дробей до наименьших возможных значений. Например, если имеется дробь 8/12, то НОД чисел 8 и 12 равен 4, и дробь можно сократить до 2/3.
2. Рациональные числа: НОД используется для определения эквивалентности рациональных чисел. Два рациональных числа считаются эквивалентными, если они могут быть представлены в виде a/b и c/d, где a, b, c и d являются целыми числами, а НОД(b, d) = 1.
3. Алгоритм Евклида: Это один из наиболее распространенных способов нахождения НОДа двух чисел. Алгоритм Евклида основан на простом принципе: НОД(a, b) равен НОД(b, a mod b), где a mod b — это остаток от деления a на b. Это простой и эффективный способ нахождения НОДа.
4. Шифрование: НОД используется в некоторых алгоритмах шифрования. Например, в RSA шифровании НОД используется для генерации публичного и приватного ключей.

Это лишь несколько примеров применения НОДа в математике и криптографии. НОД играет важную роль в многих других областях, и его понимание позволяет решать различные задачи и проблемы.

Как найти нод

Существует несколько способов определения НОДа:

1. Метод простых делителей:

Для нахождения НОДа двух чисел можно разложить их на простые множители и найти наибольший общий простой делитель. Например, для чисел 12 и 15 можно разложить их на простые множители: 12 = 2 * 2 * 3, 15 = 3 * 5. Наибольший общий простой делитель равен 3.

2. Метод деления:

Для нахождения НОДа двух чисел можно использовать метод деления. Для этого нужно разделить большее число на меньшее и найти остаток от деления. Затем остаток следует поделить на предыдущий остаток до тех пор, пока остаток не станет равным нулю. Наибольший общий делитель равен последнему ненулевому остатку. Например, для чисел 24 и 18:

24 ÷ 18 = 1 (остаток 6)

18 ÷ 6 = 3 (остаток 0)

Наибольший общий делитель равен 6.

3. Метод Эвклида:

Для нахождения НОДа двух чисел можно использовать алгоритм Эвклида. Алгоритм заключается в последовательном нахождении остатков от деления двух чисел и замене чисел на соответствующие остатки до тех пор, пока не будет получен нулевой остаток. Наибольший общий делитель равен последнему ненулевому остатку. Например, для чисел 24 и 18:

24 ÷ 18 = 1 (остаток 6)

18 ÷ 6 = 3 (остаток 0)

Наибольший общий делитель равен 6.

Выбор метода для нахождения НОДа зависит от конкретной задачи и доступных инструментов.

Метод Эвклида для двух чисел

Для примера, пусть нам нужно найти НОД чисел 12 и 18:

1. Большее число 18 вычитаем из меньшего числа 12. Получаем 6.
2. Теперь большее число 12 вычитаем из полученного числа 6. Получаем 6.
3. Так как получили два равных числа (6), то 6 является НОД чисел 12 и 18.

Метод Эвклида можно использовать для нахождения НОД любых двух чисел. Для этого нужно последовательно вычитать меньшее число из большего, пока не получится два равных числа. Этот алгоритм эффективен и прост в реализации.

Расширенный алгоритм Эвклида

a * x + b * y = НОД(a, b),

где a и b – заданные числа.

Расширенный алгоритм Эвклида применяется, например, в криптографии для решения линейных диофантовых уравнений и нахождения обратного элемента в кольце по модулю.

Алгоритм работает следующим образом:

1. Пусть a и b – заданные числа, причем a >= b. Если b = 0, то НОД(a, b) = a и x = 1, y = 0.
2. Если b ≠ 0, применим алгоритм Эвклида для чисел b и a mod b, где a mod b – остаток от деления a на b.
3. По полученным значениям НОД(b, a mod b), x’ и y’, можно найти НОД(a, b) и представление a и b через x и y следующим образом:

• НОД(a, b) = НОД(b, a mod b)
• x = y’
• y = x’ — (a div b) * y’

Таким образом, расширенный алгоритм Эвклида позволяет находить НОД и линейное представление двух чисел. Это полезный инструмент для решения различных задач, связанных с множеством целых чисел.

Метод простых делителей

Для применения метода простых делителей необходимо выполнить следующие шаги:

1. Найти наименьшее простое число, на которое одновременно делится и первое, и второе число.
2. Умножить найденное простое число на результат деления первого числа на него и на результат деления второго числа на него.
3. Повторить шаги 1 и 2 до тех пор, пока оба числа не станут равными единице.

Таким образом, последовательное нахождение простых делителей и их умножение позволяет найти наибольший общий делитель двух чисел.

Метод простых делителей является простым и эффективным способом определения НОД. Однако, для больших чисел может потребоваться значительное количество шагов и времени для нахождения результата.

Вопрос-ответ:

Что такое наибольший общий делитель (НОД)?

Наибольший общий делитель (НОД) двух или более целых чисел — это наибольшее целое число, которое делит все заданные числа без остатка.

Зачем нужно находить наибольший общий делитель (НОД)?

Нахождение НОД может быть полезным во многих математических задачах и алгоритмах, таких как упрощение дробей, нахождение общего знаменателя, решение линейных диофантовых уравнений и других.

Как найти НОД двух чисел?

Существует несколько способов нахождения НОД двух чисел. Один из самых простых способов — это использовать алгоритм Евклида. Для этого нужно разделить большее число на меньшее, затем найти остаток от деления и повторять этот процесс до тех пор, пока не получится остаток равный 0. Последнее ненулевое число будет НОД.

Можно ли использовать алгоритм Евклида для нахождения НОД большего количества чисел?

Да, алгоритм Евклида можно использовать для нахождения НОД большего количества чисел. Для этого нужно последовательно находить НОД между каждой парой чисел, затем использовать полученные НОД для нахождения НОД с оставшимися числами. Процесс повторяется до тех пор, пока не останется одно число, которое будет НОД исходных чисел.

Есть ли еще способы нахождения НОД?

Да, существуют и другие способы нахождения НОД. Например, можно разложить каждое число на простые множители и найти их общие множители. НОД будет произведением этих общих множителей. Также существует метод Бине, основанный на разложении чисел в виде суммы степеней двойки.

Что такое нод в математике?

НОД (наибольший общий делитель) — это наибольшее число, которое одновременно делится на все заданные числа.

Метод сравнения остатков

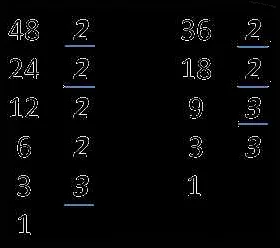
Для применения этого метода нужно выбрать два числа, для которых необходимо найти НОД, и разделить их на одно и то же число, получив остатки. Затем сравнить полученные остатки и повторить процесс с полученными остатками до тех пор, пока не будет получен остаток, равный нулю. Этот остаток будет являться НОД выбранных чисел.

Процесс выглядит следующим образом:

1. Выберите два числа, для которых необходимо найти НОД.
2. Разделите эти числа на одно и то же число и запишите полученные остатки.
3. Сравните полученные остатки.
4. Если остатки равны, то это и есть НОД выбранных чисел.
5. Если остатки не равны, то повторите процесс с полученными остатками.
6. Продолжайте повторять процесс до тех пор, пока не будет получен остаток, равный нулю.
7. Полученный остаток, равный нулю, будет являться НОД выбранных чисел.

Таким образом, метод сравнения остатков позволяет легко определить наибольший общий делитель двух чисел, не требуя сложных математических вычислений.

Видео по теме: