Чем отличается нок от нод в математике
Содержимое
Нок (наименьшее общее кратное) и нод (наибольший общий делитель) являются важными понятиями в математике. Нок — это наименьшее число, которое делится на все заданные числа, а нод — это наибольшее число, на которое делятся все заданные числа. Узнайте, как эти два понятия отличаются друг от друга и как они используются в решении математических проблем.
Нок и нод — это два важных понятия в математике, которые применяются в различных областях, таких как арифметика, алгебра и теория чисел. Нок и нод обычно используются для нахождения наименьшего общего кратного и наибольшего общего делителя двух или более чисел.
Нок, или наименьшее общее кратное, двух или более чисел — это наименьшее число, которое делится на все эти числа без остатка. Нок может быть полезен, например, при решении задач на временах и расстояниях. Например, если нужно найти время, через которое два автомобиля встретятся, зная их скорости и начальные расстояния, можно воспользоваться понятием нок.
Нод, или наибольший общий делитель, двух или более чисел — это наибольшее число, на которое делятся все эти числа без остатка. Нод может быть полезным, например, при сокращении дробей до простейших видов или при нахождении общего множителя в алгебраических выражениях. Например, если нужно сложить или вычесть две дроби с разными знаменателями, можно воспользоваться понятием нод для приведения дробей к общему знаменателю.
Важно отметить, что нок и нод — это взаимосвязанные понятия: значение нод двух чисел равно произведению этих чисел, деленному на их нок.
Определение нок и нод в математике
Наименьшее общее кратное (нок) двух чисел — это наименьшее число, которое делится на оба исходных числа без остатка. Например, для чисел 6 и 9, нок будет равен 18. То есть, 18 делится и на 6, и на 9, без остатка.
Наибольший общий делитель (нод) двух чисел — это наибольшее число, которое делится на оба исходных числа без остатка. Например, для чисел 8 и 12, нод будет равен 4. То есть, 4 делится и на 8, и на 12, без остатка.
Нок и нод являются важными понятиями в математике и находят широкое применение в различных областях, таких как алгебра, арифметика, теория чисел и др.
Что такое нок
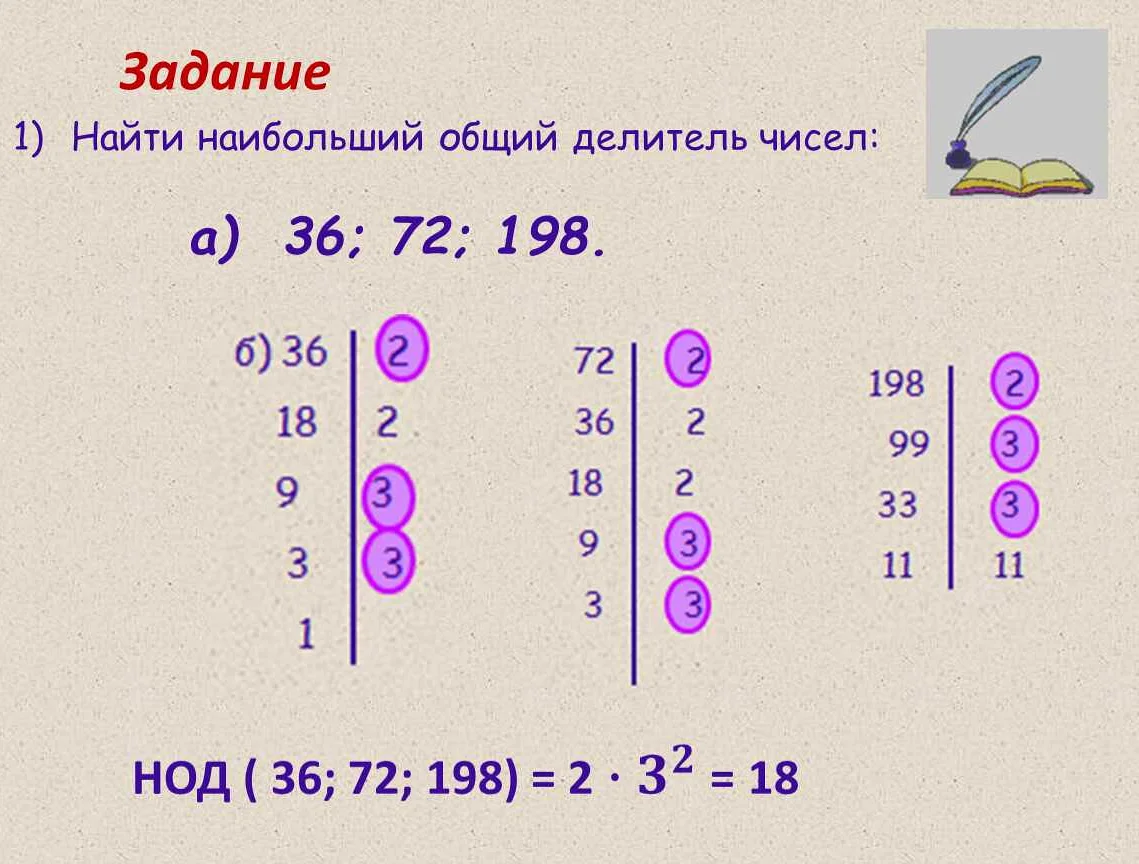
Для двух чисел нок можно найти с помощью разложения их на простые множители и выбора наибольших степеней каждого простого множителя. Например, для чисел 12 и 18, их разложение на простые множители будет: 12 = 2^2 * 3, 18 = 2 * 3^2. Наименьшее общее кратное будет равно 2^2 * 3^2 = 36.
Нок используется, например, для решения задач с периодическими явлениями, когда нужно найти общий период или цикл повторения. Он также полезен при работе с дробями, когда нужно привести их к общему знаменателю.
Нок отличается от нод (наибольший общий делитель), который является наибольшим положительным числом, на которое делятся все заданные числа без остатка.
Что такое нод
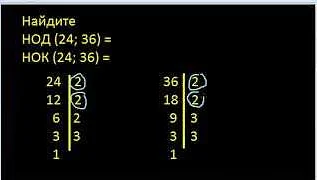
Наибольший общий делитель может быть вычислен с помощью различных алгоритмов, таких как алгоритм Евклида или расширенный алгоритм Евклида. Алгоритм Евклида основан на простой итеративной процедуре нахождения наибольшего общего делителя двух чисел путем последовательного деления одного числа на другое и нахождения остатка.
Нод может быть полезен во многих областях математики и науки, таких как криптография, теория чисел, алгебра и др. Он используется для решения различных задач, например, для сокращения дробей, нахождения общего знаменателя, нахождения периодичности в последовательностях чисел и т.д.
Для вычисления нод можно использовать как простые методы, так и более сложные алгоритмы в зависимости от требуемой точности и эффективности вычислений.
Различия между нок и нод
Нок двух чисел представляет собой наименьшее число, которое делится без остатка на оба этих числа. Например, нок чисел 4 и 6 равен 12, так как 12 делится на 4 и 6 без остатка. Нок часто используется при работе с дробями или при решении задач, связанных с периодичностью.
Нод двух чисел представляет собой наибольшее число, на которое делятся оба этих числа без остатка. Например, нод чисел 12 и 18 равен 6, так как 6 является наибольшим общим делителем для 12 и 18. Нод широко используется при сокращении дробей или при решении задач, связанных с разложением чисел на простые множители.
Таким образом, основное отличие между нок и нод заключается в том, что нок находит наименьшее общее кратное двух чисел, а нод находит наибольший общий делитель этих чисел. Эти понятия имеют разные применения и используются в различных областях математики и ее приложений.
Делимость и нок
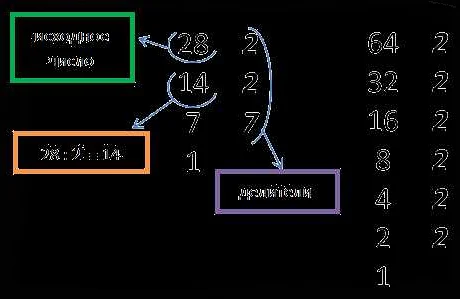
Наименьшим общим кратным (НОК) двух или более чисел называется наименьшее число, которое делится нацело на все эти числа. НОК может быть найден с помощью разложения чисел на простые множители и выбора наименьших степеней каждого простого числа.
НОК является одним из ключевых понятий в теории чисел и широко применяется в различных областях математики, физики и информатики. Он используется для решения задач, связанных с периодичностью, последовательностями и циклическими структурами.
Делимость и НОК являются важными понятиями в математике, которые позволяют решать различные задачи и упрощать вычисления. Понимание этих понятий позволяет более глубоко и точно анализировать различные математические явления и свойства чисел.
Делимость и нод

Наибольший общий делитель (НОД) – это наибольшее число, которое одновременно является делителем для двух или более чисел. Например, для чисел 12 и 18 наибольший общий делитель равен 6.
Для нахождения НОДа существует несколько методов, включая метод деления, метод Евклида и метод факторизации. Наиболее распространенным и эффективным методом является метод Евклида, который основан на последовательных делениях.
Метод Евклида заключается в следующем:
- Делаем деление одного числа на другое и записываем остаток.
- Делаем деление полученного остатка на предыдущий остаток и записываем новый остаток.
- Продолжаем делить до тех пор, пока не получим нулевой остаток.
- Наибольший общий делитель равен последнему ненулевому остатку.
Например, для нахождения НОДа чисел 12 и 18 по методу Евклида:
- Делим 18 на 12 и получаем остаток 6.
- Делим 12 на 6 и получаем остаток 0.
Таким образом, НОД чисел 12 и 18 равен 6.
Наибольший общий делитель используется во многих математических задачах, включая сокращение дробей, решение линейных диофантовых уравнений и поиск наименьшего общего кратного.
Важно отметить, что НОД всегда является положительным числом.
Примеры использования нок и нод
Пример использования нок:
Если у нас есть две фабрики, которые производят одинаковые товары и работают с разной скоростью, нок может помочь нам определить момент, когда эти фабрики будут производить одинаковое количество товаров. Например, если одна фабрика производит товары каждые 30 минут, а другая — каждые 45 минут, нам нужно найти наименьшее число минут, чтобы обе фабрики произвели одинаковое количество товаров. В этом случае нок будет равен 90 минутам.
Пример использования нод:
Нод также может быть полезен для нахождения простых долей и общих множителей. Например, если у нас есть две дроби: 2/3 и 4/6, мы можем использовать нод для упрощения этих дробей. Нод числителей (2 и 4) равен 2, а нод знаменателей (3 и 6) равен 3. Деление числителей и знаменателей на их соответствующий нод даст нам упрощенные дроби: 2/3 и 2/3. Таким образом, мы можем использовать нод для нахождения наиболее упрощенной формы дробей.
Вывод:
Нок и нод являются мощными математическими инструментами, которые могут быть использованы в различных ситуациях. Они помогают нам находить общие решения и упрощать сложные задачи. Понимание этих концепций может полезно не только в математике, но и в реальной жизни.
Примеры использования нок
НОК (наименьшее общее кратное) используется в различных областях математики и ее приложениях. Вот некоторые примеры:
- В школьных задачах: НОК используется для нахождения общего знаменателя и наименьшего общего кратного в дробях. Например, при сложении или вычитании дробей необходимо найти их общий знаменатель с помощью НОК.
- В расписании и графиках: НОК используется для нахождения общего интервала времени или цикла в расписании или графике. Например, при планировании работы различных процессов или при определении периода повторения событий.
- В теории чисел: НОК используется для решения различных задач, связанных с делением чисел и нахождением периодических последовательностей. Например, для нахождения периода повторения десятичной дроби или для определения общего делителя двух чисел.
- В программировании: НОК используется для оптимизации алгоритмов и обработки данных. Например, для определения времени выполнения цикла или для синхронизации процессов и потоков.
Это лишь некоторые примеры использования НОК. В целом, НОК является важным понятием в математике и находит применение во многих областях.
Вопрос-ответ:
Что такое НОК и НОД?
НОК (наименьшее общее кратное) и НОД (наибольший общий делитель) — это понятия в математике, которые используются для работы с целыми числами. НОК двух или более чисел — это наименьшее число, которое делится на все эти числа без остатка. НОД двух или более чисел — это наибольшее число, на которое все эти числа делятся без остатка.
Как найти НОК двух чисел?
Для нахождения НОК двух чисел нужно разложить каждое число на простые множители и взять все множители вместе с максимальными степенями, в которых они встречаются. Затем перемножить эти множители. Полученное число будет являться НОК исходных чисел.
Как найти НОД двух чисел?
Для нахождения НОД двух чисел нужно разложить каждое число на простые множители и взять все общие множители с минимальными степенями, в которых они встречаются. Затем перемножить эти множители. Полученное число будет являться НОД исходных чисел.
В чем отличие НОК от НОД?
Главное отличие между НОК и НОД заключается в том, что НОК — это наименьшее число, которое делится на все заданные числа без остатка, а НОД — это наибольшее число, на которое делятся все заданные числа без остатка. НОК используется, когда требуется найти наименьшую общую кратную, а НОД — когда требуется найти наибольший общий делитель.
Зачем нужны НОК и НОД в математике?
НОК и НОД широко используются в различных областях математики. Например, они нужны при решении уравнений, при сокращении дробей, при нахождении простых чисел и многих других задачах. Также НОК и НОД имеют практическое применение в реальной жизни, например, при расчете времени совместной работы двух или более устройств.
Что такое НОК и НОД?
НОК (наименьшее общее кратное) и НОД (наибольший общий делитель) — это два понятия, которые часто используются в математике для работы с числами. НОК двух чисел — это наименьшее число, которое делится на оба заданных числа без остатка. НОД двух чисел — это наибольшее число, которое делит оба заданных числа без остатка.
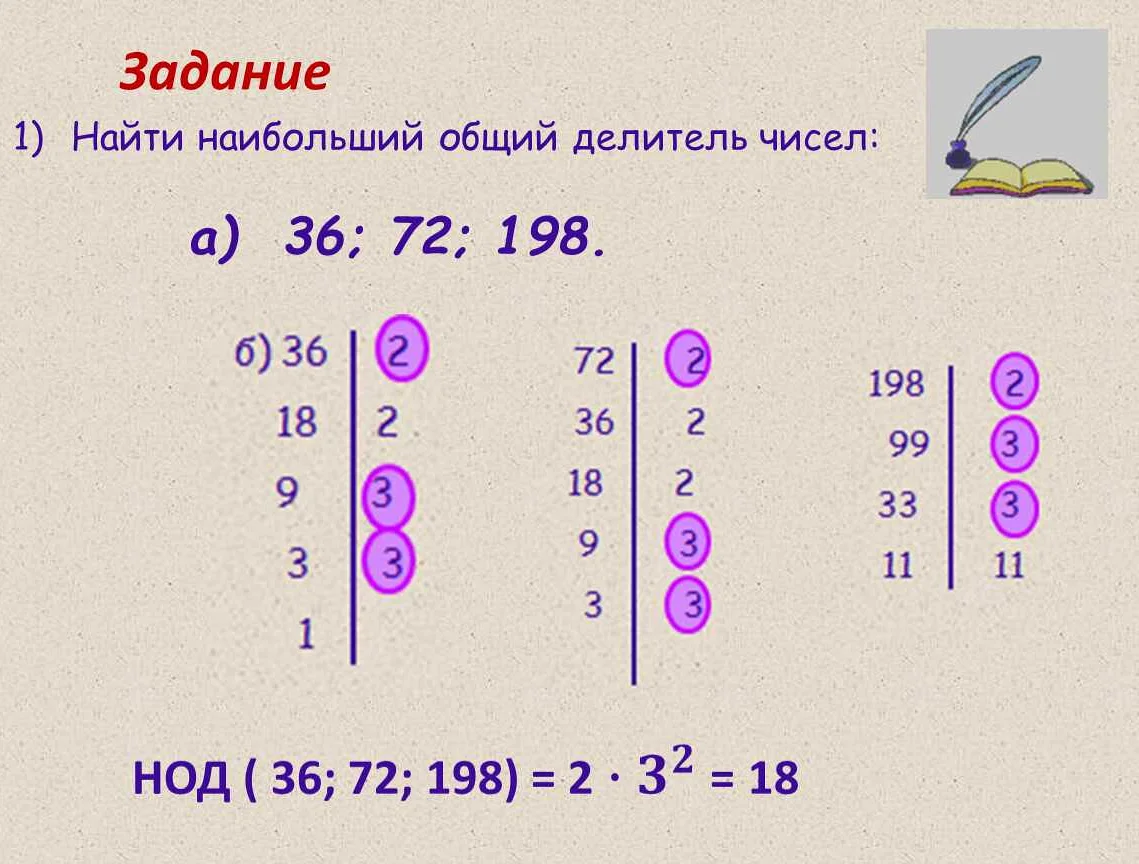



Спасибо за интересную статью! Очень понравилось узнать о понятиях «нок» и «нод» в математике. Я всегда думала, что эти термины используются только в программировании, но оказывается, они имеют глубокий математический смысл. Нок, или наименьшее общее кратное, это наименьшее положительное число, которое делится нацело на два или более числа. Очень удобно, что существует формула для нахождения нока двух чисел. Нод, или наибольший общий делитель, наоборот, это наибольшее число, которое делит два или более числа без остатка. Также есть алгоритм для нахождения нода, который основан на простых числах. Очень интересно, как эти понятия могут применяться в повседневной жизни. Например, при расчете времени, когда необходимо найти общий множитель для двух периодов, или при решении задач на скорость и расстояние. В целом, статья была очень понятной и полезной. Я теперь лучше понимаю, что такое нок и нод в математике и как их можно применять на практике. Спасибо за разъяснения!
Статья очень понятно объясняет, что такое НОК (наименьшее общее кратное) и НОД (наибольший общий делитель). Я всегда путала эти понятия, но теперь все стало ясно. НОК — это наименьшее число, которое делится на все заданные числа без остатка, а НОД — это наибольшее число, которое делит все заданные числа без остатка. Эти понятия очень полезны в математике, особенно при работе с дробями. Теперь я смогу легко находить НОК и НОД чисел, благодаря этой статье. Очень рекомендую ее прочитать всем, кто хочет разобраться в этих понятиях!
Всегда интересно погрузиться в мир математики и разобраться в таких понятиях, как нок и нод. Несмотря на то, что они имеют схожие названия, их значения и применение сильно отличаются друг от друга. Нод, или наибольший общий делитель, позволяет нам находить общие делители двух чисел. Это очень полезно при решении различных задач, например, при сокращении дробей. Нок, или наименьшее общее кратное, наоборот, позволяет нам находить наименьшее число, которое делится на оба заданных числа. Это выгодно при работе с дробями или при решении задач, связанных с периодичностью. В итоге, понимание разницы между нок и нод поможет нам более глубоко понять и применять математические концепции в нашей повседневной жизни.