Что такое калька в математике

Калька в математике – это процесс построения нового объекта путем копирования исходного объекта с сохранением его формы и размеров. Узнайте, как применяется калька в различных областях математики и какие методы используются для создания копии объекта.

Калька – это один из важных понятий в математике, которое играет ключевую роль в изучении функций и их производных. Калька является математическим инструментом, который используется для анализа и описания поведения функций в окрестности определенной точки. Она позволяет определить изменение функции при бесконечно малом приращении аргумента.

Калька представляет собой предел отношения приращения функции к приращению аргумента при стремлении приращения аргумента к нулю. В математической нотации кальку обозначают символом dx, который означает бесконечно малую величину приращения аргумента.

Например, пусть у нас есть функция f(x), а x0 – точка, в которой мы хотим рассмотреть поведение функции. Тогда кальку функции f(x) в точке x0 можно определить следующим образом: f'(x0) = lim(dx→0) (f(x0+dx) — f(x0))/dx, где f'(x0) – производная функции f(x) в точке x0.

Калька имеет несколько основных свойств, которые позволяют удобно исследовать функции и их производные. Одно из основных свойств кальки – линейность. Это означает, что калька суммы функций равна сумме калек этих функций. Кроме того, существует правило кальки произведения, которое позволяет находить кальку произведения двух функций.

Примеры использования кальки в математике могут быть разнообразными. Она позволяет находить точку экстремума функции, определять ее выпуклость и вогнутость, а также исследовать различные аспекты поведения функции. Калька является неотъемлемой частью математического анализа и необходимым инструментом для решения многих задач в различных областях науки и техники.

Калька в математике: определение, основные свойства и примеры

Основные свойства кальки:

• Калька позволяет обобщать и расширять существующие математические концепции и результаты.
• Она помогает устанавливать связи и аналогии между различными областями математики.
• Калька способствует упрощению и систематизации математических идей и результатов.
• Она позволяет применять известные методы и техники для решения новых задач в других областях математики.

Примеры кальки:

1. Применение идей и методов из геометрии для решения задач в алгебре.
2. Использование идей и результатов из комбинаторики для анализа вероятностных моделей.
3. Перенос методов и техник из математического анализа для изучения дифференциальных уравнений.

Калька является важным инструментом в развитии и прогрессе математики, позволяя исследователям использовать уже известные концепции и результаты для решения новых и сложных задач.

Калька в математике: определение и основные понятия

Калька является одним из основных методов решения математических задач и обладает рядом важных свойств:

1. Сохранение структуры: при кальке сохраняется структура математического объекта или его свойства. Например, если в исходной области определены операции сложения и умножения, то при кальке эти операции также будут определены в целевой области.
2. Сохранение свойств: калька позволяет сохранить свойства объекта или его характеристики при переносе из одной области в другую. Например, если в исходной области присутствует коммутативность операции сложения, то она будет сохранена и в целевой области.
3. Сохранение отношений: калька позволяет сохранить отношения между объектами или их характеристиками при переносе из одной области в другую. Например, если в исходной области два числа являются равными, то и в целевой области они также будут равными.

Примером применения кальки в математике может служить процесс нахождения производной функции. Здесь исходная функция является объектом, а производная – его свойством. Путем применения процесса кальки к функции, можно найти ее производную без искажения структуры и свойств исходной функции.

Основные свойства кальки в математике

Основные свойства кальки в математике включают:

1. Линейность: Калька удовлетворяет свойству линейности, что означает, что сумма двух кальок равна кальке от суммы. То есть, если f(x) и g(x) — функции, и a и b — константы, то:

∫(a*f(x) + b*g(x))dx = a*∫f(x)dx + b*∫g(x)dx

2. Интегрирование по частям: Калька позволяет использовать метод интегрирования по частям для разложения сложной функции на произведение двух более простых функций. Формула интегрирования по частям имеет вид:

∫u(x)*v'(x)dx = u(x)*v(x) — ∫v(x)*u'(x)dx

3. Замена переменной: Калька позволяет использовать метод замены переменной для упрощения интегрирования. Формула замены переменной имеет вид:

∫f(u(x))*u'(x)dx = ∫f(u)du

Основные свойства кальки в математике помогают упростить и ускорить решение математических задач, а также сделать их более понятными и наглядными. Они являются основой для дальнейшего изучения и применения кальки в различных областях науки и техники.

Примеры использования кальки в математике

ПримерОписание

Определение скорости	Калька позволяет определить мгновенную скорость объекта в заданный момент времени. Для этого используется понятие производной функции, которая описывает зависимость пройденного пути от времени.
Нахождение экстремумов функции	С помощью кальки можно найти точки локального минимума или максимума функции. Для этого используется понятие производной функции и ее нулей.
Решение дифференциальных уравнений	Калька позволяет решать дифференциальные уравнения, которые описывают зависимость одной или нескольких переменных от их производных. Это широко применяется в физике, химии и других естественных науках.
Исследование функций	Калька позволяет исследовать различные свойства функций, такие как выпуклость, точки перегиба, асимптоты и другие. Для этого используются производная и вторая производная функции.

Это лишь некоторые примеры использования кальки в математике. Дифференциальное исчисление имеет множество приложений и играет важную роль в понимании и анализе различных явлений и процессов.

Калька в математике: применение в различных областях

1. Интегралы и производные. Калька позволяет находить площади фигур, определять скорость изменения функций, решать уравнения и многое другое. Она является неотъемлемой частью математического анализа.
2. Физика. Калька широко используется в физике для моделирования и анализа различных явлений. Она позволяет решать задачи по движению тел, определению силы, работы и энергии.
3. Экономика. Калька играет важную роль в экономических исследованиях, позволяя анализировать спрос и предложение, определять оптимальные решения, прогнозировать будущие тенденции и многое другое.
4. Статистика. Калька используется для анализа данных и построения математических моделей. Она помогает определять вероятности, строить графики, проводить статистические исследования и т.д.
5. Инженерия. В инженерных расчетах калька применяется для определения оптимальных параметров конструкций, моделирования и анализа систем, решения задач механики и многое другое.

Таким образом, калька является важным инструментом в математике и находит широкое применение в различных областях науки и практики.

Значимость кальки в математике

Одним из основных свойств кальки является связь между производной и интегралом функции. Так, производная функции показывает ее скорость изменения в каждой точке, а интеграл функции представляет собой обратную операцию, восстанавливающую функцию по ее скорости изменения.

Калька также позволяет решать различные задачи, связанные с изменением величин во времени. Например, она широко применяется в физике для решения задач динамики, где величины меняются с течением времени.

Примером использования кальки в математике может быть нахождение площади фигуры, ограниченной кривой. Для этого можно использовать интеграл, который позволяет найти площадь под кривой.

Таким образом, калька является мощным инструментом в математике, который позволяет анализировать функции и их свойства, решать задачи и находить площади фигур. Она играет важную роль в различных областях науки и техники.

Интегралы и производные как основные элементы кальки

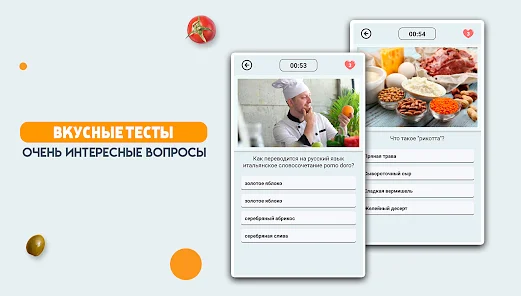
Производная функции показывает, как быстро функция меняется в каждой точке своего определения. Она является мерой скорости изменения функции и определяется как предел отношения приращения функции к приращению ее аргумента при стремлении приращения аргумента к нулю.

Интеграл функции, в свою очередь, является обратной операцией к производной. Он позволяет найти площадь под кривой графика функции или найти значение функции, зная ее производную.

Интегралы и производные связаны между собой формулой Ньютона-Лейбница, которая устанавливает, что интеграл функции является первообразной этой функции, то есть ее антипроизводной. Таким образом, интеграл функции позволяет восстановить саму функцию по ее производной.

Интегралы и производные широко применяются в различных областях математики, физики, экономики и других науках. Они являются основными инструментами для моделирования и анализа различных явлений и процессов.

Вопрос-ответ:

Что такое калька в математике?

Калька в математике — это процесс переноса или копирования геометрических фигур или их свойств на другую поверхность без изменения их формы или размеров.

Какие основные свойства имеет калька в математике?

Основные свойства кальки в математике включают сохранение формы и размеров фигуры при переносе или копировании, а также сохранение геометрических свойств, таких как углы, прямые и параллельные линии.

Можете привести примеры использования кальки в математике?

Калька может использоваться в математике для построения симметричных фигур относительно оси, для копирования углов или отрезков, а также для нахождения точек пересечения прямых или окружностей.

Как калька связана с геометрией?

Калька имеет прямое отношение к геометрии, так как она позволяет переносить и копировать геометрические фигуры и их свойства на другие поверхности. Это помогает в решении различных геометрических задач и построении точных геометрических фигур.

Как калька может быть полезна в повседневной жизни?

Калька может быть полезна в повседневной жизни для создания точных копий геометрических фигур или для переноса их свойств на другие поверхности. Например, она может использоваться при создании макетов, дизайне интерьера или строительстве.

Видео по теме: