Производные как решать высшая математика
Содержимое
- 1 Производные как решать высшая математика
- 1.1 Основные определения и принципы вычисления производных
- 1.2 Методы нахождения производных сложных функций
- 1.3 Примеры применения производных в экономике и физике
- 1.4 Решение задач оптимизации с использованием производных
- 1.5 Производные и графики функций: анализ поведения функций
- 1.6 Видео по теме:
- 1.7 Вопрос-ответ:
- 1.8 Производные высших порядков и их применение
- 1.9 Практические рекомендации по самостоятельному решению примеров производных
Узнайте, как решать задачи по высшей математике, связанные с производными. Изучите основные методы и приемы решения, чтобы успешно справиться с этой сложной математической темой.
Производные являются одним из ключевых понятий в высшей математике. Они позволяют определить скорость изменения функции в каждой ее точке и решать широкий спектр задач. Понимание методов решения примеров производных является неотъемлемой частью математической подготовки студентов, изучающих высшие научные дисциплины.
В данном руководстве мы рассмотрим основные приемы решения примеров производных. Мы начнем с общего понятия производной функции и далее перейдем к определению производной различных элементарных функций. Затем мы изучим правила дифференцирования сложных функций и рассмотрим основные методы вычисления производных.
Важно отметить, что решение примеров производных требует хорошего понимания математических операций, правил алгебры и тригонометрии. Поэтому перед тем, как приступить к решению примеров производных, рекомендуется повторить основные математические понятия и приемы. Кроме того, практика является неотъемлемой частью освоения данного материала, поэтому рекомендуется решать как можно больше примеров для закрепления навыков.
В конце руководства представлены практические задания с подробными пошаговыми решениями и ответами. Решение данных задач позволит вам проверить свои знания и умения в решении примеров производных. Мы надеемся, что данное руководство поможет вам освоить методы решения примеров производных и применить их в практических задачах из области прикладной математики и физики.
Основные определения и принципы вычисления производных
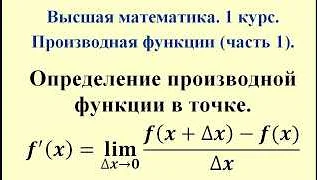
В основе вычисления производной лежит понятие предела. Для функции f(x) ее производная в точке x = a (обозначается f'(a) или dy/dx|x=a) определяется следующим образом:
Производная функции f(x) в точке x = a равна пределу отношения приращения функции к приращению аргумента при стремлении приращения аргумента к нулю:
f'(a) = limh->0 (f(a + h) — f(a))/h
Другими словами, производная функции в точке a определяется как предел отношения приращения функции к приращению аргумента, когда приращение аргумента стремится к нулю.
Чтобы вычислить производную функции, нужно использовать различные правила дифференцирования. Некоторые из основных правил включают:
- Правило линейности: производная суммы функций равна сумме производных функций;
- Правило произведения: производная произведения функций равна произведению производной первой функции на вторую функцию плюс первая функция умноженная на производную второй функции;
- Правило частного: производная частного функций равна разности производной первой функции умноженной на вторую функцию и первой функции умноженной на производную второй функции, все деленное на квадрат второй функции;
- Правило композиции: производная сложной функции равна произведению производной внешней функции на производную внутренней функции.
Принципы вычисления производных также включают правило многократной дифференциации, правило вычисления производной обратной функции и основные производные элементарных функций.
Вычисление производных позволяет нам анализировать функции, искать экстремумы, находить наклон кривых, решать оптимизационные задачи и многое другое. Понимание основных определений и принципов вычисления производных является фундаментальным для успешного изучения и применения дифференциального исчисления в высшей математике.
Методы нахождения производных сложных функций
Один из методов нахождения производных сложных функций — это метод дифференцирования по формуле производной композиции функций. Суть этого метода заключается в применении правила дифференцирования для композиции функций, которое гласит: если функция y(x) представляется в виде композиции двух функций u(v(x)), то производная y'(x) этой функции может быть найдена по формуле: y'(x) = u'(v(x)) * v'(x). Этот метод позволяет находить производные сложных функций, используя уже известные производные базовых функций.
Еще один метод нахождения производных сложных функций — это метод дифференцирования по формуле производной обратной функции. Если у функции y(x) существует обратная функция x(y), то производная обратной функции может быть найдена по формуле: (d/dy) x(y) = 1 / (dy/dx). Этот метод позволяет находить производные обратных функций, а затем и производные сложных функций с использованием уже известных производных базовых функций.
Существуют и другие методы нахождения производных сложных функций, такие как метод дифференцирования по правилам элементарных функций, метод дифференцирования по правилам трансцендентных функций и др. Каждый из этих методов имеет свои особенности и применяется в различных ситуациях для нахождения производных сложных функций.
МетодОписание
| Метод дифференцирования по формуле производной композиции функций | Применение правила дифференцирования для композиции функций |
| Метод дифференцирования по формуле производной обратной функции | Нахождение производной обратной функции |
| Метод дифференцирования по правилам элементарных функций | Применение правил дифференцирования для элементарных функций |
| Метод дифференцирования по правилам трансцендентных функций | Применение правил дифференцирования для трансцендентных функций |
Выбор метода нахождения производных сложных функций зависит от конкретной задачи и доступных производных базовых функций. Важно уметь применять различные методы для решения задач и получения точных результатов.
Примеры применения производных в экономике и физике

В экономике производные используются для определения оптимальных решений в различных ситуациях. Например, при анализе производственной функции, производная позволяет найти максимум или минимум функции, что позволяет определить оптимальное количество производства и максимальную прибыль компании. Кроме того, производные применяются при изучении спроса и предложения, позволяя определить эластичность этих показателей и прогнозировать изменения в рыночной ситуации.
В физике производные используются для описания движения тел, изменения физических величин и определения законов природы. Например, производная позволяет определить скорость изменения положения тела, ускорение, момент инерции и другие параметры. Производные также применяются при решении задач на определение экстремумов функций, что позволяет оптимизировать процессы и моделировать поведение системы.
Применение производных в экономике и физике является примером того, как математические понятия могут быть применимы в реальных ситуациях. Изучение производных позволяет анализировать и прогнозировать различные процессы, оптимизировать решения и моделировать сложные системы. Поэтому знание производных является необходимым инструментом для специалистов в области экономики и физики.
Решение задач оптимизации с использованием производных

Производная функции показывает ее скорость изменения в каждой точке. Если производная положительна в точке, то функция возрастает, если производная отрицательна, то функция убывает. Кроме того, экстремумы функции (максимумы и минимумы) находятся в точках, где производная равна нулю или не существует.
Для решения задач оптимизации с использованием производных необходимо выполнить следующие шаги:
- Найти производную функции.
- Найти критические точки, решив уравнение производной равной нулю или не существует.
- Проверить, являются ли найденные критические точки максимумами или минимумами, используя вторую производную.
- Найти значение функции в найденных точках и сравнить их для определения глобального экстремума.
Применение производных в задачах оптимизации позволяет эффективно находить оптимальные значения функций в различных областях, таких как экономика, физика, инженерия и другие. Знание методов решения задач оптимизации с использованием производных является важным инструментом для анализа и оптимизации различных процессов и систем.
Производные и графики функций: анализ поведения функций

Для начала анализа поведения функции необходимо вычислить ее производную. Производная функции показывает, как изменяется функция в каждой точке. Значение производной в точке позволяет определить наклон касательной к графику функции в этой точке.
Исследование функции включает в себя нахождение всех точек, в которых производная функции равна нулю или не существует. Эти точки называются критическими точками функции. Именно в этих точках происходят экстремумы функции.
Определение знака производной на интервалах между критическими точками позволяет определить возрастание или убывание функции на каждом интервале. Если производная положительна на интервале, то функция возрастает. Если производная отрицательна, то функция убывает.
График функции позволяет визуализировать ее поведение на оси координат. Анализ графика функции помогает увидеть основные характеристики функции, такие как точки экстремума, точки перегиба, асимптоты и другие особенности.
Исследование поведения функций с помощью производных и графиков является важным инструментом в высшей математике. Оно позволяет строить модели и анализировать различные явления и процессы в естественных и социальных науках.
Видео по теме:
Вопрос-ответ:
Какие основные правила применяются при решении примеров производных в высшей математике?
При решении примеров производных в высшей математике применяются такие основные правила, как правило дифференцирования суммы и разности функций, правило дифференцирования произведения функций, правило дифференцирования частного функций, правило дифференцирования сложной функции, правило дифференцирования обратной функции и правило дифференцирования степенной функции.
В чем состоит правило дифференцирования суммы и разности функций?
Правило дифференцирования суммы и разности функций утверждает, что производная суммы или разности двух функций равна сумме или разности производных этих функций. То есть, если f(x) и g(x) — две функции, то производная их суммы (f(x) + g(x)) равна сумме производных функций f'(x) и g'(x), а производная их разности (f(x) — g(x)) равна разности производных функций f'(x) и g'(x).
Как применять правило дифференцирования произведения функций?
Правило дифференцирования произведения функций утверждает, что производная произведения двух функций равна произведению производной первой функции на вторую функцию и производной второй функции на первую функцию. То есть, если f(x) и g(x) — две функции, то производная их произведения (f(x) * g(x)) равна f'(x) * g(x) + g'(x) * f(x).
Как решать примеры производных сложной функции?
Для решения примеров производных сложной функции применяется правило дифференцирования сложной функции, которое утверждает, что производная сложной функции равна произведению производной внешней функции и производной внутренней функции. То есть, если y = f(g(x)), то производная y по x равна произведению производной f по g и производной g по x, то есть dy/dx = (df/dg) * (dg/dx).
Производные высших порядков и их применение
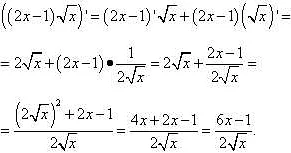
Производные высших порядков определяются аналогично первой производной. Для этого необходимо несколько раз продифференцировать исходную функцию. Например, вторая производная функции f(x) обозначается как f»(x) или d2f/dx2.
Производные высших порядков находят свое применение в различных областях математики и естественных наук. Например, в физике они позволяют описывать движение тела с учетом изменения его ускорения. В экономике производные высших порядков используются для моделирования роста и изменения стоимости товаров и услуг.
Другим важным применением производных высших порядков является определение точек экстремума функции. Экстремумы – это точки, в которых функция достигает своего максимального или минимального значения. Анализ производных высших порядков позволяет определить, является ли точка экстремумом и его тип (максимум или минимум).
Таким образом, производные высших порядков играют важную роль в анализе функций и их применении в различных научных и практических областях. Изучение методов нахождения и использования производных высших порядков позволяет получить более точные и полные решения задач, связанных с изменением функций.
Практические рекомендации по самостоятельному решению примеров производных

1. Понимание основных понятий. Прежде чем решать примеры производных, убедитесь, что вы хорошо понимаете основные понятия, такие как производная, функция, производная функции, пределы и дифференциалы.
2. Ознакомление с правилами дифференцирования. Изучите основные правила дифференцирования, такие как правило суммы, правило произведения, правило частного, правило цепной дроби и т.д. Эти правила будут использоваться для нахождения производной функции.
3. Изучение методов дифференцирования. Ознакомьтесь с различными методами дифференцирования, такими как дифференцирование по формулам, дифференцирование по определению, использование таблицы производных и т.д. Используйте эти методы в зависимости от конкретной задачи.
4. Практика решения многочисленных примеров. Чем больше примеров вы решите, тем лучше вы освоите навык решения примеров производных. Начните с простых примеров и постепенно переходите к более сложным. Практикуйтесь регулярно, чтобы поддерживать навык в хорошей форме.
5. Проверка правильности решения. После решения примера производной всегда проверьте правильность вашего решения. Используйте полученную производную для проверки различных свойств функции, таких как экстремумы, точки перегиба и т.д.
6. Изучение специальных случаев. Изучите специальные случаи, такие как производные степенных функций, тригонометрических функций, логарифмических функций и т.д. Это поможет вам решать более сложные примеры и понимать особенности различных типов функций.
Следуя этим практическим рекомендациям, вы сможете успешно решать примеры производных и расширить свои знания в высшей математике.

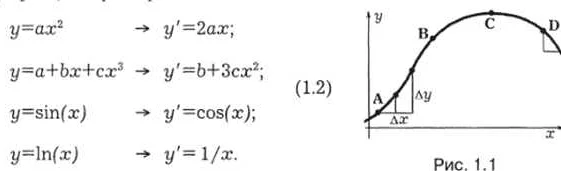

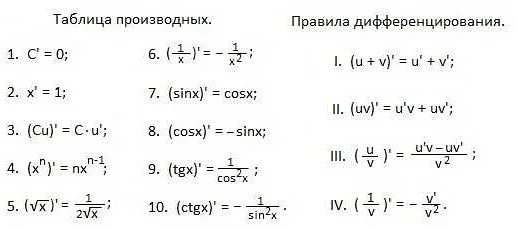
Отличная статья! Очень понятно и доступно объяснено, как решать примеры производных в высшей математике. Я всегда испытывал трудности с этой темой, но благодаря данному материалу все стало намного яснее. Особенно понравилось, что автор дал несколько примеров и пошагово разобрал каждый из них. Теперь я уверен, что смогу справиться с любыми задачами по нахождению производных. Большое спасибо за такую полезную информацию! Рекомендую всем, кто хочет освоить эту тему!
Статья очень понравилась! Она дает полное и практическое руководство по решению примеров производных в высшей математике. Я всегда сталкиваюсь с трудностями при решении таких задач, но благодаря этой статье я стала лучше понимать процесс и методы решения. Очень полезно, что автор пошагово объясняет каждый шаг и дает примеры для практики. Теперь я чувствую, что у меня есть инструменты, чтобы успешно решать примеры производных. Большое спасибо за такую доступную и информативную статью! Я обязательно буду использовать ее в своей учебе.