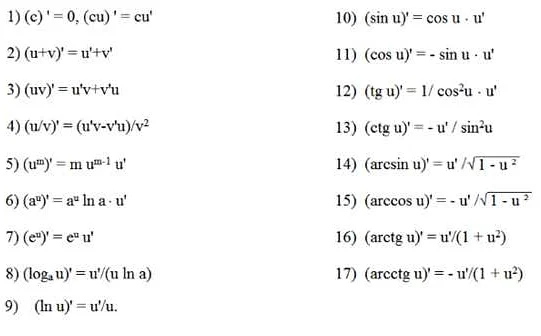Что такое дифференцирование в математике

Дифференцирование в математике — это процесс нахождения производной функции. Оно позволяет определить скорость изменения функции в каждой точке ее графика, а также найти точки экстремума и изучить поведение функции в окрестности этих точек. Дифференцирование является важным инструментом в анализе и оптимизации функций и используется в различных областях науки и техники.

Дифференцирование – один из фундаментальных понятий математического анализа. Оно позволяет изучать локальные изменения функций и их поведение вблизи заданной точки. Дифференцирование активно применяется во многих областях науки, техники и экономики, а также играет важную роль в решении оптимизационных задач. В этой статье мы рассмотрим определение дифференцирования и основные принципы его применения.

Основной идеей дифференцирования является нахождение производной функции – её скорости изменения в каждой точке. Производная функции f(x) в точке x определяется как предел отношения приращения функции к приращению аргумента при бесконечно малом приращении аргумента. Формально, производная f'(x) функции f(x) в точке x вычисляется по следующей формуле: f'(x) = lim(h -> 0) (f(x+h) — f(x))/h.

Дифференцирование позволяет найти не только производную функции в точке, но и решить ряд других задач. Например, с помощью дифференцирования можно находить экстремумы функций – точки минимума и максимума. Для этого необходимо найти точки, в которых производная функции равна нулю или не существует. Дифференцирование также позволяет анализировать поведение функций в окрестности заданной точки и строить графики функций с помощью производных. При изучении функций высших порядков применяется понятие n-ой производной, которое позволяет изучать различные аспекты функции и их изменения.

Дифференцирование – неотъемлемая часть математического анализа и находит широкое применение в различных областях знания. Оно позволяет изучать локальные изменения функций и находить их экстремумы, а также анализировать поведение функций в различных точках. Понимание основных принципов дифференцирования является важным инструментом для решения оптимизационных задач и изучения функций высших порядков. В следующих разделах мы подробнее рассмотрим основные методы дифференцирования и их применение в практике.

Что такое дифференцирование

Для дифференцирования функции необходимо использовать методы и правила дифференцирования, которые позволяют найти производную функции. Основные принципы дифференцирования включают правила дифференцирования элементарных функций, таких как константы, степенные функции, логарифмические и тригонометрические функции. Они позволяют находить производные функций, состоящих из комбинаций этих элементарных функций.

Производная функции показывает, как быстро изменяется функция в каждой точке графика. Она позволяет определить, в какой точке функция имеет максимум или минимум, а также показывает, в каких точках графика функция возрастает или убывает.

Дифференцирование широко применяется в различных областях науки и инженерии. Например, в физике дифференцирование позволяет определить скорость и ускорение тела, а также решать задачи, связанные с движением и изменением состояния системы. В экономике дифференцирование используется для анализа изменений спроса и предложения, определения эластичности и маржинальных ставок.

Зачем нужно дифференцирование

Одним из важных применений дифференцирования является определение экстремумов функций. С помощью дифференцирования мы можем найти точки, в которых функция достигает наибольшего или наименьшего значения. Это позволяет оптимизировать процессы и решать задачи в различных областях, таких как экономика, физика, биология и т.д.

Дифференцирование также играет важную роль в построении графиков функций. Зная производную функции, мы можем определить точки перегиба, максимумы и минимумы, асимптоты и другие свойства графика. Это позволяет нам визуализировать и анализировать поведение функции и делать выводы о её свойствах.

Кроме того, дифференцирование широко применяется в физике для описания процессов, связанных с изменением величин в пространстве и времени. С помощью производных мы можем описывать скорость, ускорение, траектории движения и другие характеристики физических объектов и явлений.

В общем, дифференцирование является мощным инструментом анализа и моделирования различных явлений. Оно позволяет нам получить более полное представление о функциях, их свойствах и поведении, а также использовать эту информацию для решения задач в различных областях науки и техники.

Определение дифференцирования

Дифференцирование является одним из основных понятий математического анализа и имеет широкое применение в различных областях науки, техники и экономики. Оно позволяет изучать свойства функций, находить максимумы и минимумы, а также решать задачи оптимизации.

Дифференцирование основано на понятии предела функции. Производная функции в точке является мерой её изменения в этой точке. Чем больше значение производной, тем быстрее функция меняет своё значение в данной точке.

Для дифференцирования функции необходимо, чтобы функция была дифференцируемой в каждой точке своей области определения. Дифференцируемость функции означает, что функция гладкая и имеет конечную производную в каждой точке. Если функция не является дифференцируемой в какой-то точке, то в этой точке её производная не существует.

Основные понятия и термины

Производная функции является мерой ее изменения в каждой точке и может интерпретироваться как скорость изменения функции или ее наклон касательной в данной точке. Дифференцирование является обратной операцией к интегрированию и позволяет находить первообразную функции.

Важными понятиями в дифференцировании являются:

• Производная — это коэффициент наклона касательной к графику функции в данной точке. Производная функции в точке равна пределу отношения приращения функции и приращения аргумента при стремлении приращения аргумента к нулю.
• Производная первого порядка — это производная функции по одной переменной. Она позволяет найти скорость изменения функции в каждой точке.
• Производная высших порядков — это производные функции по нескольким переменным. Они позволяют найти информацию о кривизне и выпуклости функции.
• Точка экстремума — это точка, в которой производная функции равна нулю или не существует. Точка может быть максимумом, минимумом или точкой перегиба.

Понимание основных понятий и терминов в дифференцировании позволяет более глубоко изучать и понимать свойства функций и их поведение. Они являются основой для решения различных задач и применения в других областях математики и науки в целом.

Производная функции

Производная функции обозначается символом «f'(x)» или «dy/dx». Она может быть представлена как предел отношения приращения функции к приращению аргумента при стремлении приращения аргумента к нулю. Формально, производная функции f(x) в точке x определяется следующим образом:

f'(x) = limh→0 (f(x+h) — f(x)) / h

Интуитивно, производная функции в точке х показывает, насколько быстро значение функции меняется при изменении аргумента на очень малое значение. Если производная положительна, функция возрастает в данной точке, если отрицательна – убывает.

Производная функции позволяет решать различные задачи в математике и физике, такие как определение экстремумов функции, построение касательных и нормалей к графику функции, анализ изменений функций в определенных интервалах и т.д.

Основные принципы дифференцирования

ПринципОписание

Линейность	Производная суммы функций равна сумме производных этих функций. Производная константы равна нулю.
Производная произведения	Производная произведения функций равна произведению производной первой функции на вторую функцию, плюс произведение первой функции на производную второй функции.
Производная частного	Производная частного функций равна разности произведения производной первой функции на вторую функцию и произведения первой функции на производную второй функции, деленной на квадрат второй функции.
Цепное правило	Производная сложной функции равна произведению производной внешней функции на производную внутренней функции.

Знание и применение этих основных принципов позволяет эффективно находить производные функций и использовать их в дальнейших математических рассуждениях и приложениях.

Принципы вычисления производной

Существуют несколько основных принципов, которые позволяют вычислять производные различных функций:

1. Принцип линейности: производная суммы двух функций равна сумме их производных. То есть, если функции f(x) и g(x) имеют производные f'(x) и g'(x) соответственно, то производная их суммы f(x) + g(x) равна f'(x) + g'(x).
2. Принцип произведения: производная произведения двух функций равна произведению производной одной функции на другую и производной другой функции на одну. То есть, если функции f(x) и g(x) имеют производные f'(x) и g'(x) соответственно, то производная их произведения f(x) * g(x) равна f'(x) * g(x) + f(x) * g'(x).
3. Принцип частного: производная частного двух функций равна разности произведения производной одной функции на другую и произведения производной другой функции на одну, деленной на квадрат второй функции. То есть, если функции f(x) и g(x) имеют производные f'(x) и g'(x) соответственно, то производная их частного f(x) / g(x) равна (f'(x) * g(x) — f(x) * g'(x)) / g^(2)(x).
4. Принцип сложной функции: производная сложной функции равна произведению производной внешней функции по внутренней переменной на производную внутренней функции по ее переменной. То есть, если функция f(u) имеет производную f'(u), а функция u(x) имеет производную u'(x), то производная сложной функции f(u(x)) равна f'(u) * u'(x).

С помощью этих принципов можно вычислять производные самых различных функций, что позволяет анализировать их поведение и применять в различных областях науки и техники.

Принципы определения касательной

Существуют два основных принципа определения касательной:

1. Геометрический принцип:

Геометрический принцип заключается в том, что касательная к графику функции в определенной точке является предельным положением секущей, проходящей через эту точку, приближающейся к данной точке. Точка касания является пределом точек пересечения секущей с графиком функции при уменьшении расстояния между точками секущей.

2. Аналитический принцип:

Аналитический принцип основан на использовании производной функции в данной точке. Касательная к графику функции в точке (а, f(a)) имеет ту же производную, что и сама функция, в этой точке. То есть, касательная задается уравнением y = f'(a)(x — a) + f(a), где f'(a) — производная функции в точке a.

Таким образом, принципы определения касательной позволяют нам точно определить линию, касающуюся графика функции в определенной точке и отображающую изменение функции в этой точке.

Вопрос-ответ:

Что такое дифференцирование?

Дифференцирование — это одно из основных понятий математического анализа, которое позволяет находить производную функции в каждой точке ее области определения. Производная функции показывает, как быстро меняется значение функции в данной точке.

Зачем нужно дифференцирование в математике?

Дифференцирование играет важную роль в математике и ее приложениях. Оно позволяет находить скорости изменения величин, находить экстремумы функций, решать оптимизационные задачи, а также исследовать графики функций и их поведение в окрестности точек.

Какие основные принципы лежат в основе дифференцирования?

Основными принципами дифференцирования являются линейность, правило производной суммы и производной произведения, а также правило дифференцирования сложной функции (правило цепочки). Эти принципы позволяют находить производную функции по правилам алгебры и элементарной функции.

Как найти производную сложной функции?

Для нахождения производной сложной функции применяется правило дифференцирования сложной функции, или правило цепочки. Суть этого правила заключается в последовательном дифференцировании внешней и внутренней функций, а затем их перемножении.

Какие приложения имеет дифференцирование в реальной жизни?

Дифференцирование имеет широкие приложения в различных областях, таких как физика, экономика, биология и технические науки. Например, оно используется для моделирования движения тел, оптимизации производственных процессов, анализа роста популяций и многое другое.

Что такое дифференцирование?

Дифференцирование — это одна из основных операций математического анализа, которая позволяет находить производную функции в каждой точке ее области определения. Производная функции показывает, как быстро меняется значение функции в данной точке.

Принципы применения в задачах

ПринципОписание

Принцип дифференцирования суммы	Позволяет находить производную суммы двух функций путем нахождения производных каждой функции по отдельности и их сложения.
Принцип дифференцирования произведения	Позволяет находить производную произведения двух функций путем использования правила производной произведения и нахождения производных каждой функции по отдельности.
Принцип дифференцирования сложной функции	Позволяет находить производную сложной функции путем использования правила дифференцирования сложной функции и нахождения производных внутренней и внешней функций.
Принцип дифференцирования частного	Позволяет находить производную частного двух функций путем использования правила дифференцирования частного и нахождения производных числителя и знаменателя.
Принцип дифференцирования обратной функции	Позволяет находить производную обратной функции путем использования правила дифференцирования обратной функции и нахождения производной исходной функции.

Эти принципы являются основой для решения различных задач, связанных с дифференцированием. Их применение позволяет находить производные функций, а также решать задачи оптимизации, находить экстремумы функций и исследовать поведение функций в различных точках.

Видео по теме: