Знакомство с классами чисел в математике для учеников 4 класса
Содержимое
Классы чисел в математике 4 класс: понятие, виды и примеры. Узнайте, как рассматриваются натуральные, целые, рациональные и другие классы чисел на уровне начальной школы.
В математике 4 класса важно понимать, что числа можно разделить на разные классы в зависимости от их особенностей и свойств. Знание классов чисел помогает ребятам правильно выполнять различные задания и решать математические примеры.
Наиболее распространенный класс чисел — натуральные числа. Они включают все положительные числа, начиная с единицы. Натуральные числа используются в различных ситуациях, например, при счете предметов или людей. Важно понимать, что натуральные числа не содержат нуля и отрицательных чисел.
Еще один класс чисел — целые числа. Они включают все натуральные числа, а также их отрицательные значения и ноль. Целые числа используются, когда нужно обозначить отрицательные значения или отсутствие предметов.
Рациональные числа — это числа, которые можно представить в виде дроби, где числитель и знаменатель являются целыми числами. Рациональные числа включают в себя как конечные, так и периодические десятичные дроби. Они используются в различных ситуациях, включая деление, анализ данных и измерения.
Наконец, существуют еще два класса чисел — иррациональные и вещественные числа. Иррациональные числа не могут быть представлены в виде дроби и имеют бесконечное количество десятичных знаков без периода. Вещественные числа включают как рациональные, так и иррациональные числа. Они используются для точных измерений и расчетов.
Определение классов чисел
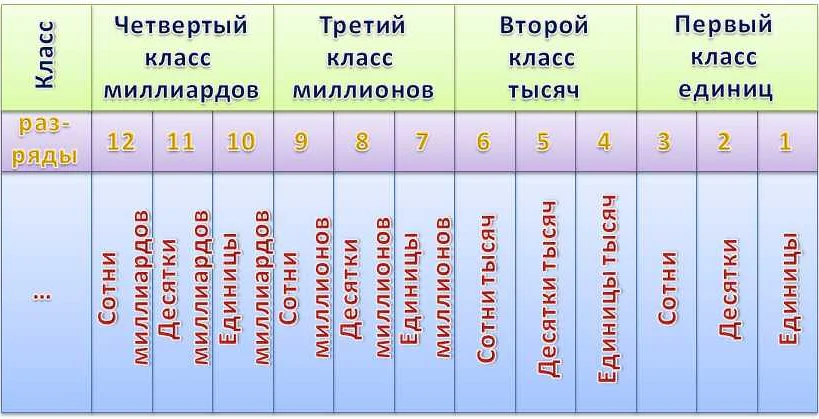
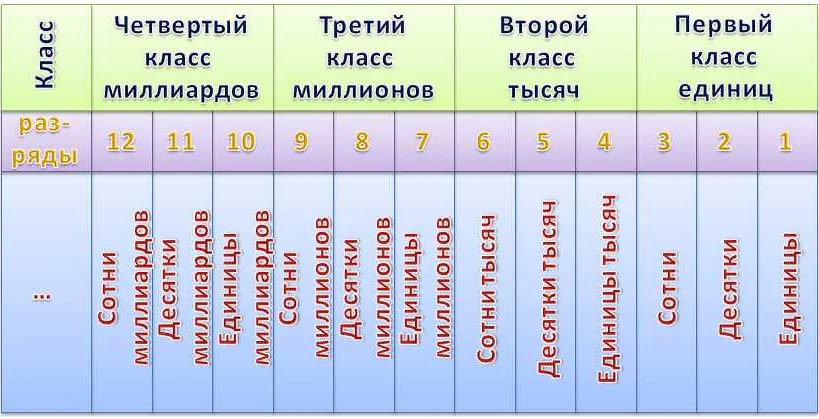
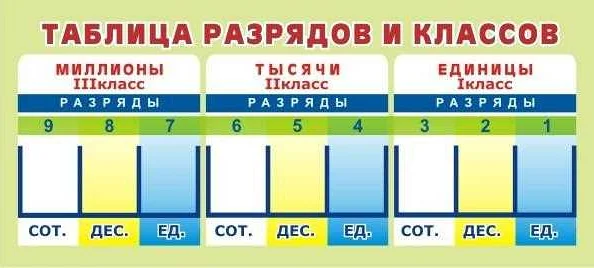
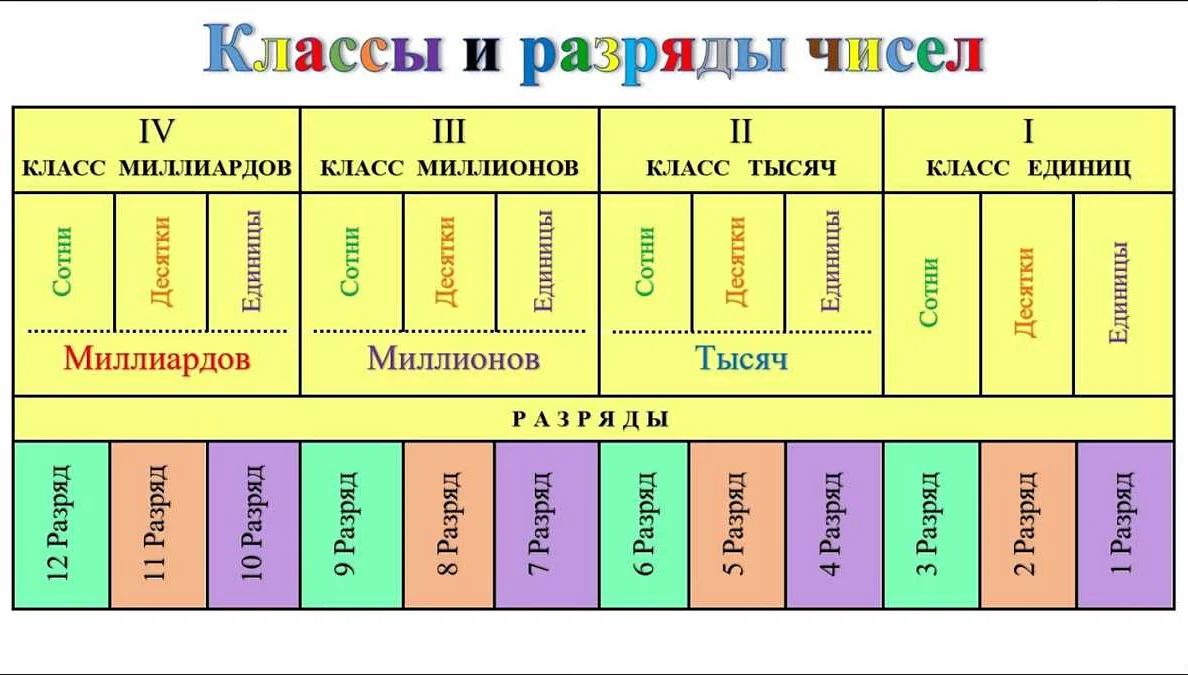
Классы чисел в математике позволяют разделить числа на группы в зависимости от их свойств и особенностей. В четвертом классе изучаются основные классы чисел: натуральные числа, целые числа и рациональные числа.
Натуральные числа (обозначаются символом N) включают все положительные целые числа, начиная с единицы (1, 2, 3, 4, …).
Целые числа (обозначаются символом Z) включают все натуральные числа, их противоположности (отрицательные числа) и ноль (…, -3, -2, -1, 0, 1, 2, 3, …).
Рациональные числа (обозначаются символом Q) включают все числа, которые можно представить в виде дроби, где числитель и знаменатель являются целыми числами (например, 1/2, -3/4, 7/5).
Классы чисел помогают упорядочить и систематизировать числовые значения, а также проводить операции с числами в соответствии с их классом.
Видео по теме:
Натуральные числа

Натуральные числа обозначаются символом N и записываются в виде N = {1, 2, 3, 4, …}. Они используются для подсчета количества предметов, людей, дней недели и т. д. Использование натуральных чисел помогает нам сориентироваться в окружающем мире и проводить различные математические операции.
Натуральные числа имеют несколько свойств:
СвойствоОписание
| Порядок | Натуральные числа упорядочены по возрастанию: 1, 2, 3, … |
| Непрерывность | Между любыми двумя натуральными числами всегда можно найти еще одно натуральное число. |
| Бесконечность | Натуральные числа не имеют верхней границы и продолжаются до бесконечности. |
В математике мы также используем натуральные числа для выполнения различных операций, таких как сложение, вычитание, умножение и деление. Например, с помощью натуральных чисел мы можем подсчитать, сколько всего предметов у нас есть, если у нас есть два ящика с яблоками, а в каждом ящике по 3 яблока.
Таким образом, натуральные числа играют важную роль в математике и используются для подсчета количества предметов и выполнения различных операций.
Целые числа
Множество целых чисел включает в себя натуральные числа, нуль и отрицательные числа. Натуральные числа — это положительные числа, начиная с единицы.
Целые числа можно представить на числовой прямой, где положительные числа располагаются справа от нуля, а отрицательные числа — слева от нуля. Ноль является центром числовой прямой.
Целые числа можно складывать, вычитать, умножать и делить. При сложении двух целых чисел можно получить положительное, отрицательное или нулевое число. При вычитании одного целого числа из другого также может получиться положительное, отрицательное или нулевое число. Умножение целых чисел может давать положительное или отрицательное число, а деление — положительное или отрицательное дробное число.
Например, целые числа 5 и -3 можно сложить следующим образом: 5 + (-3) = 2. Результат сложения положительного числа 5 и отрицательного числа -3 будет положительным числом 2.
Целые числа играют важную роль в математике и применяются в различных областях науки, техники и экономики.
Вопрос-ответ:
Что такое классы чисел?
Классы чисел — это группы чисел, которые имеют общие свойства и особенности. В математике выделяют несколько классов чисел, таких как натуральные, целые, рациональные и дробные числа.
Какие классы чисел существуют в математике для 4 класса?
В математике для 4 класса обычно изучаются такие классы чисел, как натуральные числа (1, 2, 3, и т.д.), целые числа (…, -3, -2, -1, 0, 1, 2, 3, …) и десятичные дроби.
Какие свойства имеют натуральные числа?
Натуральные числа — это положительные целые числа, начиная с 1 (1, 2, 3, и т.д.). Они обладают такими свойствами, как возможность увеличения на единицу (натуральное число n+1), сравнение чисел по величине (больше или меньше), а также сложение и умножение.
Что такое целые числа?
Целые числа — это числа, которые включают в себя натуральные числа, их противоположности и ноль. Они обозначаются символом Z. Целые числа включают положительные и отрицательные числа, а также ноль (…, -3, -2, -1, 0, 1, 2, 3, …).
Что такое десятичные дроби?
Десятичные дроби — это числа, которые записываются с помощью десятичной системы счисления. Они состоят из цифр от 0 до 9 и десятичной запятой. Десятичные дроби могут быть как положительными, так и отрицательными (например, 0,5 или -0,75).
Какие классы чисел существуют в математике для 4 класса?
В математике для 4 класса существуют следующие классы чисел: натуральные числа, целые числа, рациональные числа и вещественные числа.
Рациональные числа
Дроби, которые представляют рациональные числа, могут быть положительными или отрицательными. Например, 1/2, -3/4, 5/8 — все они являются рациональными числами.
Рациональные числа могут быть представлены в виде десятичной дроби, но в некоторых случаях десятичная запись может быть бесконечной и повторяющейся. Например, число 1/3 в десятичной записи будет выглядеть как 0.33333…
Рациональные числа обладают свойствами сложения, вычитания, умножения и деления. Они также образуют упорядоченное множество, что означает, что их можно сравнивать и упорядочивать.
Примеры рациональных чисел
| 1/2 |
| -3/4 |
| 5/8 |
Рациональные числа играют важную роль в математике и находят применение в различных областях, таких как финансы, наука, инженерия и другие.
Иррациональные числа
Примеры иррациональных чисел включают в себя числа π (пи), √2 (корень из 2), и → (золотое сечение). Эти числа являются бесконечными десятичными дробями, которые не имеют повторяющихся или периодических цифр.
Иррациональные числа могут быть представлены в виде бесконечных десятичных дробей, либо в виде корней из натуральных чисел. Например, число √2 можно представить как корень из числа 2. Однако, такие представления не могут быть точными и всегда будут приближенными.
Иррациональные числа имеют множество интересных свойств и используются во многих областях математики, включая геометрию, теорию вероятности и физику.
Примечание: Иррациональные числа обычно обозначаются символом ℜ (Q), который отличается от символа рациональных чисел ℚ (P).
Действительные числа

Множество действительных чисел обозначается символом ℝ. Оно включает в себя все числа на числовой прямой, начиная от отрицательной бесконечности и до положительной бесконечности. Все рациональные числа и иррациональные числа расположены на числовой прямой без пропусков.
Действительные числа можно складывать, вычитать, умножать и делить. Операции над действительными числами подчиняются основным законам алгебры, таким как коммутативность, ассоциативность и дистрибутивность.
Действительные числа используются в различных областях математики, науки и повседневной жизни. Они позволяют точно измерять величины и делать математические вычисления. Например, действительные числа используются при решении задач финансового анализа, физических расчетов, статистических исследований и т.д.
Типы действительных чиселПримеры
| Натуральные числа | 1, 2, 3, 4, … |
| Целые числа | … -3, -2, -1, 0, 1, 2, 3, … |
| Рациональные числа | 1/2, -3/4, 0.25, … |
| Иррациональные числа | Пи (π), корень из 2 (√2), … |
Комплексные числа
Комплексные числа могут быть представлены в виде пар (a, b), где a — действительная часть, а b — мнимая часть. Действительная часть обозначается Re(z), а мнимая часть — Im(z).
Сумма двух комплексных чисел z1 = a1 + b1i и z2 = a2 + b2i определяется как z1 + z2 = (a1 + a2) + (b1 + b2)i.
Умножение двух комплексных чисел z1 и z2 определяется по формуле: z1 * z2 = (a1a2 — b1b2) + (a1b2 + a2b1)i.
Для работы с комплексными числами используются различные математические операции, включая сложение, вычитание, умножение и деление.
Примеры чисел в каждом классе

В математике существуют различные классы чисел, каждый из которых характеризуется определенными свойствами и особенностями. Вот некоторые примеры чисел в каждом классе:
Класс чиселПримеры чисел
| Натуральные числа | 1, 2, 3, 4, 5, … |
| Целые числа | 0, -1, -2, -3, -4, … |
| Рациональные числа | 1/2, -3/4, 0.25, -1.75, … |
| Иррациональные числа | √2, π, e, … |
| Действительные числа | 1, -2, 0.5, √2, π, … |
Это лишь некоторые примеры чисел в каждом классе. В математике существует множество других числовых классов, каждый из которых имеет свои особенности и применения.


Очень интересная статья! Я всегда задавалась вопросом, что такое классы чисел в математике. Теперь все стало ясно. Оказывается, классы чисел — это группы чисел, которые имеют какие-то общие свойства или характеристики. Знание классов чисел позволяет лучше понимать и работать с числами. Например, в статье упоминаются классы натуральных, целых и дробных чисел. Теперь я знаю, что натуральные числа — это числа, которые используются для счета предметов, а целые числа — это числа, которые включают в себя натуральные числа и их отрицания. Очень интересно узнать, что числа могут быть поделены на классы и как они взаимосвязаны. Спасибо за четкое и доступное объяснение! Теперь я понимаю, что классы чисел — это основа для дальнейшего изучения математики. Буду ждать новых статей на эту тему!
Спасибо за это интересное объяснение! Я как родитель никогда не задумывалась о классах чисел в математике. Теперь я понимаю, что это очень важно для развития моего ребенка. Я с нетерпением жду, чтобы поделиться этим новым знанием с ним и помочь ему понять, как классифицировать числа. Это отличная возможность обсудить с ним, что такое натуральные числа, целые числа и дроби. Теперь я уверена, что смогу объяснить все это ему простыми и понятными словами. Эта статья действительно открыла мне глаза и помогла осознать, что классы чисел — это основа для дальнейшего обучения математике. Я благодарна автору за такое подробное объяснение и за возможность стать лучшим родителем для своего ребенка.
Спасибо за интересную и познавательную статью о классах чисел в математике для четвертого класса! Я, как родитель, всегда стараюсь поддерживать интерес своего ребенка к учебе, особенно в математике. Чтение вашей статьи помогло мне лучше понять, что такое классы чисел и как они классифицируются. В статье я нашел простое и понятное объяснение каждого класса чисел: натуральные, целые, рациональные и дроби. Также было интересно узнать, что каждый класс чисел имеет свои особенности и правила, которые нужно знать и применять при решении задач. Очень понравился пример с классификацией чисел по ингредиентам пиццы. Это забавное сравнение помогло мне лучше запомнить, какие числа относятся к определенному классу. Я также хотел бы отметить, что ваша статья была написана доступным и легким языком, что очень важно для детей четвертого класса. Надеюсь, что вы продолжите публиковать подобные материалы, которые помогут детям лучше понять и увлечься математикой. Большое спасибо!