Что такое комбинаторика в математике простыми словами
Содержимое
Комбинаторика — это раздел математики, который изучает методы и правила подсчета и организации объектов или событий. В данной статье вы узнаете, что такое комбинаторика и какие простые слова позволяют легко понять ее основные понятия и принципы.
Комбинаторика – это раздел математики, который изучает способы и правила счета и комбинирования объектов. В комбинаторике рассматриваются различные комбинации, перестановки, подмножества и другие комбинаторные структуры. Этот раздел математики находит применение во многих областях, таких как криптография, компьютерная наука, теория игр, статистика и даже в повседневной жизни.
Основная задача комбинаторики заключается в том, чтобы определить количество возможных комбинаций или вариантов выбора. Для решения этих задач используются различные методы, такие как правило произведения, правило суммы, различные формулы и алгоритмы. Комбинаторика позволяет систематизировать задачи, связанные с выбором и расположением объектов, и находить точные решения на основе математических закономерностей.
Например, представим, что у нас есть 5 разных фруктов – яблоко, груша, банан, апельсин и ананас. Как много различных фруктовых салатов можно составить, используя только 3 фрукта? Для решения этой задачи мы можем использовать комбинаторику. В данном случае, нам нужно выбрать 3 фрукта из 5, и для этого применяется комбинация без повторений. Используя соответствующую формулу комбинации без повторений, мы можем определить, что возможно составить 10 различных фруктовых салатов.
Что такое комбинаторика в математике

Комбинаторика в математике имеет широкое применение и находит свое применение в различных областях, таких как теория вероятностей, теория кодирования, криптография и компьютерная наука.
Комбинаторика рассматривает проблемы, связанные с подсчетом и перечислением объектов. Например, сколько существует различных способов составить команду из 5 человек из группы из 10 человек? Или сколько существует различных способов распределить 10 книг на 3 полки?
В комбинаторике используются различные методы и подходы, такие как правило произведения, правило суммы, принцип Дирихле и принцип включения-исключения. Они позволяют решать сложные комбинаторные задачи и находить числовые ответы.
Комбинаторика является важной и интересной областью математики, которая находит применение во многих практических ситуациях. Понимание комбинаторики помогает лучше решать задачи подсчета и классификации и является основой для более сложных математических теорий.
Видео по теме:
Основные понятия комбинаторики

В комбинаторике используются такие основные понятия, как перестановки, сочетания и размещения:
- Перестановки — это упорядоченные наборы элементов. Например, для трех элементов A, B и C существуют 6 возможных перестановок: ABC, ACB, BAC, BCA, CAB, CBA.
- Сочетания — это неупорядоченные наборы элементов. Например, для трех элементов A, B и C существуют 3 возможных сочетания из двух элементов: AB, AC, BC.
- Размещения — это упорядоченные наборы элементов, в которых каждый элемент может использоваться только один раз. Например, для трех элементов A, B и C существуют 6 возможных размещений из двух элементов: AB, AC, BA, BC, CA, CB.
Эти понятия комбинаторики используются для решения различных задач, например, для подсчета количества возможных комбинаций лотерейных билетов, составления расписания занятий или определения вероятности определенного события.
Примеры комбинаторных задач

- Перестановки: сколькими способами можно расставить 5 книг на полке?
- Сочетания: сколькими способами можно выбрать 3 студента из группы из 10 человек?
- Размещения: сколькими способами можно выбрать 2 человека из группы из 5 человек и расположить их по порядку?
- Перегородки и шарики: сколькими способами можно разместить 3 шарика между 4 перегородками?
- Правило умножения: если у нас есть 2 независимых события, которые могут произойти соответственно в 3 и 4 случаях, то сколько всего возможных исходов?
- Задача о шахматном коне: сколько различных путей может пройти шахматный конь с одной клетки на другую?
Это только небольшая часть комбинаторных задач, которые могут возникнуть в математике, информатике, экономике и других областях. Комбинаторика играет важную роль в решении задач, связанных с подсчетом и анализом комбинаторных объектов.
Вопрос-ответ:
Что такое комбинаторика?
Комбинаторика — это раздел математики, изучающий методы счета и анализа комбинаторных структур. Она занимается решением задач на подсчет числа комбинаций, перестановок, разбиений и других комбинаторных объектов.
Какие примеры комбинаторных задач можно привести?
Примеры комбинаторных задач многочисленны. Одним из них может быть задача о количестве способов выбрать команду из группы людей, или задача о количестве способов разместить шары в ящике. Другой пример — задача о количестве путей на доске шахматного поля. Все эти задачи связаны с комбинаторикой и требуют применения комбинаторных методов для их решения.
Какие методы используются в комбинаторике?
В комбинаторике используются различные методы подсчета и анализа комбинаторных структур. Некоторые из них включают применение комбинаторных формул, рекуррентных соотношений, принципов умножения и сложения, а также использование алгоритмов перебора и генерации комбинаторных объектов.
Зачем нужна комбинаторика в математике?
Комбинаторика имеет широкое применение в различных областях науки и техники. Она позволяет решать задачи на подсчет комбинаций и вероятностные задачи, а также использовать комбинаторные методы для анализа и оптимизации процессов. Комбинаторика также является важным инструментом в криптографии, компьютерной науке и других областях, где требуется работа с комбинаторными структурами.
Перестановки

Перестановкой набора элементов называется любая упорядоченная последовательность этих элементов. Например, для набора {1, 2, 3} возможны следующие перестановки: {1, 2, 3}, {1, 3, 2}, {2, 1, 3}, {2, 3, 1}, {3, 1, 2}, {3, 2, 1}. Всего существует 3! = 6 перестановок для данного набора, где ! обозначает факториал.
Общая формула для вычисления числа перестановок n элементов равна n! = n * (n-1) * (n-2) * … * 2 * 1. Таким образом, для набора из n элементов существует n! возможных перестановок.
Перестановки широко применяются в комбинаторике, математике, программировании и других областях. Они помогают решать задачи, связанные с размещением элементов в определенном порядке и определением количества всех возможных вариантов.
Сочетания
Сочетания обычно обозначаются символом C. Например, Cnk — это количество способов выбрать из множества из n элементов k элементов без учета порядка.
Для вычисления числа сочетаний используется формула: Cnk = n! / (k! * (n — k)!), где n! — это факториал числа n.
Например, если есть множество из 5 элементов, то количество способов выбрать 3 элемента равно C53 = 5! / (3! * (5 — 3)!) = 10.
Сочетания используются в различных задачах, например, при решении задач комбинаторного анализа, теории вероятностей, а также в других областях математики и науки в целом.
Размещения

В комбинаторике термин «размещения» относится к упорядоченным выборкам элементов из заданного множества. Размещение состоит из нескольких элементов, где каждый элемент может быть выбран только один раз и порядок выбора имеет значение.
Для вычисления количества размещений, используется формула:
Ank = n! / (n — k)!
Где Ank обозначает количество размещений из n элементов по k элементов, а n! означает факториал числа n.
Например, на парковой площадке есть 5 скамеек, и мы должны выбрать 3 из них для размещения группы людей. В этом случае число размещений будет равно:
A53 = 5! / (5 — 3)! = 5! / 2! = 5 * 4 * 3 = 60
Таким образом, существует 60 различных способов разместить группу людей на 5 скамейках.
Применение комбинаторики в реальной жизни

Комбинаторика, как раздел математики, имеет широкое применение в различных сферах реальной жизни. Ее методы и принципы используются для решения задач в областях, таких как логистика, экономика, информационные технологии, генетика и другие.
Рассмотрим несколько примеров, где комбинаторика находит свое применение:
- Логистика: Комбинаторика позволяет оптимизировать распределение грузов и планирование маршрутов. Например, при планировании доставки в несколько городов, комбинаторика помогает оптимально выбрать порядок доставки грузов, учитывая различные возможные комбинации.
- Экономика: В экономике комбинаторика используется для принятия решений о размещении рекламы или оптимизации производства. Например, комбинаторные алгоритмы могут помочь определить оптимальное размещение рекламных площадей или составить оптимальный график производства, учитывая различные комбинации факторов.
- Информационные технологии: В области информационных технологий комбинаторика используется для решения задач в области безопасности данных, оптимизации поиска и других областей. Например, комбинаторные алгоритмы могут помочь обнаружить возможные комбинации паролей, упростить поиск информации или оптимизировать работу алгоритмов машинного обучения.
- Генетика: В генетике комбинаторика используется для анализа генетической информации и прогнозирования наследственных свойств. Например, комбинаторные методы могут помочь найти все возможные комбинации генов, определить вероятность наследования определенной характеристики или прогнозировать результаты генетических экспериментов.
Это лишь несколько примеров применения комбинаторики в реальной жизни. Ее методы и принципы имеют широкий спектр применения и позволяют решать разнообразные задачи во многих областях науки и промышленности.

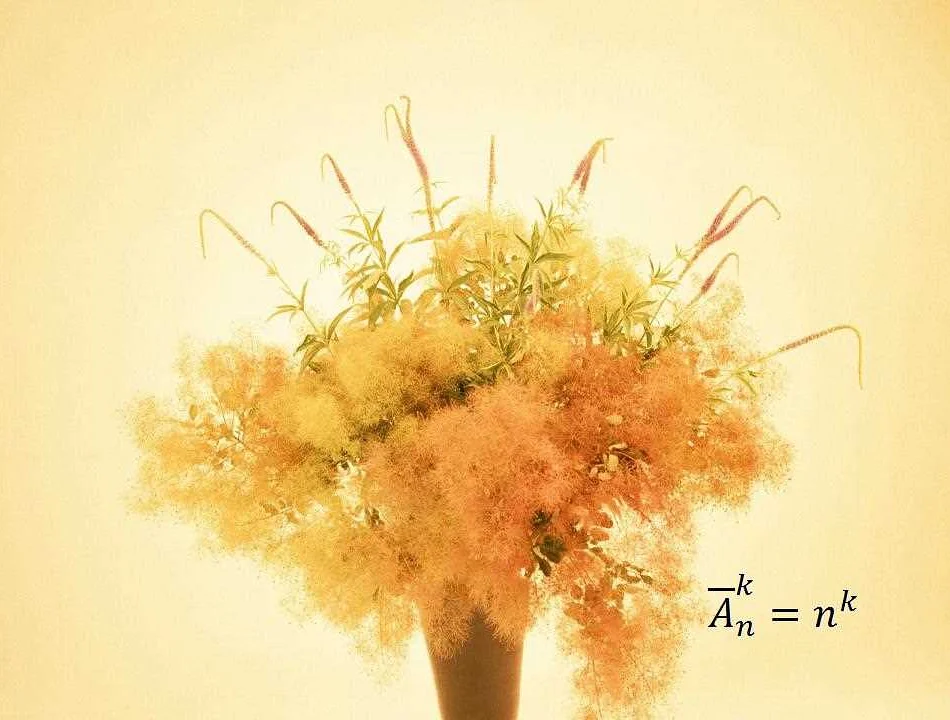



Статья прекрасно объясняет, что такое комбинаторика в математике. Мне было интересно узнать, что комбинаторика — это наука о количественном анализе различных вариантов комбинаций и перестановок. Примеры с рассчетом количества возможных комбинаций в разных ситуациях помогли мне лучше понять тему. Я теперь понимаю, что комбинаторика находит применение в разных областях, например, в теории вероятности и криптографии. Обязательно буду изучать эту тему дальше!
Очень интересная статья! Я всегда задавалась вопросом, что такое комбинаторика в математике. Спасибо автору за то, что объяснил эту сложную тему простыми словами и примерами. Теперь я лучше понимаю, каким образом можно решать задачи, связанные с расчетом вероятностей, комбинаций и перестановок. Особенно мне запомнилась идея с различными раскрасками домино. Оказывается, комбинаторика может применяться не только в математике, но и в повседневной жизни. Теперь я смогу использовать эти знания для решения сложных задач и просто для развлечения. Очень рекомендую всем прочитать эту статью и расширить свой кругозор!
Великолепная статья! Я всегда интересовался математикой, но комбинаторика была для меня настоящей загадкой до сих пор. Благодаря этой статье, я наконец-то понял, что это такое. Комбинаторика — наука о подсчете количества возможных вариантов комбинаций и перестановок. Автор прекрасно объяснил основные понятия, такие как факториал и сочетание. Очень понравились примеры, которые помогли мне лучше понять тему. Теперь я понимаю, как применять комбинаторику в повседневной жизни, например, при подсчете количества возможных вариантов одежды или меню. Спасибо автору за простые и понятные объяснения! Я уже не теряюсь в комбинаторных задачах и готов решать их с уверенностью. Очень рекомендую всем, кто хочет разобраться в комбинаторике.