Что такое перестановки в математике
Содержимое
- 1 Что такое перестановки в математике
- 1.1 Что такое перестановки в математике?
- 1.2 Видео по теме:
- 1.3 Определение понятия перестановки
- 1.4 Примеры перестановок
- 1.5 Свойства перестановок
- 1.6 Как вычислить количество перестановок?
- 1.7 Формула для вычисления числа перестановок
- 1.8 Вычисление числа перестановок с повторениями
- 1.9 Применение перестановок в математике
- 1.10 Перестановки в комбинаторике
- 1.11 Перестановки в алгебре
- 1.12 Вопрос-ответ:
- 1.12.0.1 Что такое перестановка в математике?
- 1.12.0.2 Как можно задать перестановку?
- 1.12.0.3 Каковы свойства перестановок?
- 1.12.0.4 Какие есть примеры перестановок?
- 1.12.0.5 Для чего используются перестановки в математике?
- 1.12.0.6 Что такое перестановки в математике?
- 1.12.0.7 Какие свойства имеют перестановки?
Перестановка в математике — это упорядоченный набор элементов, в котором каждый элемент встречается только один раз. Узнайте, как использовать перестановки для решения задач комбинаторики и анализа данных.
Перестановки являются одним из важных понятий в математике. В общем смысле, перестановка — это упорядоченный набор элементов, в котором каждый элемент принадлежит множеству и не повторяется. Такие наборы широко используются в различных областях математики, таких как комбинаторика, алгебра и теория вероятностей.
Для определения перестановок удобно использовать понятие факториала. Факториал числа n (обозначается n!) — это произведение всех натуральных чисел от 1 до n включительно. Например, факториал числа 5 равен 5! = 5 * 4 * 3 * 2 * 1 = 120. Число перестановок множества из n элементов равно n!.
Пример: Пусть у нас есть множество из трех элементов: A = {1, 2, 3}. В данном случае мы можем составить 3! = 3 * 2 * 1 = 6 различных перестановок: {1, 2, 3}, {1, 3, 2}, {2, 1, 3}, {2, 3, 1}, {3, 1, 2}, {3, 2, 1}.
Перестановки обладают рядом интересных свойств. Например, количество перестановок множества из n элементов равно n!. Также можно заметить, что количество перестановок, в которых два элемента остаются на своих местах, равно (n-2)!. Это свойство называется инверсией перестановки. Кроме того, перестановки могут быть коммутативными или некоммутативными, в зависимости от того, сохраняется ли порядок элементов при их перестановке.
Изучение перестановок имеет важное значение для решения задач комбинаторики, а также для понимания основных принципов и свойств линейной алгебры и теории вероятностей. Знание основных определений, примеров и свойств перестановок позволяет более глубоко понять и применять математические концепции в различных областях науки и техники.
Что такое перестановки в математике?
Формально, перестановка — это упорядоченная последовательность элементов множества. Другими словами, это способ упорядочить элементы множества так, чтобы каждый элемент присутствовал ровно один раз.
Перестановки являются важными в математике и имеют разнообразные применения. Они используются в теории вероятностей, комбинаторике, алгебре, криптографии и других областях. Понимание перестановок помогает решать задачи, связанные с упорядочиванием элементов и нахождением числа возможных комбинаций.
Существует несколько способов представления перестановок математически. Один из них — использование индексов для обозначения порядка элементов. Например, перестановка (1, 2, 3) обозначает, что первым элементом является 1, вторым — 2, и третьим — 3.
Число перестановок зависит от количества элементов, которые нужно переставить. Для множества из n элементов, число перестановок равно n!. Вертикальная черта, обозначающая факториал, означает произведение всех натуральных чисел от 1 до n. Например, для множества из 3 элементов существует 3! = 3 * 2 * 1 = 6 перестановок.
Перестановки могут быть рассмотрены как особый случай комбинаций, где учитывается порядок элементов. Они также могут быть использованы для решения задач распределения объектов или задач, связанных с размещением элементов в различных вариантах.
Видео по теме:
Определение понятия перестановки

Перестановка задается списком элементов, которые могут быть переупорядочены. Например, для множества {1, 2, 3} возможны следующие перестановки: (1, 2, 3), (1, 3, 2), (2, 1, 3), (2, 3, 1), (3, 1, 2), (3, 2, 1).
Перестановки играют важную роль в комбинаторике, так как они позволяют рассматривать различные упорядоченные состояния элементов множества. Они также используются в алгебре для изучения групп и в теории вероятностей для расчета различных комбинаций и вероятностей событий.
Примеры перестановок

Перестановкой называется любое упорядочивание элементов некоторого множества. Рассмотрим несколько примеров перестановок:
1. Множество {1, 2, 3} имеет 6 перестановок: {1, 2, 3}, {1, 3, 2}, {2, 1, 3}, {2, 3, 1}, {3, 1, 2}, {3, 2, 1}.
2. Множество {a, b, c, d} имеет 24 перестановки.
3. Множество {x, y, z} имеет также 6 перестановок: {x, y, z}, {x, z, y}, {y, x, z}, {y, z, x}, {z, x, y}, {z, y, x}.
4. Множество {a, b, c} имеет 6 перестановок: {a, b, c}, {a, c, b}, {b, a, c}, {b, c, a}, {c, a, b}, {c, b, a}.
5. Множество {p, q} имеет 2 перестановки: {p, q}, {q, p}.
Таким образом, количество перестановок зависит от количества элементов в исходном множестве и рассчитывается по формуле n!, где n — количество элементов.
Свойства перестановок
Свойства перестановок:
- Каждая перестановка состоит из всех элементов множества, причем каждый элемент встречается ровно один раз.
- Количество перестановок из n элементов равно n! (факториал n).
- Перестановки можно умножать друг на друга. Результатом умножения перестановок является композиция перестановок.
- Умножение перестановок не коммутативно. То есть, результат умножения перестановок A и B может быть разным, в зависимости от порядка умножения (AB ≠ BA).
- Каждая перестановка имеет обратную перестановку. Обратная перестановка получается путем обращения порядка элементов в исходной перестановке.
- Перестановки можно разбить на транспозиции, которые меняют местами два элемента. Любая перестановка может быть представлена как композиция транспозиций.
Свойства перестановок позволяют решать различные задачи в математике и других областях, таких как теория графов, теория вероятностей и криптография.
Как вычислить количество перестановок?
Чтобы вычислить количество перестановок, необходимо знать количество объектов, которые нужно переставить, и количество доступных позиций для каждого объекта. В общем случае, количество перестановок равно произведению факториалов чисел, соответствующих количеству объектов и позиций.
Например, пусть у нас есть 3 объекта и 3 доступные позиции для каждого из них. Чтобы найти количество перестановок, нужно вычислить факториал числа 3 и умножить его на само себя 3 раза. Факториал 3 равен 3! = 3 * 2 * 1 = 6, поэтому количество перестановок будет равно 6 * 6 * 6 = 216.
Для удобства и более сложных случаев, когда количество объектов и позиций больше, можно использовать таблицу для вычисления количества перестановок. В таблице указывается количество объектов в первом столбце и количество доступных позиций в первой строке. Затем, пересечение строки и столбца даёт количество перестановок для соответствующих значений.
| 1 | 2 | 3 | |
| 1 | 1 | 1 | 1 |
| 2 | 2 | 4 | 8 |
| 3 | 6 | 12 | 24 |
Например, в таблице выше пересечение строки 2 и столбца 3 дает значение 8, что означает, что при 2 объектах и 3 доступных позициях есть 8 возможных перестановок. Таким образом, таблица помогает быстро и легко определить количество перестановок для различных значений.
Формула для вычисления числа перестановок
Число перестановок элементов множества можно вычислить с помощью формулы для перестановок без повторений:
P(n) = n!
где P(n) — число перестановок, n — количество элементов в множестве, и «!» обозначает факториал числа.
Факториал числа n равен произведению всех положительных целых чисел, меньших или равных n.
Например, для множества из 4 элементов (n = 4) количество перестановок будет:
P(4) = 4! = 4 * 3 * 2 * 1 = 24
Таким образом, существует 24 различных перестановки элементов в данном множестве.
Вычисление числа перестановок с повторениями

Число перестановок с повторениями определяется как количество различных способов переставить элементы множества, в котором имеются повторяющиеся элементы.
Для вычисления числа перестановок с повторениями необходимо учитывать, сколько раз каждый элемент повторяется в множестве. Если имеется n элементов, из которых k1 повторяются один раз, k2 повторяются два раза и т.д., то общее число перестановок с повторениями можно найти по формуле:
n! / (k1! * k2! * … * kn!)
где n — общее количество элементов, ki — количество повторяющихся элементов i-го типа.
Например, если имеется множество {A, A, B, C, C, C}, то общее число перестановок с повторениями будет:
6! / (2! * 1! * 3!) = 60
Таким образом, существует 60 различных способов переставить элементы данного множества.
Применение перестановок в математике
Перестановки играют важную роль в различных областях математики. Они широко применяются в комбинаторике, алгебре, теории вероятностей и других математических дисциплинах.
В комбинаторике перестановки используются для решения задач на расположение объектов в определенном порядке. Например, перестановки могут помочь определить количество способов упорядочить элементы в последовательности или выбрать комитет из набора кандидатов.
В алгебре перестановки являются основным инструментом для изучения симметрий и групп. Группа перестановок, также известная как симметрическая группа, состоит из всех возможных перестановок некоторого конечного множества. Симметрические группы имеют множество интересных свойств и являются объектом исследования в алгебре.
В теории вероятностей перестановки используются для вычисления количества исходов в экспериментах с различными перестановками объектов. Например, перестановки могут быть использованы для определения вероятности получения определенной комбинации карт в игре.
Таким образом, перестановки являются мощным инструментом, который позволяет решать задачи в различных областях математики. Их применение не ограничивается только комбинаторикой, а также распространено в алгебре и теории вероятностей.
Перестановки в комбинаторике

Количество возможных перестановок зависит от количества элементов, которые нужно переставить. Для набора из n элементов, число перестановок обозначается как n!, где «!» обозначает факториал. Факториал — это произведение всех натуральных чисел от 1 до n.
Например, если у нас есть набор из 3 элементов, то количество возможных перестановок будет 3! = 3 * 2 * 1 = 6. Эти перестановки могут быть представлены следующим образом: ABC, ACB, BAC, BCA, CAB, CBA.
Перестановки в комбинаторике широко применяются для решения различных задач. Например, они используются при решении задач о рассадке гостей за столом, распределении призов между участниками конкурса и т.д.
Одной из важных особенностей перестановок является то, что порядок элементов имеет значение. Другими словами, перестановки ABC и BAC считаются разными, поскольку элементы расположены в разном порядке.
Также стоит отметить, что перестановки могут быть с повторениями. В этом случае, некоторые элементы могут повторяться, и количество возможных перестановок будет меняться.
Выводящий блок: Перестановки в комбинаторике — это упорядоченные последовательности элементов, в которых каждый элемент встречается ровно один раз. Они используются для решения различных задач, и количество возможных перестановок зависит от количества элементов и возможности повторения.
Перестановки в алгебре

Пусть у нас имеется множество, состоящее из n элементов. Перестановкой этого множества называется упорядоченная последовательность всех его элементов. Обозначается перестановка символом σ.
Перестановки могут быть записаны в виде таблицы или в виде циклов.
Таблица перестановки представляет собой строку, в которой каждому элементу множества соответствует другой элемент. В таблице перестановки перестановка представлена в виде набора пар {i,σ(i)}, где i — элемент множества, а σ(i) — соответствующий ему элемент перестановки.
Цикловая запись перестановки представляет собой последовательность элементов, таких, что каждый элемент заменяется следующим элементом в цикле, а последний элемент заменяется первым. Например, перестановку (1 2 3 4) можно записать в виде цикла (1 2 3 4).
Перестановки в алгебре обладают рядом важных свойств и операций. Например, можно выполнять сложение, вычитание и умножение перестановок. Также можно находить обратную перестановку, находить количество инверсий в перестановке и многое другое.
Перестановки в алгебре имеют широкое применение в теории групп, теории алгебраических систем, комбинаторике и других областях математики.
Вопрос-ответ:
Что такое перестановка в математике?
Перестановка — это упорядоченная последовательность элементов, полученная из исходной последовательности путем изменения порядка элементов.
Как можно задать перестановку?
Перестановку можно задать двумя способами: в виде упорядоченного списка элементов или в виде циклов.
Каковы свойства перестановок?
Перестановки обладают следующими свойствами: каждый элемент исходной последовательности участвует в перестановке ровно один раз, у перестановки есть обратная перестановка, композиция перестановок ассоциативна.
Какие есть примеры перестановок?
Примеры перестановок включают перестановки чисел от 1 до n, перестановки букв в словах или предложениях, перестановки карт в колоде и т. д.
Для чего используются перестановки в математике?
Перестановки широко используются в комбинаторике, теории вероятностей, алгебре, криптографии и других областях математики. Они помогают решать задачи на подсчет количества различных упорядоченных объектов и разработке алгоритмов.
Что такое перестановки в математике?
Перестановками в математике называются упорядоченные наборы элементов, получаемые путем изменения порядка элементов в исходном наборе.
Какие свойства имеют перестановки?
Перестановки обладают несколькими свойствами, включая ассоциативность, коммутативность и наличие обратной перестановки. Ассоциативность означает, что результат последовательной композиции двух перестановок не зависит от порядка их выполнения. Коммутативность означает, что результат композиции двух перестановок не зависит от их порядка. Наличие обратной перестановки означает, что каждая перестановка имеет обратную, которая отменяет эффект данной перестановки.


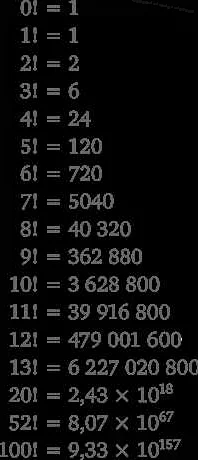
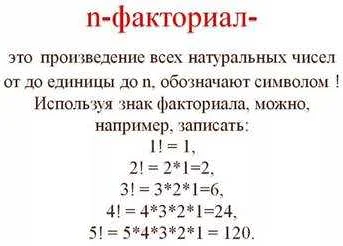
Отличная статья! Я всегда была заинтригована перестановками в математике, но никогда не совсем понимала их суть. Теперь все стало ясно благодаря вашему объяснению. Я была поражена тем, как множество чисел можно переставлять и получать разные результаты. Это действительно удивительно и захватывающе! Особенно интересно было узнать о свойствах перестановок и то, что они могут быть представлены в виде циклов. Теперь мне хочется попробовать создать свои собственные перестановки и посмотреть, что из этого получится. Спасибо за замечательную статью, которая открыла мне новый мир математики!
Интересная статья! Я всегда была увлечена математикой, и перестановки — одна из самых захватывающих и важных тем в этой науке. Определение перестановок, приведенное в статье, просто и понятно объясняет, что это упорядоченные изменения порядка элементов. Примеры перестановок, такие как перестановки набора чисел или букв, иллюстрируют, как они могут быть использованы на практике. Интересно узнать о свойствах перестановок, таких как коммутативность и ассоциативность. Это позволяет нам лучше понять и использовать их в решении различных задач. Статья дает хорошую базу и знания для дальнейшего изучения перестановок. Буду продолжать читать о математике и ее приложениях!
Статья очень понравилась! Я всегда была заинтригована темой перестановок в математике. Отличные примеры и подробные объяснения помогли мне лучше понять эту концепцию. Я была удивлена узнать, что перестановки могут применяться в таких различных областях, как комбинаторика, криптография и даже в музыке! Также интересно узнать, что есть такое понятие, как перестановка с повторениями. Я с нетерпением жду возможности попробовать решить некоторые задачи на перестановки самостоятельно. Большое спасибо за статью и за то, что делаете математику более доступной и увлекательной!