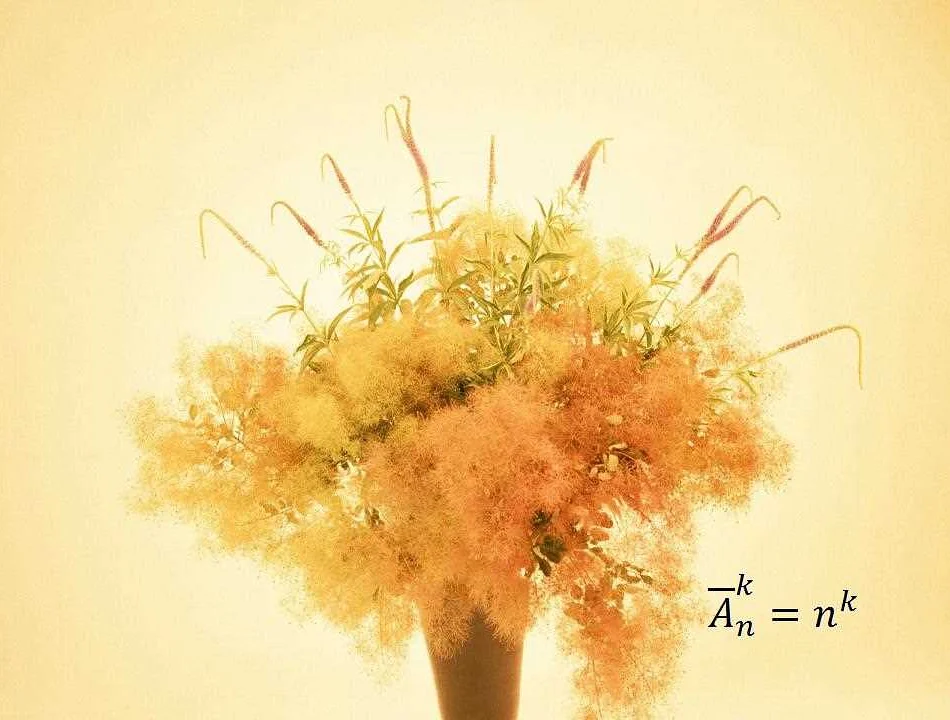Комбинаторика: изучаем количество различных сочетаний в математике

Изучаем комбинаторику — область математики, где рассматриваются вопросы количества возможных комбинаций. Узнайте, как вычислять количество комбинаций и применять их в решении конкретных задач.

Комбинаторика – это раздел математики, который изучает количество комбинаций и перестановок элементов в заданном множестве. Эта наука нашла применение в различных областях жизни – от управления логистикой до обработки данных в компьютерных науках.

Изучение комбинаторики является важной частью обучения математике, которая развивает умение находить и анализировать решения задач с учетом возможных комбинаций. При изучении этой науки, студенты учатся эффективно решать задачи, используя логическое мышление и математический анализ.

В этой статье мы рассмотрим основные концепции комбинаторики и примеры их применения. Вы узнаете, как работать с сочетаниями и перестановками, как определить количество комбинаций и многое другое. Приготовьтесь узнать новое и захватывающее поле математики!

Что такое комбинаторика?

Комбинаторика — это раздел математики, изучающий сочетания и перестановки. Она помогает решать задачи, связанные с выбором объектов из некоторого множества и их расположением в определенном порядке.

Комбинаторика находит применение в различных областях, включая теорию вероятностей, комбинаторную геометрию, теорию кодирования и прочие. Она используется для решения задач, связанных с выбором представителей, распределением ресурсов и многих других.

Изучение комбинаторики позволяет не только решать разнообразные задачи, но и развивать логическое мышление, аналитические способности и математическую интуицию.

Основные понятия комбинаторики — это перестановки и сочетания. Перестановки — это способы расположения объектов в определенном порядке. Сочетания — это способы выбора объектов без учета их порядка.

В комбинаторике используются различные методы решения, включая перебор, комбинаторный анализ и принцип Дирихле. Каждый из этих методов имеет свои преимущества и может быть применен в зависимости от конкретной задачи.

Одной из особенностей комбинаторики является ее широкое применение в решении повседневных задач. Например, комбинаторика может использоваться для подсчета количества возможных сочетаний товаров в магазине, комбинаций расстановки сотрудников на рабочих местах и прочих задач, связанных с выбором и распределением объектов.

Таким образом, комбинаторика — это важный раздел математики, который помогает решать реальные задачи и развивать мышление. Изучение комбинаторики имеет множество практических применений и может быть очень полезным для людей, работающих в различных сферах жизни.

Что такое сочетания и перестановки?

Сочетания и перестановки — это два понятия из области комбинаторики. Комбинаторика занимается изучением количественных соотношений из элементов, составляющих заданное множество.

Перестановки — это количество способов расположения элементов в некотором порядке. Например, для элементов A, B, C наиболее известные перестановки — ABC, ACB, BAC, BCA, CAB, CBA. Общая формула для количества перестановок из n элементов равна n!.

Сочетания — это количество различных комбинаций элементов, которые можно получить из данного множества, но без учета порядка. Например, для элементов A, B, C сочетаниями без повторений являются: AB, AC, BC. Общая формула для количества сочетаний без повторений из n элементов по k элементов равна С(n, k) = n!/k!(n-k)!.

Знание комбинаторики полезно не только для изучения математики, но также находит применение в различных областях науки и ежедневной жизни, например, при составлении расписания, распределении ресурсов, и т.д.

Формулы для нахождения количества комбинаций и перестановок

В комбинаторике для нахождения количества комбинаций можно использовать формулу C(n, k), где n — это количество элементов в множестве, а k — количество элементов в подмножестве. Формула записывается следующим образом:

C(n, k) = n!/k!(n-k)!

Данная формула позволяет расчитать комбинации без учета порядка элементов в подмножестве.

Формула для нахождения перестановок включает в себя количество способов переставить элементы множества в разных порядках. Формула для нахождения количества перестановок записывается как P(n), где n — количество элементов в множестве, и выглядит следующим образом:

P(n) = n!

Например, для множества из четырех элементов (a, b, c, d) существует 24 перестановки:

• abcd
• abdc
• acbd
• acdb
• adbc
• adcb
• …

Таким образом, знание формул для нахождения количества комбинаций и перестановок позволяет решать задачи, связанные с выборкой и расположением элементов в множестве.

Примеры решения задач на комбинаторику

Комбинаторика – это раздел математики, который изучает комбинации и перестановки объектов. Задачи на комбинаторику могут быть очень разнообразными и интересными. Рассмотрим несколько примеров.

Пример 1. В книжном магазине есть 5 разных книг по математике и 3 разные книги по физике. Сколькими способами можно выбрать 4 книги для покупки?

В данной задаче нужно выбрать 4 книги из 8. Это можно сделать сочетанием из 8 по 4:

℘(8,4)

=

8

7

6

5

/

4

3

2

1

= 70

Ответ: можно выбрать 4 книги на 70 способов.

Пример 2. В школе учится 20 человек. Сколькими способами можно выбрать команду из 5 учеников?

В данной задаче нужно выбрать 5 человек из 20. Это можно сделать сочетанием из 20 по 5:

℘(20,5)

=

20

19

18

17

16

/

5

4

3

2

1

= 15504

Ответ: можно выбрать команду из 5 учеников на 15504 способа.

Пример 3. В классе 10 учеников. Сколькими способами можно выбрать команду капитанов и заместителей, если капитанов нужно выбрать 2, а заместителей 3?

Эту задачу можно решить с помощью перестановок. Сначала нужно выбрать 2 капитанов из 10, это можно сделать сочетанием из 10 по 2. Затем нужно выбрать 3 заместителей из 8 оставшихся учеников, это можно сделать сочетанием из 8 по 3. Итого получаем, что команду можно выбрать:

№(10,2)№(8,3)

= 45·56 = 2520

Ответ: команду капитанов и заместителей можно выбрать на 2520 способов.

Задачи повышенной сложности на комбинаторику

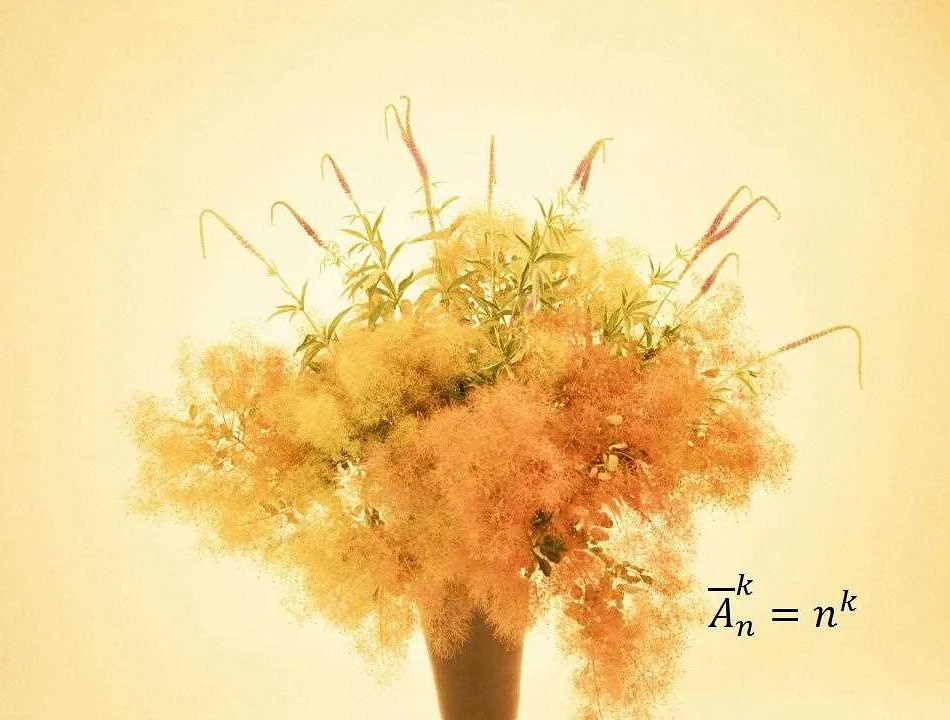
В комбинаторике простых задач не бывает, но существуют и более сложные, требующие особого внимания. Ниже представлены несколько примеров задач повышенной сложности на комбинаторику.

Задача о расстановке шаров в ящиках

Имеются 10 различных шаров и три различных ящика. Сколькими способами можно расставить эти шары в ящиках?

Для решения этой задачи необходимо использовать теорию комбинаторных объектов. Нужно выяснить, сколько различных комбинаций числа шаров в каждом ящике возможно при заданных условиях. Расстановка происходит следующим образом: в каждый ящик можно поместить от 0 до 10 шаров, при этом число шаров в ящике может быть одинаковым или различным от других ящиков.

Задача о перестановках

Сколько различных перестановок можно составить из букв слова «картина»?

Для решения данной задачи следует использовать формулу перестановки. Перестановка — это упорядоченное размещение элементов множества. Для слова «картина» можно составить 7! (5040) различных перестановок.

Задача о сочетаниях

Сколькими способами можно выбрать 3 предмета из 8?

Для решения данной задачи нужно применить формулу сочетания. Сочетание — это неупорядоченный набор элементов из множества. Для выбора 3 предметов из 8 необходимо применить формулу сочетания: C(8,3) = 56. То есть, всего 56 сочетаний.

Таким образом, комбинаторика представляет собой область математики, которая может быть применена в различных сферах, начиная от составления расписания, заканчивая разработкой сложных алгоритмов. При этом, задачи повышенной сложности на комбинаторику требуют обширных знаний и навыков в области математического анализа и логической мысли.

Как применять знания комбинаторики в повседневной жизни?

Комбинаторика — это мощный инструмент для решения задач, связанных с количеством возможных вариантов различных выборов и расположений. Знания комбинаторики могут помочь в повседневной жизни во многих областях, например:

1. Планирование маршрута: при планировании поездок или путешествий нужно выбрать оптимальный маршрут, учитывая все возможные варианты путей и сочетаний мест, которые хотите посетить. Некоторые задачи могут быть решены с помощью перестановок и сочетаний.
2. Конструирование: при выборе цветов и материалов для дома, сада или гардероба вы можете использовать знания комбинаторики для создания гармоничных сочетаний. Например, можно определить число возможных цветовых комбинаций и составить таблицу для сравнения.
3. Бизнес и финансы: при принятии решений в бизнесе и финансах могут быть очень полезны знания комбинаторики. Например, при планировании рекламной кампании нужно рассчитать количество возможных сочетаний объявлений и каналов распространения, а при анализе инвестиционных возможностей — количество вариантов распределения активов.
4. Игры: знания комбинаторики могут помочь при игре в шахматы, покер или другие игры, где важны возможные сочетания и перестановки фигур или карт. Например, можно определить число возможных ходов или комбинаций карт и использовать эту информацию при принятии решений.

Таким образом, знания комбинаторики могут быть полезны практически везде, где нужно делать выбор из множества возможностей и определять количество вариантов. При этом важно не зацикливаться на теории, а уметь применять знания комбинаторики в конкретных ситуациях, рассматривая каждый случай отдельно.

История развития комбинаторики как науки

Комбинаторика — область математики, изучающая перестановки, сочетания и размещения объектов. Развитие комбинаторики началось в Древней Греции, где ее занимались ученые, такие как Эвдокс, Аристотель и Евклид.

Однако, настоящей золотой эрой для комбинаторики стал 17-й век, когда знаменитый французский математик Блез Паскаль стал изучать задачи комбинаторного типа. Вместе с Рене Декартом они создали теорию вероятности, что существенно повлияло на развитие комбинаторики.

19-й век стал временем активного развития комбинаторики. Одним из ее великих представителей был польский математик Владислав Шимановский, который занимался свойствами размещений, комбинаций и перестановок. Еще одним выдающимся ученым этого времени был Готфрид Лейбниц, который разработал теорию булевых функций.

В 20-й век комбинаторика получила толчок к активному развитию, благодаря развитию электронной вычислительной техники. Появились новые алгоритмы и методы решения комбинаторных задач, а также идеи, которые ранее были невообразимыми, такие как квантовая комбинаторика.

На сегодняшний день комбинаторика является важной областью математики и науки, с широким применением в информатике, экономике, физике, биологии и других областях знаний.

Перспективы развития комбинаторики в будущем

Комбинаторика – область математики, которая изучает сочетания и перестановки. Сегодня она находится в стадии активного развития и имеет широкие перспективы в будущем. Ее применение распространяется на многие науки, включая физику, информатику, экономику и другие.

В будущем комбинаторика будет развиваться в направлении обработки больших объемов информации. Сейчас ученые разрабатывают новые методы и алгоритмы решения задач, которые помогут обрабатывать и анализировать огромные массивы данных.

Кроме того, комбинаторика имеет широкие применения в криптографии. Ученые разрабатывают новые методы шифрования и дешифровки данных, используя сочетания и перестановки. Это значительно улучшает защиту информации и позволяет защитить ее от несанкционированного доступа.

Еще одной перспективой развития комбинаторики является ее применение в стратегическом планировании и принятии решений. Сочетания и перестановки позволяют проводить анализ данных и выстраивать эффективные стратегии развития бизнеса и других проектов.

Таким образом, развитие комбинаторики в будущем будет направлено на решение сложных задач обработки информации, криптографии и стратегического планирования.

Видео по теме:

Вопрос-ответ:

Что такое сочетания?

Сочетание — это комбинация из k элементов, выбранных из n элементов, где порядок не имеет значения. Формула для нахождения количества сочетаний C(n,k) выглядит так: C(n,k) = n! / (k! * (n-k)!).

Чем отличаются сочетания от перестановок?

Сочетания и перестановки — это два понятия комбинаторики, которые часто путают вместе. Основное отличие между ними заключается в том, что в случае сочетаний порядок элементов не имеет значения, а в случае перестановок — имеет. То есть, в сочетаниях, выборка из n элементов может принимать разные комбинации из k элементов, а в перестановках, каждая из комбинаций может быть переставлена.

Как найти количество перестановок?

Количество перестановок из n элементов вычисляется по формуле P(n) = n!, где n — количество элементов. Например, если у нас имеется 3 элемента, то количество перестановок будет равно 3! = 6.

В каких областях жизни применяется комбинаторика?

Комбинаторика применяется в различных областях жизни, таких как теория вероятностей, криптография, теория кодирования, компьютерные науки, математическая статистика, игровая теория и другие. Например, в криптографии комбинаторика используется для создания защищенных паролей, а в математической статистике — для анализа данных.

Как находить сочетания и перестановки с помощью программирования?

В языках программирования существуют готовые функции, которые позволяют находить сочетания и перестановки. Например, в Python для нахождения сочетаний можно использовать функцию itertools.combinations(), а для перестановок — itertools.permutations().

Какие есть формулы для нахождения сочетаний?

Существует несколько формул для нахождения сочетаний. Одна из них — это формула n! / (k! * (n-k)!) , где n — количество элементов, а k — количество элементов в сочетании. Еще одна формула — это формула (n k) = (n-1 k-1) + (n-1 k), где (n k) — количество сочетаний из n элементов по k.

Как доказать, что количество перестановок из n элементов равно n! ?

Для доказательства формулы, показывающей количество перестановок, можно использовать метод математической индукции. Базовый шаг — это показать, что формула верна для n=1, т.к. 1! = 1. Затем нужно показать, что если формула верна для n=k, то она верна и для n=k+1. Для этого нужно умножить n! на (k+1) и показать, что результат равен (k+1)!.

Современные достижения в области комбинаторики

Комбинаторика является одной из фундаментальных областей математики и науки в целом. Она изучает способы счета и описывает свойства математических объектов различных видов. Современные достижения в области комбинаторики объединяются в несколько ключевых областей:

• Комбинаторное проектирование — это наука, изучающая способы построения комбинаторных объектов, таких как блочные матрицы, коды, конечные графы и т.д.
• Теория перестановок — это область, связанная с изучением перестановок элементов, например при решении задач о перестановке букв в словах или чисел в числовых последовательностях.
• Теория графов — это область, изучающая свойства и структуры графов, где вершины представляют объекты, а ребра — связи между ними. Теория графов нашла широкое применение в технических науках, как например при проектировании сетей связи.

Одним из важных приложений комбинаторики является криптография. Эта область науки изучает методы шифрования информации для обеспечения безопасности передачи данных. Комбинаторика используется при создании алгоритмов шифрования и методов проверки их безопасности.

Современные достижения в области комбинаторики применяются в широком спектре областей, от компьютерных наук до генетики. Развитие этой науки способствует разработке новых технологий и способов решения сложных задач, поэтому ее изучение является актуальным и важным для научного и технического прогресса.

Знаменитые ученые-комбинаторы и их вклад в науку

Блез Паскаль — французский математик и философ, один из основоположников теории вероятностей и комбинаторики. Он разработал триангуляционную схему для решения задачи о шарах в ящиках, изучал числа Каталана и занимался проективной геометрией. Кроме того, Паскаль совместно со своими коллегами разработал первую механическую калькулятор, который стал предвестником современных компьютеров.

Готфрид Лейбниц — немецкий ученый, рассматривавший комбинаторику и логику как инструменты для нахождения истины. Он использовал булеву алгебру, чтобы выразить логические идеи и занимался созданием символических логик для анализа математических проблем в 17 веке. Лейбниц также разработал первую механическую машину для вычисления чисел, позже развившуюся в арифмометр. В качестве математика, Лейбниц служил источником вдохновения для многих следующих ученых, в том числе для Эйлера.

Леонард Эйлер был швейцарским математиком, который внес значительный вклад в комбинаторику. Он разработал ряд стратегий для решения задач комбинаторики, включая зеркальную симметрию и производящие функции. Кроме того, он занимался числовыми представлениями графов, теорией вероятностей, численными методами и многими другими областями математики.

Эрдёш Пауль — венгерский математик-комбинаторик, который известен своими работами в области теории графов, комбинаторики и теории чисел. Его теории включают понятие индексированного семейства и гипотезу Эрдёша-Коши, содержащую предположение о том, что каждое конечное множество имеет минимальное ненулевое натуральное число в качестве суммы простых чисел.

Ричард Стэнли — американский ученый, работающий в области комбинаторики, теории алгоритмов и теории групп. Он известен своей работой в области перечисления комбинаторных объектов, включая различные классы строений, такие как графы, деревья и перестановки. Стэнли также занимался теорией Фробениуса, гипотезой Рамсея и гипотезой Эйлера.