Что такое корень в математике

Корень в математике — это операция обратная возведению в степень. Корень из числа — это число, при возведении в данную степень даёт исходное число. Узнайте, как находить корень и какие существуют его свойства.

Корень – одно из важнейших понятий в математике, которое широко применяется в различных областях этой науки. Корень является обратной операцией для возведения в степень и позволяет находить такое число, при возведении в заданную степень которого получается исходное число. Например, корень квадратный из числа 9 равен 3, так как 3 в квадрате равно 9.

Корни имеют свои особенности и свойства. Например, корень из отрицательного числа невозможно найти в области действительных чисел, поэтому вводится комплексная плоскость, где операция извлечения корня из отрицательных чисел возможна. Кроме того, корень является функцией, которая обладает множеством свойств, таких как коммутативность, ассоциативность и дистрибутивность.

Примеры применения корня в математике можно приводить множество. Например, в физике корень используется для нахождения расстояния при заданной скорости и времени. В геометрии корень используется для нахождения длины стороны треугольника или радиуса окружности. В алгебре корень используется для решения квадратных уравнений и вычисления значений функций.

Всего лишь немногие свойства и применения корня в математике были упомянуты в этой статье. Однако, это понятие играет важную роль в различных областях науки и имеет множество интересных свойств и приложений.

Определение корня в математике

Математически записывается как: an = b, где a — основание корня, n — показатель степени, b — результат возведения в степень.

Например, если число 4 возвести в квадрат, то получится 16. В этом случае число 4 является корнем степени 2 из числа 16.

Видео по теме:

Что такое корень в математике?

Корень может быть выражен как приближенное значение, например, известен корень квадратный из числа 2: приближенно он равен 1,41421. А также корень может быть представлен в виде рациональной дроби или десятичной дроби.

Корень обозначается символом √. Например, корень квадратный из числа a записывается как √a.

Корень в математике имеет некоторые свойства:

• Корень из положительного числа всегда положителен.
• Корень из нуля равен нулю.
• Корень из отрицательного числа является мнимым числом и записывается с использованием символа i. Например, корень квадратный из -4 равен 2i.
• Корень из произведения равен произведению корней. Например, корень квадратный из числа 4 умноженный на корень квадратный из числа 9 равен 2 * 3 = 6.
• Корень из частного равен частному корней. Например, корень квадратный из числа 16 разделенный на корень квадратный из числа 4 равен 4 / 2 = 2.

В математике корни широко используются для решения уравнений и вычисления значений функций.

Свойства корня в математике

Свойства корня включают:

1. Свойство выделения корня: корень из произведения равен произведению корней. То есть √(а · b) = √а · √b.
2. Свойство сокращения корня: корень из частного равен частному корней. То есть √(а / b) = √а / √b.
3. Свойство взятия корня из степени: корень из числа в степени равен числу взятому в этой степени. То есть √(а^b) = а^(b/2).
4. Свойство корня из корня: корень из корня равен корню суммы показателей степеней. То есть √(√а) = а^(1/4).

Таким образом, зная эти свойства, можно упростить выражения с корнем и выполнять различные операции с корнями.

Вопрос-ответ:

Что такое корень в математике?

Корень в математике — это операция, обратная возведению в степень. Если задано число a и натуральное число n, то корнем степени n из числа a называется такое число x, что x^n = a. В математической записи это выглядит как x = √(n) a.

Какие свойства имеют корни в математике?

Корни в математике обладают несколькими важными свойствами. Во-первых, существует только одно положительное число, которое имеет заданный натуральный корень. Во-вторых, если число a положительное, то корень из него тоже положителен. В-третьих, если число a равно нулю, то корень из него тоже равен нулю. В-четвертых, если число a отрицательное и степень корня четная, то корень из него будет комплексным числом.

Как найти корень из числа?

Чтобы найти корень из числа, нужно взять заданное число и возвести его в степень, обратную степени корня. Например, чтобы найти квадратный корень из числа a, нужно найти такое число x, что x^2 = a, и извлечь из него корень. Для этого можно использовать калькулятор, таблицы квадратных корней или методы численного анализа.

Какие есть примеры корней в математике?

Примеры корней в математике могут быть разнообразными. Например, квадратный корень из числа 16 равен 4, так как 4^2 = 16. Кубический корень из числа 8 равен 2, так как 2^3 = 8. Корень четвертой степени из числа 625 равен 5, так как 5^4 = 625. И так далее. Корни могут быть как целыми числами, так и десятичными дробями, а в некоторых случаях — и комплексными числами.

Зачем нужны корни в математике?

Корни в математике имеют широкое применение в различных областях. Они позволяют решать уравнения, находить значения функций, находить длины сторон геометрических фигур и многое другое. Корни также используются для вычисления интересующих нас значений и для упрощения выражений. Они являются важным инструментом в алгебре, геометрии, физике и других науках, а также в повседневной жизни.

Что такое корень в математике?

Корень в математике — это операция обратная возведению в степень. Если число a возведено в степень n и равно b, то корень из числа b с показателем n равен числу а. Иными словами, корень из числа b — это такое число a, что a в степени n равно b.

Как найти корень из числа?

1. Методы вычисления корня из числа с использованием алгоритма Ньютона. Этот метод позволяет приближенно найти корень из числа с заданной степенью. Алгоритм Ньютона основан на построении последовательности приближений, которые сходятся к искомому корню. Для этого необходимо выбрать начальное приближение и итерационно уточнять его.

2. Методы вычисления корня из числа с использованием разложения в ряд. Один из таких методов — метод Биномиального расширения. Он основан на разложении биномиальной формулы в ряд Тейлора. Данный метод позволяет приближенно вычислить корень из числа, используя конечное количество членов ряда.

3. Использование таблицы квадратных корней. Для вычисления квадратных корней часто используется таблица, в которой указаны значения корней для различных чисел. По заданному числу можно найти соответствующий ему корень в этой таблице.

4. Использование калькулятора. Для нахождения корня из числа с заданной степенью можно воспользоваться калькулятором, который имеет специальную функцию для вычисления корней. На калькуляторе необходимо ввести число и указать степень корня, после чего будет получено значение корня.

Таким образом, для нахождения корня из числа существуют различные методы, которые позволяют приближенно или точно вычислить значение корня. Выбор метода зависит от требуемой точности и доступных инструментов вычисления.

Примеры корней в математике

1. Квадратный корень из числа 16 равен 4, так как 4 * 4 = 16.

2. Кубический корень из числа 27 равен 3, так как 3 * 3 * 3 = 27.

3. Корень четвертой степени из числа 16 равен 2, так как 2 * 2 * 2 * 2 = 16.

4. Корень пятой степени из числа 243 равен 3, так как 3 * 3 * 3 * 3 * 3 = 243.

5. Корень десятой степени из числа 1024 равен 2, так как 2 * 2 * 2 * 2 * 2 * 2 * 2 * 2 * 2 * 2 = 1024.

Это лишь несколько примеров корней, которые могут быть использованы в математике. Корни широко применяются в различных областях, таких как алгебра, геометрия и физика, для решения уравнений и нахождения неизвестных значений.

Как использовать корень в математических выражениях?

√n

Где n — число, из которого нужно извлечь корень. Степень корня может быть указана внизу символа корня. Например, если указано √mn, это означает, что нужно извлечь корень m-й степени из числа n.

Для использования корня в математических выражениях необходимо помнить следующие правила:

1. Если степень корня не указана, по умолчанию считается, что она равна 2. То есть запись √n эквивалентна √2n.
2. Можно использовать корень вместе с арифметическими операциями, такими как сложение, вычитание, умножение и деление. Например, выражение √a + √b значит, что нужно сложить корни из чисел a и b.
3. Корни можно комбинировать. Например, выражение √a + √b + √c означает, что нужно сложить корни из чисел a, b и c.
4. Корень можно использовать внутри другого корня. Например, выражение √d + √e + √f означает, что нужно сложить корни из чисел d, e и f.

Рассмотрим примеры использования корня в математических выражениях:

1. Выражение √9 + 5 означает, что нужно извлечь корень квадратный из числа 9 и прибавить к нему число 5. Результат будет равен 8, так как корень из 9 равен 3.

2. Выражение √16 + √25 означает, что нужно извлечь корень квадратный из числа 16, который равен 4, и прибавить к нему корень из числа 25, который равен 5. Результат будет равен 9.

3. Выражение √38 + 2 означает, что нужно извлечь корень третьей степени из числа 8 и прибавить к нему число 2. Результат будет приближенно равен 4,047.

Таким образом, корень является важным элементом математических выражений и может быть использован для решения различных задач.

Корень и его связь с квадратными уравнениями

Связь между корнями и квадратными уравнениями заключается в том, что решениями квадратного уравнения ax^2 + bx + c = 0 являются значения x, при которых уравнение обращается в ноль. То есть, при подстановке этих значений в уравнение, левая часть становится равной нулю.

Если уравнение имеет два различных решения, то эти значения x являются корнями квадратного уравнения. Квадратное уравнение может иметь два различных корня, один корень (если дискриминант равен нулю) или быть без корней (если дискриминант меньше нуля).

Знание связи между корнями и квадратными уравнениями позволяет решать квадратные уравнения, находить их корни и анализировать их свойства.

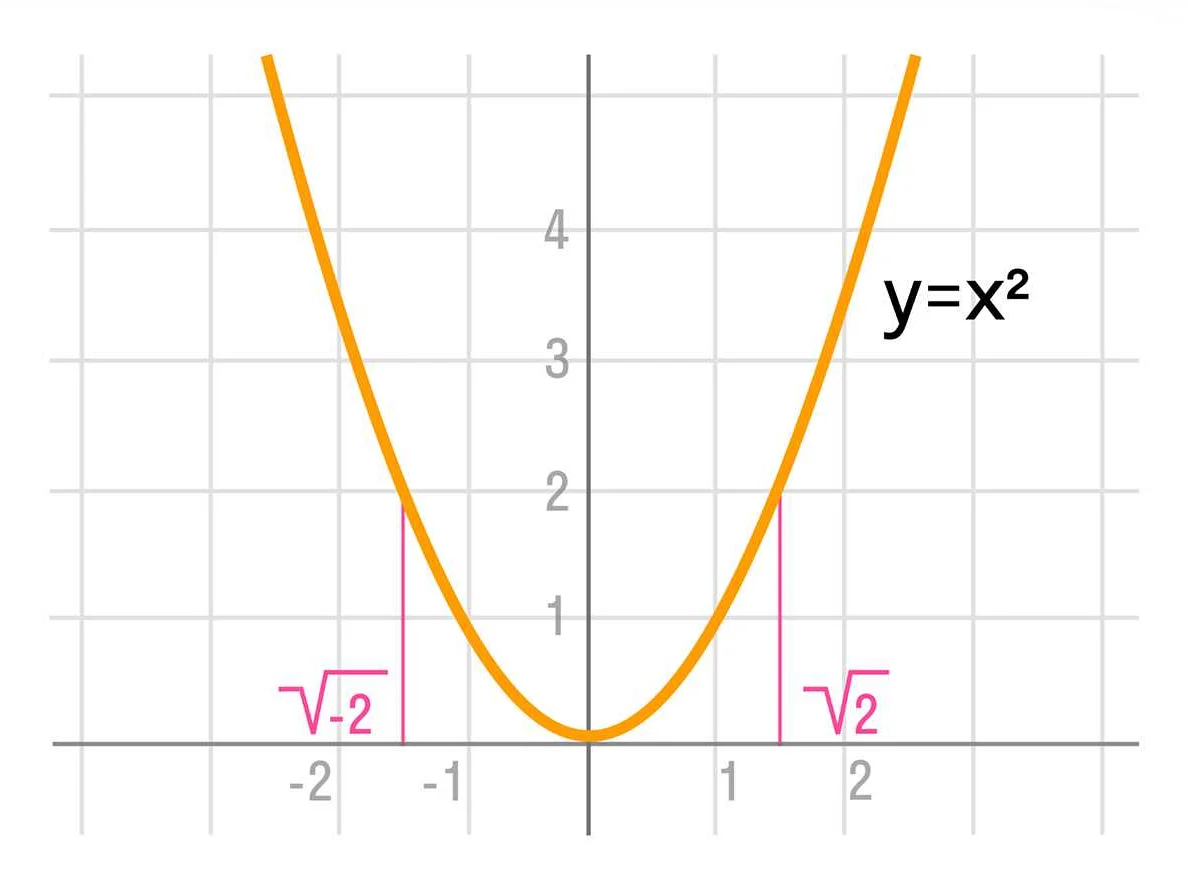
Корень и его значение в графиках функций

Корни функций имеют важное значение в анализе графиков функций. Они позволяют нам определить, где функция меняет знак и где она достигает минимума или максимума. Кроме того, корни могут помочь нам найти интервалы, на которых функция положительна или отрицательна.

Для нахождения корней функции можно использовать различные методы, включая метод подстановки, метод графических итераций, метод половинного деления и метод Ньютона-Рафсона. В зависимости от функции и условий задачи выбирается наиболее эффективный метод.

Корни функций могут иметь различные значения и влиять на форму графика функции. Они могут быть одиночными, кратными или комплексными. Одиночные корни представляют собой отдельные точки пересечения графика с осью абсцисс, кратные корни имеют касательную линию с осью абсцисс и комплексные корни являются парой точек, симметричных относительно оси абсцисс.

Изучение корней функций и их влияния на графики помогает нам лучше понимать и анализировать различные математические модели и явления в реальном мире. Корни играют важную роль в решении уравнений, определении точек пересечения графиков и нахождении экстремумов функций.

Значение корня в приложениях и реальной жизни

Корень в математике имеет широкое применение в различных областях науки и практических задачах. Вот несколько примеров, как корень используется в приложениях и реальной жизни:

1. Финансы: В финансовой сфере корень используется для расчета процентных ставок, дисконтирования денежных потоков и определения стоимости активов. Например, для оценки доходности инвестиции можно использовать формулу для расчета процентного дохода, в которой применяется корень.
2. Инженерия: В инженерии корень используется для решения различных задач, таких как настройка систем управления, расчеты электрических цепей и механических конструкций. Например, для нахождения радиуса кривизны дуги необходимо взять корень из произведения главных кривизн.
3. Физика: В физике корень используется для решения уравнений движения, нахождения значений физических величин и моделирования различных явлений. Например, для расчета скорости света можно использовать формулу, в которой присутствует корень.
4. Статистика: В статистике корень используется для нахождения среднего значения, дисперсии и других характеристик выборки. Например, для расчета стандартного отклонения необходимо взять корень из значений дисперсии.
5. Информатика: В информатике корень используется для решения задач по алгоритмам и структурам данных. Например, для определения времени выполнения алгоритма можно использовать корень для оценки сложности и эффективности алгоритма.

Таким образом, корень играет важную роль в различных областях науки и является неотъемлемой частью математического аппарата, позволяющего решать сложные задачи и моделировать различные явления в реальной жизни.