Что такое квадратный корень в математике 8 класс

Квадратный корень в математике для 8 класса — это операция обратная возведению в квадрат. Статья объясняет, как вычислять квадратный корень числа, приводит примеры задач и основные правила работы с корнями. Подробное объяснение понятия и примеры помогут учащимся 8 класса лучше понять и использовать квадратные корни в учебных задачах.

Квадратный корень – это математическая операция, обратная возведению числа в квадрат. Он позволяет найти такое число, которое при возведении в квадрат дает заданное число. Квадратный корень обозначается знаком √ перед числом, для которого он вычисляется.

В 8 классе ученики изучают основы алгебры и геометрии, и квадратный корень является одним из важных понятий в этих разделах математики. Он применяется для решения уравнений, нахождения длин сторон прямоугольных треугольников и других задач.

Например, если дано уравнение x^2 = 25, чтобы найти значение x, нужно найти квадратный корень из 25, который равен 5. Таким образом, решением уравнения будет x = 5 или x = -5.

Кроме того, квадратный корень часто используется для нахождения длин сторон прямоугольных треугольников по теореме Пифагора. Согласно этой теореме, квадрат длины гипотенузы равен сумме квадратов длин катетов. Таким образом, чтобы найти длину одного из катетов или гипотенузы, нужно извлечь квадратный корень из суммы квадратов длин известных сторон.

Квадратный корень: определение и свойства

Квадратный корень обозначается символом √. Например, √9 = 3. Если число имеет несколько квадратных корней, то обычно выбирается положительное значение.

Квадратный корень можно представить в виде десятичной дроби. Например, √2 ≈ 1,414. Но в отличие от рациональных чисел, квадратные корни могут быть иррациональными, то есть не могут быть представлены десятичной дробью или обыкновенной дробью.

Квадратный корень обладает следующими свойствами:

СвойствоФормула

Квадратный корень из произведения двух чисел равен произведению квадратных корней этих чисел	√(a * b) = √a * √b
Квадратный корень из частного двух чисел равен частному квадратных корней этих чисел	√(a / b) = √a / √b
Квадратный корень из числа, возведенного в степень, равен числу, возведенному в эту же степень	√(a^m) = a^(m/2)
Квадратный корень из квадрата числа равен самому числу	√(a^2) = a

Знание определения и свойств квадратного корня помогает в решении различных задач и упрощении выражений в алгебре. Квадратный корень широко применяется в физике, геометрии и других науках.

Как найти квадратный корень?

Для того чтобы найти квадратный корень числа, необходимо выполнить следующие шаги:

1. Выберите число, из которого нужно извлечь квадратный корень.
2. Определите, является ли число положительным или отрицательным. Квадратный корень из отрицательного числа является комплексным числом и в данном случае мы рассматриваем только случай положительных чисел.
3. Примените формулу для нахождения квадратного корня: корень из числа a, обозначается как √a.
4. Упростите выражение и найдите ответ.

Например, чтобы найти квадратный корень из числа 9, мы применяем формулу √9 = 3, так как 3 × 3 = 9.

Таким образом, чтобы найти квадратный корень, следует применить формулу и упростить выражение до получения ответа.

Корень квадратный или возведение в степень: какая разница?

Корень квадратный обозначается символом √ и используется для определения числа, которое нужно возвести в квадрат, чтобы получить данное число. Например, корень квадратный из числа 25 равен 5, так как 5 возводим в квадрат даёт 25. Корень квадратный также может быть выражен в форме десятичной дроби или бесконечной десятичной дроби.

Возведение в степень — это операция, которая позволяет умножить число само на себя заданное количество раз. Число, которое нужно возвести в степень, называется основанием, а число, на которое нужно возвести основание, называется показателем степени. Например, 2 возвести в степень 3 равно 2 * 2 * 2 = 8.

Основное отличие между корнем квадратным и возведением в степень заключается в том, что корень квадратный используется для нахождения числа, которое нужно возвести в квадрат для получения данного числа, в то время как возведение в степень используется для получения результата умножения числа само на себя заданное количество раз.

Однако, в некоторых случаях корень квадратный и возведение в степень могут быть взаимозаменяемыми. Например, корень квадратный из числа, возведённого в квадрат, будет равен исходному числу. Также, возведение числа в степень 0 даст результат 1, что эквивалентно извлечению квадратного корня из числа 1.

В итоге, хорошее понимание корня квадратного и возведения в степень позволит более глубоко изучить их свойства и применение в различных математических задачах.

Квадратный корень из отрицательного числа: мнимые числа

Мнимые числа обозначаются буквой i и имеют следующую форму: i = √(-1). Мнимая единица i является основной единицей комплексных чисел.

Комплексные числа представляют собой комбинацию мнимой и действительной частей. Они записываются в виде a + bi, где a — действительная часть, а bi — мнимая часть.

Например, √(-9) = 3i, так как 3i^2 = 3 * (-1) = -3, что эквивалентно -9.

Мнимые числа широко используются в различных областях науки и инженерии, в том числе в электротехнике, физике и компьютерной графике. Они позволяют работать с комплексными величинами и решать сложные задачи, которые не могут быть решены с использованием только действительных чисел.

Примеры вычисления квадратного корня

Квадратный корень из числа можно найти с помощью вычислительных методов, таких как метод приближений или с использованием калькулятора.

Например, чтобы найти квадратный корень из числа 9, можно возвести число в степень 0.5, так как квадратный корень — это число, возведенное в квадрат 0.5.

Таким образом, квадратный корень из 9 равен 3, так как 3 * 3 = 9.

Другой пример — квадратный корень из числа 16. В этом случае, также можно возвести число в степень 0.5:

Квадратный корень из 16 равен 4, так как 4 * 4 = 16.

Иногда может быть необходимо найти квадратный корень из числа, которое не является полным квадратом, то есть когда нет такого числа, которое возводя в квадрат, даст данное число.

Например, квадратный корень из числа 2 не является рациональным числом и его нельзя точно выразить в виде обыкновенной десятичной дроби. Однако, его можно приближенно вычислить с помощью калькулятора. Приближенное значение квадратного корня из 2 равно примерно 1.41421.

Квадратный корень в графике функции

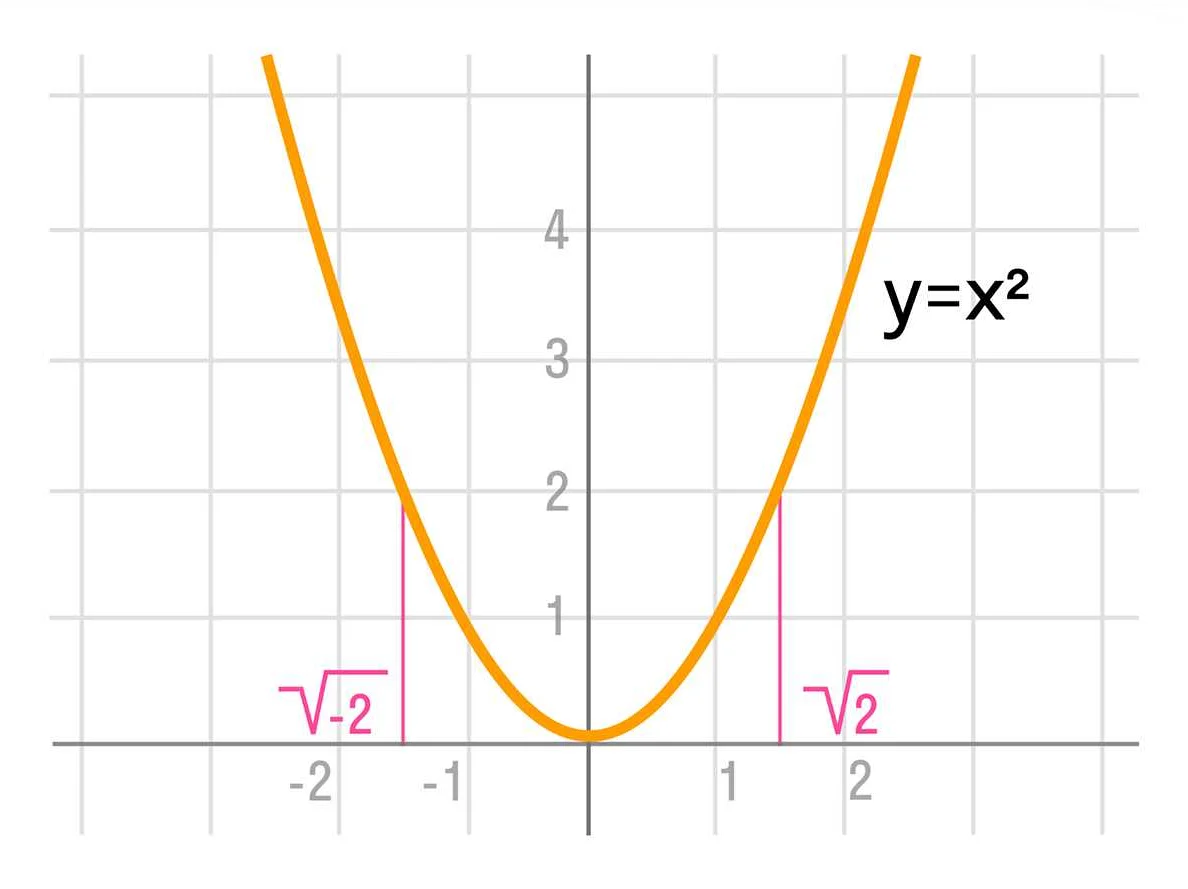
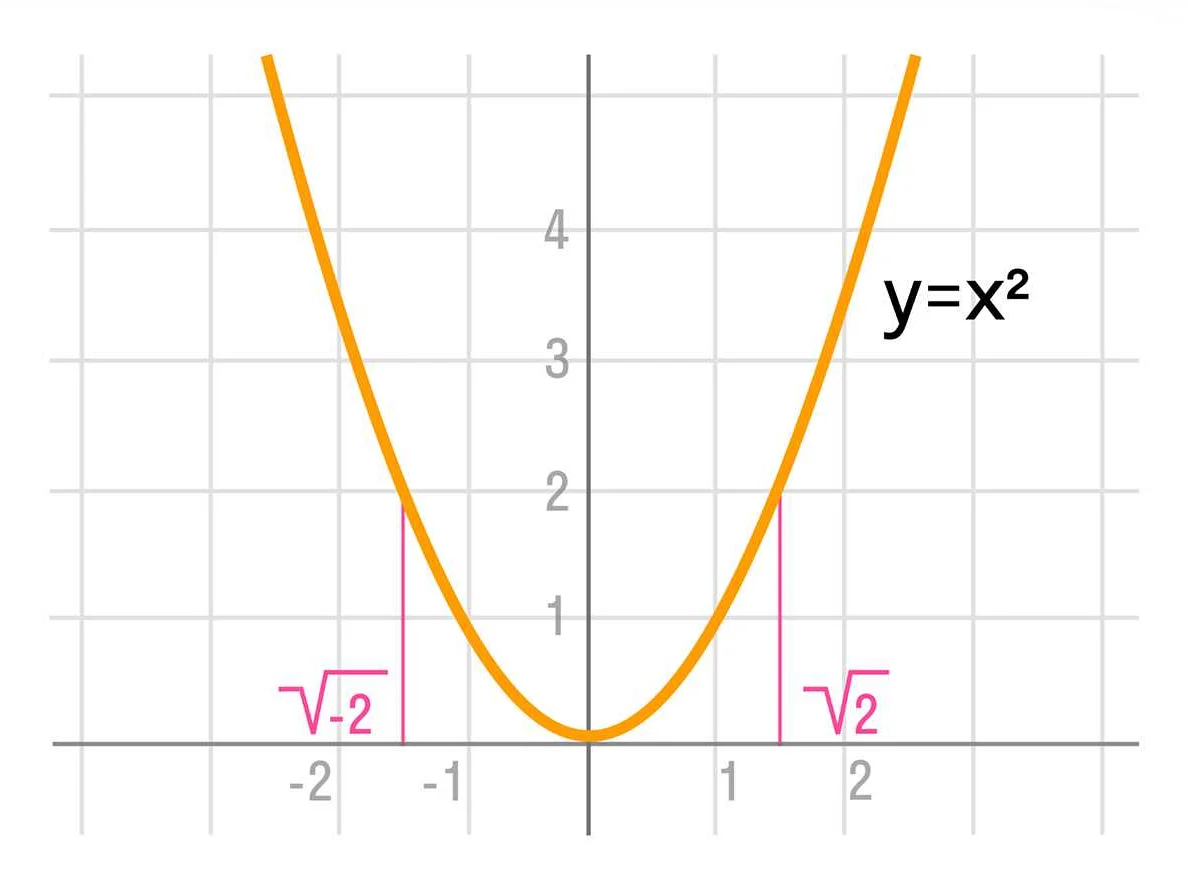
Когда мы строим график функции, координаты точек на графике соответствуют значениям функции при определенных значениях аргумента. Когда мы используем квадратный корень в функции, мы ищем значения функции, которые при подстановке в функцию и извлечении корня дадут положительный результат.

Например, рассмотрим функцию f(x) = √x, где x — аргумент функции. При построении графика этой функции мы будем искать значения функции, которые при извлечении квадратного корня дают положительный результат. Так, для значения x=4, функция f(x) = √4 = 2. Точка с координатами (4, 2) будет находиться на графике функции f(x) = √x.

Значения функции, которые при извлечении квадратного корня дают отрицательный результат, не будут учитываться при построении графика. Например, при значении x=-4, значение функции f(x) = √(-4) не существует, так как квадратный корень из отрицательного числа является комплексным числом.

xf(x)

0	0
1	1
4	2
9	3

Таблица выше показывает значения функции f(x) = √x при различных значениях аргумента x. Значения функции, которые при извлечении квадратного корня дают положительный результат, отображаются в таблице. Эти значения могут быть использованы для построения графика функции f(x) = √x.

Вопрос-ответ:

Как определить квадратный корень из числа?

Квадратный корень из числа можно определить с помощью операции извлечения корня. Квадратный корень из числа a обозначается как √a. Чтобы найти квадратный корень из числа, нужно найти такое число b, что b^2 = a. То есть, квадратный корень из числа a — это число, возведение которого в квадрат даёт a.

Как вычислить квадратный корень вручную?

Чтобы вычислить квадратный корень вручную, можно использовать метод приближений. Сначала выбирается начальное приближение, затем находятся последовательные приближения, уточняющие значение квадратного корня. Один из популярных методов — метод Ньютона. Он основан на итерационном процессе и позволяет приближенно находить квадратный корень из числа.

Какие свойства имеет квадратный корень?

Квадратный корень обладает несколькими свойствами. Например, квадратный корень из произведения двух чисел равен произведению квадратных корней этих чисел. Также квадратный корень из суммы двух чисел не всегда равен сумме квадратных корней этих чисел.

В каких случаях квадратный корень не считается?

Квадратный корень из отрицательного числа не считается вещественным числом. Вместо этого, он выражается как мнимое число, обозначаемое буквой i. Например, квадратный корень из -9 равен 3i, где i — мнимая единица.

Какие примеры можно привести для понимания квадратного корня?

Примеры использования квадратного корня можно привести в различных ситуациях. Например, при решении геометрических задач, когда нужно найти длину стороны квадрата или прямоугольника. Также квадратный корень может использоваться при решении физических задач, например, для определения скорости падения тела или вычисления длины гипотенузы прямоугольного треугольника.

Зачем нужен квадратный корень в математике?

Квадратный корень в математике используется для извлечения квадратного корня из числа. Это позволяет найти число, которое при возведении в квадрат дает заданное число. Квадратный корень может быть положительным или отрицательным, в зависимости от заданного числа.

Как найти квадратный корень из числа?

Чтобы найти квадратный корень из числа, нужно найти число, которое при возведении в квадрат дает заданное число. Для этого используются различные методы, включая методы приближенного вычисления и методы аналитической геометрии. Например, для нахождения квадратного корня из 16 можно использовать метод деления отрезка пополам, который позволяет приближенно определить значение корня.

Квадратный корень в уравнениях и неравенствах

Квадратный корень может быть использован в уравнениях и неравенствах для нахождения значений переменных, при которых эти уравнения или неравенства выполняются.

Рассмотрим первый пример. Пусть у нас есть уравнение:

x2 = 25

Для решения этого уравнения необходимо найти такое значение переменной x, при котором квадрат этого значения равен 25. То есть, нужно найти значение x, для которого выполняется условие x = √25. Решением этого уравнения будут два значения: x = 5 и x = -5.

Теперь рассмотрим пример неравенства:

x2 < 16

Чтобы найти значения переменной x, при которых это неравенство выполняется, нужно найти такие значения x, для которых квадрат этих значений будет меньше 16. То есть, нужно найти значения x, для которых выполняется условие x < √16. Решением этого неравенства будут все значения x, для которых выполняется неравенство x < 4.

Таким образом, квадратный корень позволяет находить значения переменных, при которых уравнения и неравенства выполняются.

Видео по теме: