Что такое ln в математике

Функция ln в математике является обратной к экспоненциальной функции. Она позволяет находить натуральный логарифм числа, то есть степень, в которую нужно возвести основание e, чтобы получить данное число. Узнайте, как работает функция ln и как ее использовать в различных математических задачах.

Логарифм натуральный (ln) — это одна из основных математических функций, которая широко применяется в различных областях науки и техники. Она является обратной функцией к экспоненциальной функции и позволяет решать широкий спектр задач, связанных с экспоненциальным ростом и убыванием.

Определение ln можно сформулировать следующим образом: для положительного числа x, значение ln(x) равно степени, в которую нужно возвести число e (основание натурального логарифма), чтобы получить x. Иными словами, ln(x) является показателем степени, которую нужно применить к числу e, чтобы получить x.

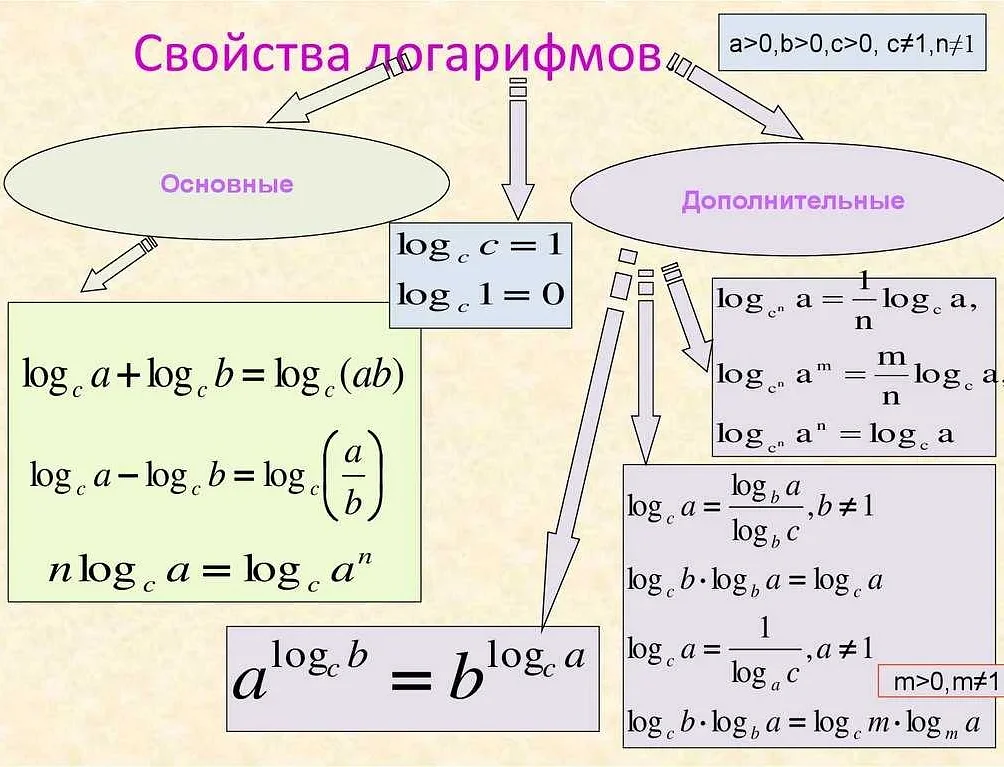
Основные свойства ln включают:

1. ln(1) = 0: натуральный логарифм от единицы равен нулю. Это свойство является следствием того, что e в степени нуля равно единице.

2. ln(e) = 1: натуральный логарифм от числа e равен единице. Также, это свойство является результатом определения ln как обратной функции к экспоненциальной функции.

3. ln(x*y) = ln(x) + ln(y): натуральный логарифм произведения двух чисел равен сумме натуральных логарифмов этих чисел. Это свойство позволяет упростить процесс вычисления логарифмов сложных выражений.

4. ln(x/y) = ln(x) — ln(y): натуральный логарифм частного двух чисел равен разности натуральных логарифмов этих чисел. Это свойство также используется для упрощения вычислений.

Логарифм натуральный является важным инструментом в математике и науке, и его свойства играют важную роль в решении различных задач и уравнений.

Понятие логарифма в математике

Логарифмы широко применяются в различных областях, таких как физика, химия, экономика, компьютерная наука и другие. Они позволяют решать различные задачи, связанные с процентными изменениями, ростом и убыванием, временем десятичного умножения и деления, а также с масштабированием и измерениями.

В математике существует несколько видов логарифмов, но одним из наиболее распространенных является натуральный логарифм, обозначаемый как ln. Натуральный логарифм использует основание e, математическую константу, примерное значение которой равно 2,71828.

Натуральный логарифм широко используется в математическом анализе, теории вероятностей, статистике и других областях. Он имеет свои особенности и свойства, которые позволяют решать различные задачи и упрощать вычисления.

Логарифмы являются важным инструментом для решения различных задач и исследования математических зависимостей. Они позволяют сжимать большие числа и упрощать сложные выражения, делая математические расчеты более удобными и понятными.

Происхождение и история ln

Исторически, натуральный логарифм был введен швейцарским математиком Леонардом Эйлером в 18 веке. Эйлер был одним из величайших математиков своего времени и внес значительный вклад в различные области математики, включая теорию чисел и математический анализ.

Эйлер установил связь между натуральным логарифмом и экспоненциальной функцией с основанием e. Он показал, что производная натурального логарифма равна обратной величине аргумента функции, то есть производная ln(x) равна 1/x. Эта связь между натуральным логарифмом и его производной играет важную роль в различных областях математики и естественных наук, таких как физика и экономика.

С течением времени натуральный логарифм стал неотъемлемой частью математических вычислений и приобрел широкое применение в различных областях. Сегодня он используется в финансовых расчетах, статистике, экономике, физике, инженерии и многих других областях, где требуется анализ экспоненциальных процессов.

Определение натурального логарифма

Натуральный логарифм определяется как обратная функция к экспоненте. Другими словами, если y = ln(x), то эквивалентное уравнение будет x = e^y, где e — основание натурального логарифма, приближенное значение которого равно примерно 2.71828.

Натуральный логарифм используется для решения разнообразных задач, таких как вычисление процентного прироста, нахождение времени удвоения, моделирование экспоненциального роста и децимации, а также в других областях математики и естественных наук.

Свойства натурального логарифма

Вот некоторые из свойств натурального логарифма:

1. Логарифм суммы равен сумме логарифмов: ln(a + b) = ln(a) + ln(b).
2. Логарифм произведения равен сумме логарифмов: ln(a * b) = ln(a) + ln(b).
3. Логарифм отношения равен разности логарифмов: ln(a / b) = ln(a) — ln(b).
4. Логарифм степени равен произведению степени и логарифма: ln(a^b) = b * ln(a).
5. Логарифм от числа 1 равен 0: ln(1) = 0.
6. Логарифм от числа e равен 1: ln(e) = 1, где e — основание натурального логарифма.

Эти свойства позволяют использовать натуральный логарифм для упрощения вычислений и решения математических задач. Он также широко применяется в областях, таких как статистика, физика, экономика и другие.

Примеры использования ln

Примеры использования ln включают:

ПримерОписание

1. ln(e)	Логарифм числа e равен 1. Это свойство логарифма, которое следует из определения экспоненциальной функции.
2. ln(1)	Логарифм числа 1 равен 0. Это также свойство логарифма, которое следует из определения экспоненциальной функции.
3. ln(x * y) = ln(x) + ln(y)	Логарифм произведения двух чисел равен сумме логарифмов этих чисел. Это свойство логарифма называется «свойство логарифма произведения».
4. ln(x / y) = ln(x) — ln(y)	Логарифм частного двух чисел равен разности логарифмов этих чисел. Это свойство логарифма называется «свойство логарифма частного».
5. ln(x^n) = n * ln(x)	Логарифм числа, возведенного в степень n, равен произведению степени n и логарифма числа x. Это свойство логарифма называется «свойство логарифма степени».

Это лишь некоторые примеры использования ln в математике. Функция ln широко применяется в физике, экономике, статистике и других науках для решения различных задач, связанных с логарифмическими функциями и экспоненциальными процессами.

Видео по теме:

Вопрос-ответ:

Что такое ln в математике?

В математике ln (натуральный логарифм) — это логарифм по основанию e (2.71828…). Он является обратной функцией экспоненциальной функции, то есть ln(e^x) = x.

Как использовать ln в математике?

Ln в математике используется для решения уравнений, вычисления производных и интегралов, а также для моделирования процессов с экспоненциальным ростом или убыванием.

Какие свойства имеет ln в математике?

Некоторые из основных свойств ln: ln(ab) = ln(a) + ln(b), ln(a/b) = ln(a) — ln(b), ln(a^b) = b * ln(a). Также ln(a) = ln(b) означает, что a = b.

Какие значения может принимать ln?

Функция ln принимает положительные значения для положительных аргументов и отрицательные значения для аргументов меньше 1. При аргументе равном 1 значение ln равно 0.

Вычисление натурального логарифма

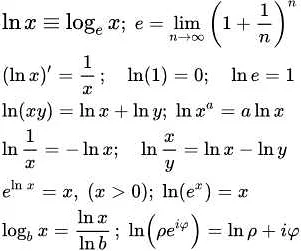
Вычисление натурального логарифма может быть выполнено с использованием различных методов, включая ряды, интегралы или приближенные алгоритмы.

Один из наиболее распространенных методов вычисления натурального логарифма основан на ряде Тейлора. Ряд Тейлора позволяет аппроксимировать функцию логарифма с заданной точностью:

ln(x) = (x — 1) — (1/2)(x — 1)^2 + (1/3)(x — 1)^3 — (1/4)(x — 1)^4 + …

Если значение аргумента x близко к 1, то ряд Тейлора может быть использован для вычисления логарифма с высокой точностью.

Однако, для значений аргумента, отличных от 1, ряд Тейлора может потребовать большое количество итераций, что затрудняет вычисление натурального логарифма. В таких случаях, можно использовать другие методы, такие как интегрирование или приближенные алгоритмы, которые основаны на различных математических свойствах функции логарифма.

Вычисление натурального логарифма является важной задачей в математике и находит широкое применение в различных областях, таких как физика, экономика, статистика и многое другое.

Применение ln в различных областях

1. Математика: В математике логарифмы широко используются для решения уравнений и вычисления сложных математических функций. Функция ln является обратной к экспоненциальной функции, что делает ее неотъемлемой частью вычислений в алгебре, анализе и дифференциальном исчислении.

2. Физика: В физике натуральный логарифм используется для описания многих естественных процессов. Он широко применяется при моделировании и анализе изменений времени, популяции, радиоактивного распада и многих других физических явлений.

3. Экономика: В экономических расчетах ln используется для измерения процентного изменения. Он может быть использован для анализа роста популяции, инфляции, экономического роста и других важных показателей.

4. Статистика: В статистике ln применяется для преобразования данных с целью получения более нормального распределения. Это позволяет проводить статистические тесты, такие как t-тест и анализ дисперсии.

5. Инженерия: В инженерных расчетах ln используется для моделирования и анализа различных процессов, таких как тепловое расширение материалов, электрические цепи и сигналы.

6. Криптография: В криптографии ln используется в различных алгоритмах шифрования и дешифрования для обеспечения безопасности данных и коммуникаций.

Таким образом, ln имеет широкий спектр применения в различных областях, что делает его одной из наиболее полезных и важных математических функций.