Основание в математике: определение и примеры

Основание в математике — это понятие, которое описывает базу или фундамент, на котором строится определенная математическая конструкция. Узнайте, что такое основание и как оно используется в различных областях математики.

Основанием в математике называют любой элемент множества, который является основой для его построения. Оно может быть как числом, так и символом, предметом, идеей или любым другим абстрактным объектом.

Основание в математических вычислениях имеет большое значение и используется в широком спектре математических дисциплин, таких как алгебра, теория чисел и геометрия. Оно играет важную роль в процессе вывода логических утверждений, формулирования гипотез и доказательств теорем.

Приведем несколько примеров использования основания в математике. В алгебре, основание является числом, которое используется для построения системы численных значений. Оно может быть любым: целым, дробным, иррациональным и т.д.

В геометрии, основание — это сторона треугольника или параллелограмма, на которую опирается фигура. Оно используется для вычисления площади и объема различных геометрических фигур.

В заключение, понимание основания в математике является важной составляющей успеха в этой дисциплине. Знание принципов создания основания иходит от логических рассуждений, что позволяет математикам строить новые теории и гипотезы, а также подтверждать имеющиеся.

Что такое основание в математике?

Основание в математике является одним из важнейших понятий. Оно используется для обозначения базиса, на котором строится какой-либо математический объект. Основание может быть определено как та часть объекта, которая играет ключевую роль в его построении и существовании.

В различных математических областях основание может варьироваться. Например, в геометрии основанием может быть сторона треугольника или параллелограмма, на которую опирается фигура. В алгебре основание может означать начальный набор аксиом, определяющий определенную теорию. В логике основание может определяться как набор правил вывода или аксиоматический набор формул.

Принцип использования основания заключается в том, что для построения и понимания какого-либо математического объекта необходимо иметь ясное представление о его основании и тех принципах, которые лежат в его основе. Например, для понимания теории множеств в математике необходимо иметь определение основных алгебраических операций над множествами, таких как пересечение и объединение, а также понимание основных аксиом и правил вывода.

В заключение, следует отметить, что понимание основания является критически важным для построения и развития математической теории. Тщательное изучение оснований позволяет увидеть связи между различными областями математики и развивать новые теории на основе уже существующих математических объектов.

Примеры использования основания в математике

1. Основание логарифма

Основание логарифма — это базис, по которому происходит расчет логарифма. Например, если основание логарифма = 2, а значение = 8, то логарифм этого числа равен 3.

2. Основание систем счисления

В системах счисления основание – это количество уникальных значений, которые может содержать конкретная цифра в заданной позиции. Например, в двоичной системе счисления основание равно 2, так как каждое место в числе может быть заполнено только двумя уникальными знаками 0 и 1. В десятичной системе счисления основание равно 10, так как десять уникальных цифр — 0, 1, 2, 3, 4, 5, 6, 7, 8 и 9 — могут занимать каждую позицию в числе.

3. Основание экспоненциальной функции

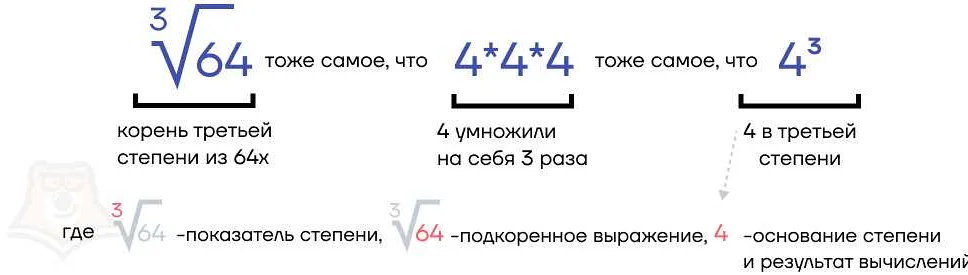
В экспоненциальной функции основание — это базис, возводящийся в степень. Экспонента является произведением основания, возводящегося в степень х. Например, если основание = 2, а х = 3, то экспонента будет равна 2^3 = 8.

4. Основание произведения корней

Основание произведения корней — это число, из которого были извлечены корни. Если два корня были извлечены из одного числа, то произведение корней будет равно данному числу, и основание будет равно этому числу. Например, корни 2 и 2/3 можно записать как √2 * √(2/3), где основание = 2/3 * 2 = 4/3.

Как выбрать правильное основание в математике?

Основание в математике — это то, на чем строится вся дальнейшая вычислительная работа. Чтобы выбрать правильное основание, нужно понимать, как именно будут использоваться числа в дальнейшем.

Первым шагом в выборе правильного основания является задание цели вычисления. Например, если нужно работать с деньгами, то правильным выбором будет десятичная система с основанием 10. Если же нужно работать с цветами, то система с основанием 16 будет более подходящей.

Важно также учитывать размерность чисел и точность вычислений. Например, если нужно работать с очень большими или очень маленькими числами, то можно использовать системы с основанием 2, 8 или 16, которые позволяют удобно работать с двоичной записью чисел.

Также стоит учитывать, какие операции будут производиться с числами в дальнейшем. Например, если нужно часто производить деление на 3, то может быть удобнее выбрать систему с основанием, кратным 3.

В итоге, выбор правильного основания в математике зависит от цели вычислений, размерности чисел, точности вычислений и операций, которые будут производиться с числами. Правильный выбор основания поможет значительно упростить дальнейшую работу с числами и сократить количество ошибок в вычислениях.

Принципы использования основания в математике

1. Основание должно быть верным

Основание в математике должно быть истинным и доказуемым фактом. Использование неверных или не доказанных оснований в математике может привести к неверным выводам и ошибочным решениям.

2. Основание должно быть однозначным и понятным

Основание должно быть ясным и понятным для читателя. Использование длинных и сложных формулировок может сбить с толку и запутать читателя, что приведет к неправильному решению задачи или выводу.

3. Основание должно быть универсальным

Основание должно быть применимо не только к конкретной задаче, но и к широкому диапазону задач в математике. Использование узко специализированных оснований может ограничить использование решения задачи в других областях математики.

4. Основание должно быть логически связанным с задачей

Основание должно быть логически связанным с задачей и последующим решением. Использование нерелевантных оснований может привести к неправильным выводам и ошибочным решениям.

5. Основание должно быть проверяемым

Основание должно быть проверяемым и доказуемым. Использование не доказуемых оснований может привести к неправильным выводам и ошибочным решениям.

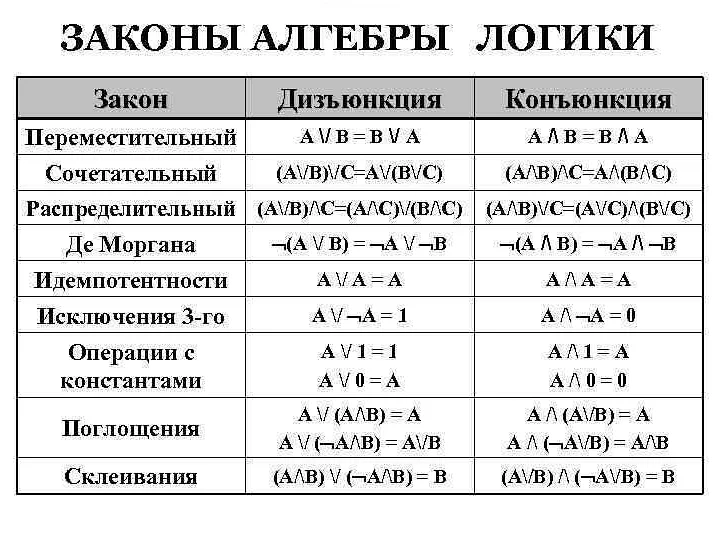
Основание в математической логике

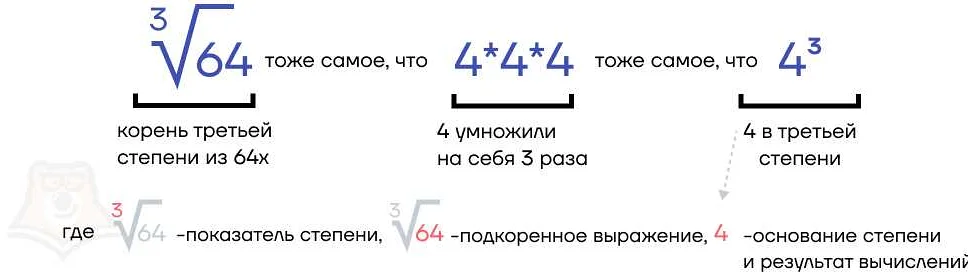
В математической логике основание — это формальная система, которая определяет правила вывода и ограничения на используемые символы и выражения. Она является основой для построения формальных доказательств и рассуждений в математике, позволяя получать новые истины на основе уже известных.

Основание обычно состоит из трех компонентов:

• Алфавит — конечный набор символов, которые могут быть использованы в выражениях. Часто это буквы, цифры и знаки операций;
• Синтаксис — набор правил, определяющих, как комбинировать эти символы, чтобы получить корректные выражения. Например, для использования знака «+» необходимо иметь два операнда слева и справа от него;
• Семантика — правила трактовки этих выражений в терминах истинности. Например, выражение «1+1=2» истинно в обычной арифметике, но ложно в модулярной арифметике по модулю 2.

Примерами формальных систем являются классическая логика высказываний, логика первого порядка, теория множеств и т. д. В каждой из этих систем определены различные правила вывода и ограничения, которые позволяют получать новые истины на основе аксиом и уже полученных результатов.

Важно понимать, что формальные системы являются лишь моделями, которые упрощают нашу работу с математическими концепциями. Они не в полной мере передают сложность и противоречивость реального мира, поэтому не следует абсолютизировать результаты, полученные в рамках какой-либо формальной системы.

Как правильно использовать основание в геометрии?

Основание в геометрии – это один из самых важных элементов, который позволяет рассчитывать различные параметры геометрических фигур. Существуют различные принципы использования основания в геометрии, о которых нужно знать каждому учащемуся математики.

1. Основание при вычислении площади фигур. Для вычисления площади треугольника, прямоугольника, трапеции и других фигур, необходимо знать длину их основания. Основание – это сторона фигуры, на которую опирается фигура и которая определяет ее форму.
2. Основание при решении задач на нахождение высоты. Высота треугольника – это линия, которая проведена из вершины треугольника к противоположной стороне и перпендикулярна ей. Для вычисления высоты треугольника необходимо знать его основание и площадь.
3. Основание при решении задач на нахождение площади боковой поверхности. Для вычисления площади боковой поверхности пирамиды или конуса необходимо знать длину их основания и высоты.

Важно понимать, что правильное использование основания в геометрии является ключом к правильному решению математических задач. При выполнении заданий необходимо уметь определять основание для каждой фигуры, а также знать, как правильно использовать его для решения задач.

Основание в тригонометрии: примеры и принципы использования

Основание в тригонометрии — это сторона прямоугольного треугольника, лежащая напротив прямого угла. Она часто обозначается буквой c.

Основание используется для вычисления других тригонометрических функций, таких как синус, косинус и тангенс.

Пример: Рассмотрим прямоугольный треугольник со сторонами a=3, b=4 и c=5. Тогда основание равно 4.

СторонаЗначение

a	3
b	4
c	5

Принцип использования:

• Основание — это сторона прямоугольного треугольника, лежащая напротив прямого угла.
• Обычно основание обозначается буквой c.
• Основание используется для вычисления других тригонометрических функций, таких как синус, косинус и тангенс.
• Для вычисления тригонометрических функций с помощью основания необходимо знать значение угла между основанием и стороной треугольника.

Использование основания является важным элементом в решении задач тригонометрии и нахождения неизвестных значений в прямоугольных треугольниках.

Как использовать основание в алгебре и анализе?

Основание в математике — это число или выражение, на которое возведено число или переменная. Оно часто используется в алгебре и анализе, чтобы более эффективно решать уравнения и преобразовывать выражения. Вот несколько способов использования основания:

• Использование основания в алгебре: Если у вас есть уравнение вида a^x = b, вы можете найти значение x, возведя обе части уравнения в основание a. Например, если a = 2 и b = 16, то 2^x = 16 => x = 4.
• Использование основания в логарифмах: Логарифм — это инструмент, используемый для обратного преобразования числа в степень. Если у вас есть выражение вида log_a b = c, то c — это логарифм числа b по основанию a. Чтобы найти b, достаточно вознести a в степень c. Например, если log_2 8 = 3, то 2^3 = 8.
• Использование основания в дробных степенях: Когда вы работаете с дробными степенями, вы можете использовать основание, чтобы приблизительно найти значения. Например, если a = 5 и b = 1/3, то вы можете приблизительно найти 5^(1/3) путем возведения 5 в ближайшую к 1/3 степень, равную 2. Можно проверить, что 5^2 = 25, а 25^(1/3) = 2.92.

Использование основания может существенно упростить ваше решение уравнений и выражений. Этот инструмент особенно полезен при работе с логарифмами, поскольку он может помочь вам перенести значения из одной формы записи в другую. Не забывайте, что основание может принимать любое значение, поэтому экспериментируйте и продолжайте обучение!

Видео по теме:

Вопрос-ответ:

Что такое основание в математике и зачем оно нужно?

Основание — это тот элемент, на котором строится математическое доказательство. Оно также может быть называно «гипотезой» или «аксиомой» и служит для того, чтобы получить новые математические выводы на основе уже известных. Основание часто используется в математических науках, включая геометрию, алгебру и теорию чисел.

Какие примеры оснований существуют в математике?

Один из наиболее известных примеров основания в математике — это аксиома параллельных линий в геометрии, которая устанавливает, что если две прямые линии пересекают третью, то углы, образованные этим пересечением, будут равны. Еще один пример основания — это аксиома выбора, которая утверждает, что при выборе элемента из набора мы всегда можем выбрать какой-то элемент. Этот принцип часто используется в анализе и теории множеств.

Можно ли проверить правильность выбранного основания?

Проверить правильность выбранного основания можно в той мере, в которой оно соответствует логической завершенности и не противоречит другим, уже установленным основаниям. В случае параллельных линий, например, если бы было найдено противоречие, то было бы необходимо пересмотреть это как основание, а в случае аксиомы выбора — проверить, что она не противоречит другим аксиомам, используемым в доказательстве.

Что делать, если не уверен/а в выборе основания при решении задачи?

Если не уверен/а в выборе основания, то нужно провести анализ доступных вариантов и оценить их логическую состоятельность и подходящесть к задаче. Если не удалось выбрать основание в рамках задачи, то, возможно, необходимо вернуться к описанию задачи и выделить более конкретные параметры, чтобы составить более точное основание.

Могут ли различные научные области использовать одинаковые основания в своих доказательствах?

Да, это возможно. Научные области могут использовать одинаковые основания в своих доказательствах, если это основание их научной теории. Математические аксиомы, например, часто используются в различных областях, таких как физика, их механика, биология и научные исследования. Использование общих оснований в различных областях может помочь в разработке связанных теорий и усилении связей между различными областями знаний.

Как основание может влиять на результат математического доказательства?

На выбор основания может влиять результат математического доказательства. Это связано с тем, что правильное выбор основания может помочь получить верный результат, в то время как неправильное основание может привести к неверному результату, противоречию или недостаточно логически обоснованному выводу. Правильное выбор основания учитывает все необходимые условия и начальные данные, а также цель доказательства.

Может ли одно и то же доказательство иметь разные основания?

Да. Одно и то же доказательство может иметь разные основания, если эти основания эквивалентны. Это значит, что они могут быть заменены друг на друга в любой части доказательства, сохраняя его логическую верность. Например, если доказательство использует аксиому двойства в алгебре, то можно использовать также и аксиому отражения, поскольку они эквивалентны друг другу.

Различные типы оснований в математике

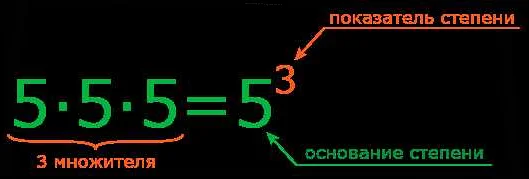
Основание в математике — это число или выражение, которое является начальным элементом в математическом доказательстве. Существуют различные типы оснований в математике, которые используются в разных областях математики, включая алгебру, геометрию и анализ.

Основания в алгебре:

• Натуральные числа.
• Целые числа.
• Рациональные числа.
• Действительные числа.
• Комплексные числа.

В алгебре основание используется для доказательства алгебраических утверждений и теорем. Например, в доказательстве теоремы о двух квадратах основанием может быть использовано целое число.

Основания в геометрии:

• Отрезки.
• Углы.
• Плоские фигуры (треугольники, прямоугольники, круги и т.д.).
• Тела (кубы, шары, цилиндры и т.д.).

В геометрии основание часто используется для доказательства геометрических утверждений и теорем. Например, для доказательства теоремы Пифагора может быть использовано основание в виде прямоугольного треугольника.

Основания в анализе:

• Определения.
• Принципы.
• Теоремы.
• Формулы.

В анализе основание широко используется для доказательства математических утверждений и теорем. Например, основание в виде определения может использоваться для доказательства теоремы о пределах функций.

Тип основанияОбласть использованияПримеры

Алгебраическое	Алгебра	Доказательство теоремы о двух квадратах основанием может быть использовано целое число.
Геометрическое	Геометрия	Для доказательства теоремы Пифагора может быть использовано основание в виде прямоугольного треугольника.
Аналитическое	Математический анализ	Основание в виде определения может использоваться для доказательства теоремы о пределах функций.

В общем, выбор правильного основания очень важен для успешного доказательства утверждений в математике.

Как избежать ошибок при использовании основания в математике?

Ошибки в использовании основания могут привести к неверным результатам и ошибочным выводам. Чтобы избежать ошибок, нужно следовать нескольким принципам:

• Проверять основание перед использованием. Убедитесь, что основание выбрано правильно, и вы знаете, что это означает.
• Никогда не менять основание без необходимой причины. Если вам нужно менять основание, убедитесь, что вы понимаете последствия этого действия и знаете, как это может повлиять на решаемую задачу.
• Не полагаться только на основание. Основание может быть полезным инструментом для работы с числами, но оно не является ключом к пониманию всех аспектов математики. Не забывайте обращаться к другим методам решения задач и альтернативным подходам.
• Обращаться к материалам для дополнительной помощи. Если у вас возникли трудности при использовании основания, обратитесь к материалам для дополнительной помощи. Курсы, учебники, онлайн-ресурсы могут предоставить полезную информацию и подробно разобрать понятия и принципы.

Следуя этим принципам, можно минимизировать риски ошибок при использовании основания и добиваться более точных и правильных результатов.