Что такое степень в математике определение
Содержимое
- 1 Что такое степень в математике определение
- 1.1 Степень в математике: основная концепция и определение
- 1.2 Как правильно читать степень и как она записывается
- 1.3 Основные свойства степеней и их применение
- 1.4 Что такое показатель и база в степени
- 1.5 Как упрощать степени и выполнять операции с ними
- 1.6 Что означает отрицательная степень и как ее вычислять
- 1.7 Степени с рациональными показателями: примеры и приложения
- 1.8 Примеры решения задач с использованием степеней
- 1.9 Видео по теме:
Степень в математике — это операция, при которой число умножается само на себя заданное количество раз. Узнайте, как определить степень числа и как использовать ее в математических вычислениях.
Степень – важное понятие в математике, которое возникает при умножении числа на себя несколько раз. Она позволяет удобно записывать и работать с очень большими и очень маленькими числами. В математике степень обозначается с помощью знака «^» и двух чисел: основания и показателя. Основание – это число, которое нужно умножить на себя несколько раз, а показатель указывает, сколько раз нужно умножить основание на само себя.
Степень может быть положительной, отрицательной и нулевой. Положительная степень означает, что число будет умножаться само на себя столько раз, сколько указано в показателе. Например, 2 в степени 3 равно 2 * 2 * 2 = 8. Отрицательная степень указывает, что число будет делиться на само себя столько раз, сколько указано в показателе. Например, 2 в степени -2 равно 1 / (2 * 2) = 1 / 4 = 0,25. Нулевая степень равна 1 для любого числа, кроме нуля.
Степени обладают несколькими основными свойствами. Одно из них – свойство умножения степени с одним и тем же основанием. Если у нас есть число а в степени m и его нужно умножить на число а в степени n, то это равносильно умножению основания на себя m + n раз. Например, 2 в степени 3 умножить на 2 в степени 2 равно 2 в степени (3 + 2) = 2 в степени 5.
Степень в математике: основная концепция и определение
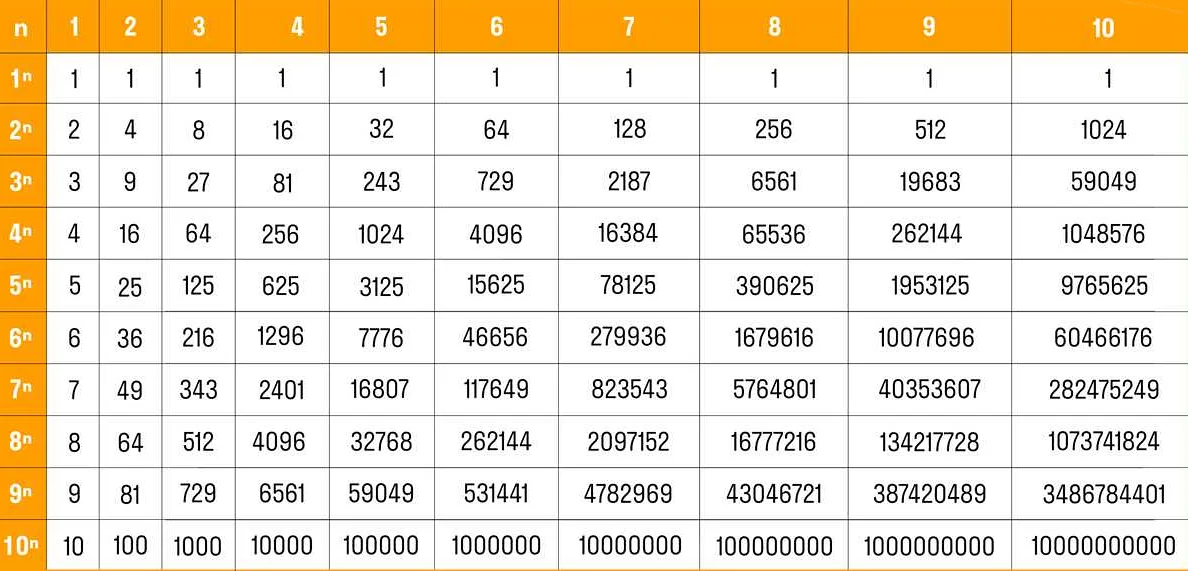
Определение степени: если a — число (основание степени) и n — натуральное число (показатель степени), то a в степени n (обозначается a^n) равно произведению n сомножителей, каждый из которых равен a.
Например, 2 в степени 3 (2^3) равно 2 * 2 * 2 = 8.
Степень имеет свои основные свойства:
| Свойство степени | Формулировка | Пример |
| Свойство умножения | a^m * a^n = a^(m + n) | 2^3 * 2^4 = 2^(3 + 4) = 2^7 |
| Свойство возведения в степень единицы | a^1 = a | 3^1 = 3 |
| Свойство возведения в нулевую степень | a^0 = 1 | 5^0 = 1 |
| Свойство возведения в отрицательную степень | a^(-n) = 1 / a^n | 2^(-3) = 1 / 2^3 = 1 / 8 |
Степень используется в различных областях математики, физики и техники для представления и работы с большими числами, а также для решения различных задач и уравнений.
Как правильно читать степень и как она записывается
Степень можно прочитать как «число в степени показатель». Например, степень 2 в третьей степени читается как «2 в кубе» или «2 в третьей».
Степень обычно записывается с использованием знака «^» между основанием и показателем. Например, степень 2 в третьей степени записывается как 2^3.
Также существует возможность записывать степень с использованием специальных символов, которые являются частью символьной нотации. Например, степень 2 в третьей степени может быть записана как 2³.
Для чтения степени в записи с использованием символьной нотации, читают основание, а затем показатель. Например, запись 2³ читается как «два в кубе» или «два в третьей степени».
Важно помнить, что степень может быть как положительной, так и отрицательной. Положительная степень показывает, сколько раз нужно умножить число на само себя, а отрицательная степень показывает, сколько раз нужно разделить число на само себя.
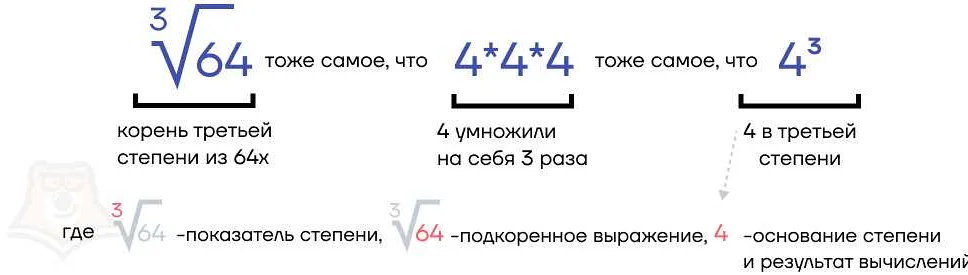
Также степень может быть дробной, что показывает, что число нужно извлечь корень соответствующей степени.
Основные свойства степеней и их применение

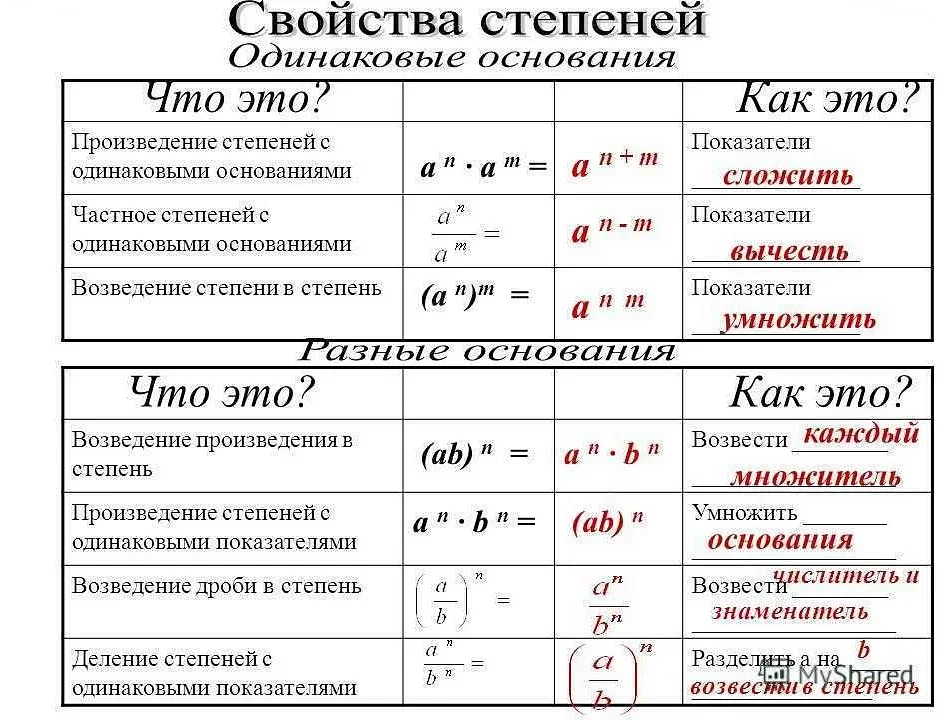
- Свойство умножения степеней с одинаковым основанием: если у нас есть две степени с одинаковым основанием, то их можно перемножить, сохраняя это же основание и складывая показатели степени. Например, am * an = am+n.
- Свойство деления степеней с одинаковым основанием: если у нас есть две степени с одинаковым основанием, то их можно разделить, сохраняя это же основание и вычитая показатели степени. Например, am / an = am-n.
- Свойство возведения степени в степень: если у нас есть степень, которую нужно возвести в другую степень, то можно перемножить показатели степени. Например, (am)n = am*n.
- Свойство отрицательной степени: если у нас есть число в отрицательной степени, то его можно записать как обратное число в положительной степени. Например, a-n = 1 / an.
- Свойство степени с показателем равным нулю: любое число, кроме нуля, возводимое в степень с показателем равным нулю, равно единице. Например, a0 = 1, при a ≠ 0.
Основные свойства степеней позволяют упрощать математические выражения, решать уравнения, проводить доказательства и проводить различные операции с числами и переменными. Знание этих свойств является основой для изучения более сложных математических концепций и их применения в реальных задачах.
Что такое показатель и база в степени
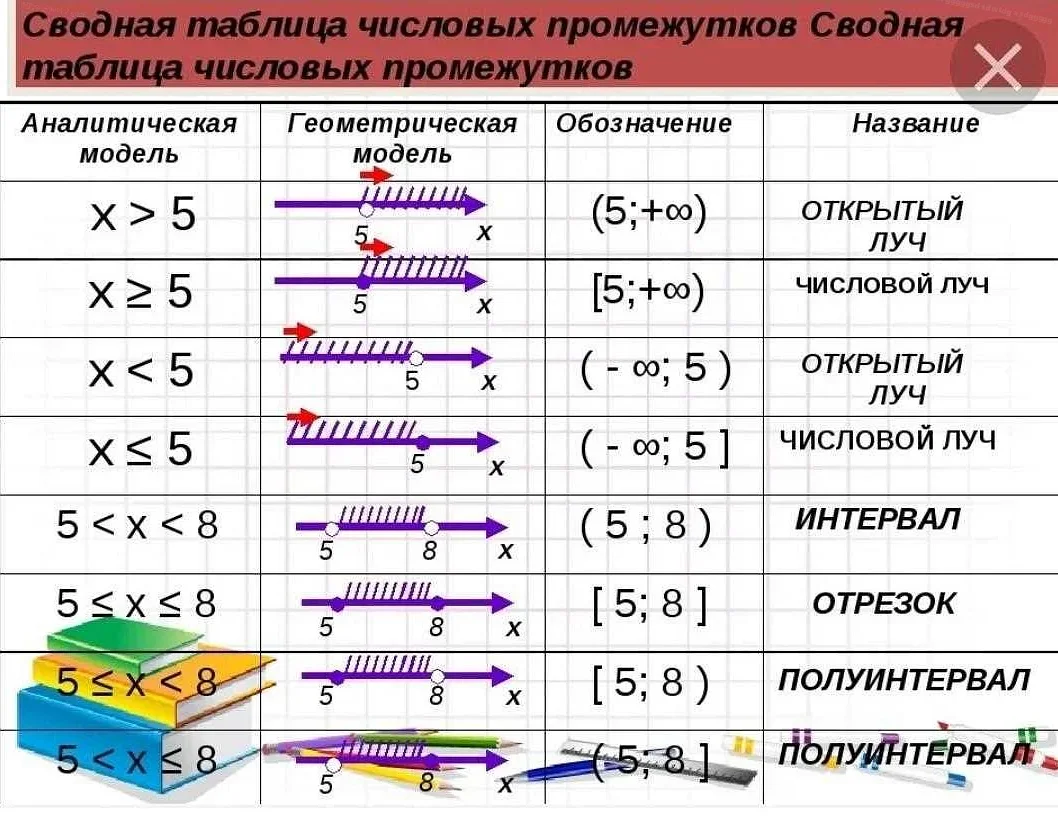
База — это число, которое нужно возвести в степень. Оно может быть любым действительным числом, положительным или отрицательным.
Показатель — это число, которое указывает, сколько раз нужно умножить базу на себя. Он должен быть натуральным числом, то есть положительным и целым. Показатель может быть также равен нулю или отрицательному числу.
Если показатель равен нулю, то результат степени всегда равен 1, независимо от значения базы. Если показатель равен отрицательному числу, то результат степени можно получить, взяв обратное значение от результата степени с положительным показателем. Например, 3^-2 равно 1/3^2 = 1/9.
Понимание базы и показателя в степени важно для понимания и работы с другими операциями, связанными со степенями, такими как умножение степеней с одинаковой базой и сложение степеней с одинаковым показателем.
Как упрощать степени и выполнять операции с ними
Упрощение степеней позволяет сократить сложные выражения и упростить их до более простых форм. Операции с степенями включают в себя умножение, деление, возведение в степень и извлечение корня.
Для упрощения степеней можно использовать следующие основные свойства:
СвойствоПримерОбъяснение
| Свойство умножения степеней с одинаковыми основаниями | am * an = am+n | При умножении степеней с одинаковыми основаниями их показатели суммируются |
| Свойство деления степеней с одинаковыми основаниями | am / an = am-n | При делении степеней с одинаковыми основаниями их показатели вычитаются |
| Свойство возведения степени в степень | (am)n = am*n | При возведении степени в степень показатели умножаются |
| Свойство извлечения корня из степени | (√am)n = am/n | При извлечении корня из степени показатель делится на корень |
При выполнении операций с степенями необходимо учитывать приоритетность операций и правила знаков. Также можно использовать скобки, чтобы группировать части выражений и упрощать их.
Что означает отрицательная степень и как ее вычислять

Отрицательная степень в математике означает, что число возводится в обратную степень и затем инвертируется. Например, если у нас есть число a и отрицательная степень n, то a в степени -n равно 1, деленное на a в степени n.
Чтобы вычислить отрицательную степень, нужно сначала найти число в обратной степени. Для этого возводим число в положительную степень, а затем берем обратное значение. Например, чтобы вычислить 2 в степени -3, мы сначала возводим 2 в степень 3, что равно 8, а затем берем обратное значение, получая 1/8.
Если число находится в знаменателе дроби, в отрицательную степень нужно возвести как числитель, так и знаменатель. Например, чтобы вычислить 1/3 в степени -2, мы возводим 1 в степень -2, получая 1, а также возводим 3 в степень -2, получая 1/9. Затем делим числитель на знаменатель и получаем результат 9.
ПримерВычислениеРезультат
| 2-3 | 1 / 23 | 1 / 8 |
| (1/3)-2 | (12) / (32) | 9 |
Степени с рациональными показателями: примеры и приложения
Примером степени с рациональным показателем может быть следующее выражение: 2^(1/2). Здесь число 2 является основанием, а 1/2 – показателем. В данном случае степень равна квадратному корню из числа 2.
Степени с рациональными показателями имеют множество приложений в различных областях. Например, в физике они используются при решении задач, связанных с экспоненциальным ростом или затуханием. Также степени с рациональными показателями могут быть полезны при работе с пропорциями и прогрессиями.
Примеры решения задач с использованием степеней
Степени широко применяются в математике для решения различных задач. Рассмотрим несколько примеров:
Пример 1: Рассмотрим задачу о вычислении площади квадрата со стороной a. Площадь квадрата равна a во второй степени (a^2).
Пример 2: Рассмотрим задачу о вычислении объема параллелепипеда с длиной a, шириной b и высотой c. Объем параллелепипеда равен a в первой степени (a), умноженное на b в первой степени (b), умноженное на c в первой степени (c) (a * b * c).
Пример 3: Рассмотрим задачу о вычислении суммы вклада после t лет при простых процентах. Формула для вычисления суммы вклада: S = P * (1 + r)^t, где S — сумма вклада, P — начальная сумма вклада, r — годовая процентная ставка, t — количество лет. В данной формуле степень (1 + r)^t используется для учета процентов на протяжении t лет.
Пример 4: Рассмотрим задачу о вычислении скорости движения объекта. Формула для вычисления скорости: v = s / t, где v — скорость, s — пройденное расстояние, t — время. Если пройденное расстояние s выражено в метрах, а время t в секундах, то скорость v будет выражаться в метрах в секунду. В данном примере степень неявно используется, так как скорость вычисляется делением расстояния на время.
Это лишь некоторые примеры использования степеней в математике. Степени очень полезны и применяются во многих других областях, таких как физика, экономика, компьютерные науки и т. д.
Видео по теме:
Что такое степень в математике?
Степень в математике — это операция возведения числа в натуральную степень. Если число a возведено в степень n, то результатом будет произведение числа a на себя n раз.
Как записать степень в математике?
Степень в математике можно записать с помощью знака «^». Например, a^n означает, что число a возводится в степень n.
Как вычислить степень числа?
Для вычисления степени числа нужно умножить это число само на себя столько раз, сколько указано в степени. Например, чтобы вычислить 2 в степени 3, нужно умножить 2 на себя 3 раза: 2 * 2 * 2 = 8.
В каких случаях степень может быть отрицательной?
Степень может быть отрицательной, если число, возводимое в степень, является десятичной дробью или дробью. В этом случае, чтобы вычислить степень, нужно взять обратное число и возвести его в положительную степень. Например, чтобы вычислить 2 в степени -3, нужно взять обратное число 1/2 и возвести его в степень 3: (1/2)^3 = 1/(2^3) = 1/8.
Что такое степень в математике?
Степень в математике — это операция, которая позволяет возводить число в некоторую степень. Степень представляет собой произведение данного числа на себя заданное количество раз.

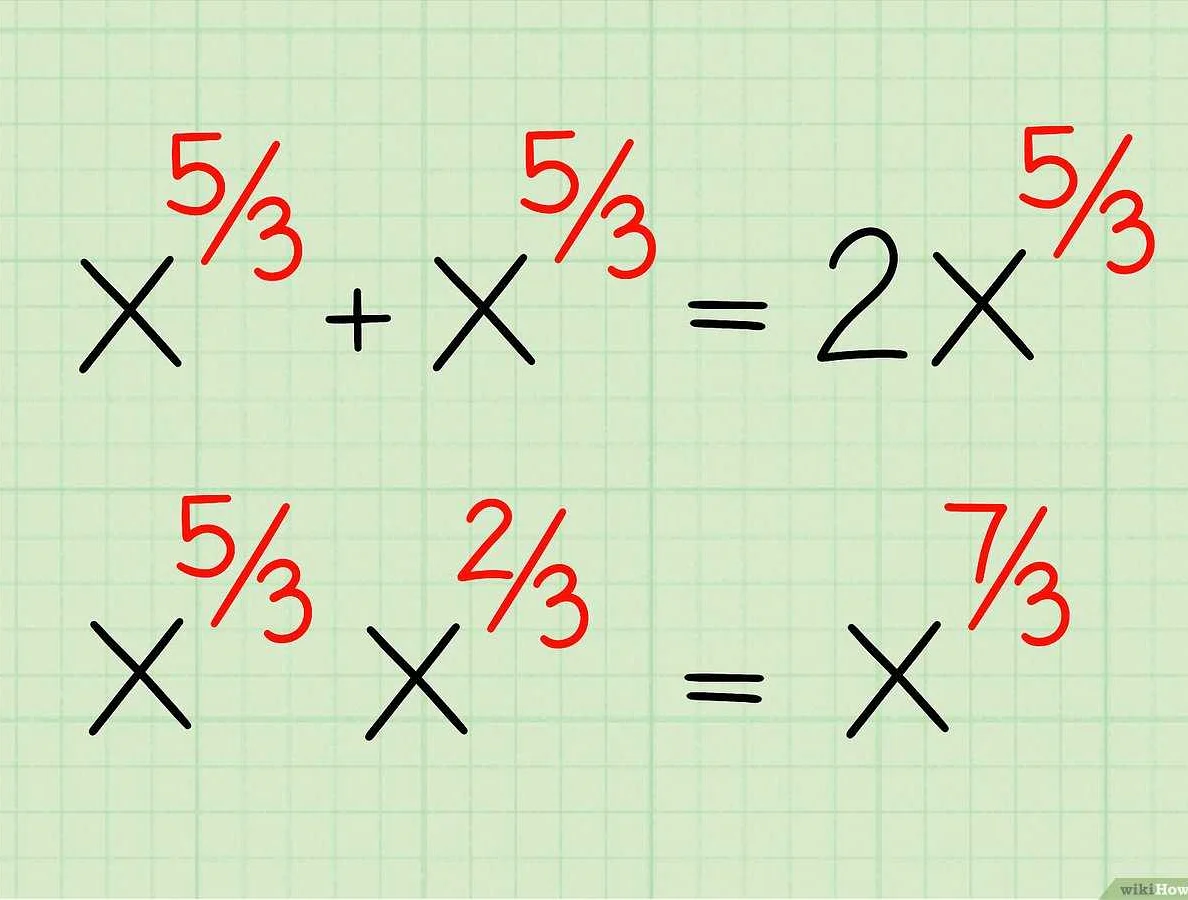

Спасибо автору статьи за понятное и подробное описание понятия степень в математике. Я давно интересуюсь этой наукой, но всегда было немного непонятно, что такое степень и как с ней работать. Особенно мне понравилось объяснение основных свойств степеней, таких как умножение и деление. Теперь я легко могу решить простые уравнения с использованием степени. Эта информация будет полезна и в повседневной жизни, например, при расчете процентов или налогов. Я очень благодарен за такую полезную статью!
Статья очень понравилась! Она очень доступно и понятно объясняет, что такое степень в математике. Математика всегда казалась для меня сложной и непонятной, но благодаря этой статье я стала лучше понимать, как работает степень и как ее применять. Особенно понравилось, что автор подробно рассказал о свойствах степени, таких как ассоциативность и коммутативность. Теперь я смогу более уверенно решать задачи и использовать степень в повседневной жизни. Спасибо за такую полезную статью! Жду еще подобных материалов.