Что такое масштаб в математике 4 класс

Масштаб в математике 4 класс – это понятие, которое помогает сравнивать размеры объектов на рисунке с их реальными размерами. В данной статье вы узнаете, как определить масштаб и как им пользоваться при решении задач.

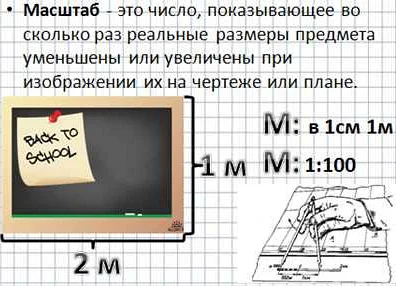
Масштаб – это понятие, которое используется в математике для измерения и сравнения объектов. В 4 классе ученики изучают масштаб как величину, позволяющую установить соотношение между длиной или размером реального предмета и его изображения на плоскости.

Масштаб может быть представлен в виде доли или отношения. Например, масштаб 1:100 означает, что каждый сантиметр на плоскости соответствует 100 сантиметрам в реальности. Если масштаб представлен в виде отношения, то он записывается как 1/100. Чем больше числитель, тем больше масштаб, и наоборот.

Пример: Пусть у нас есть рисунок домика, на котором одна клетка в сетке соответствует 1 метру в реальности. Если нам нужно узнать, сколько метров в домике, мы можем использовать масштаб. Если 1 клетка на рисунке соответствует 1 метру, то мы можем просто посчитать, сколько клеток занимает домик и умножить на 1 метр.

Изучение масштаба в математике помогает ученикам развивать навыки анализа и пространственного мышления. Этот навык также полезен в повседневной жизни, например, при оценке размеров объектов на картах или планах зданий.

Масштаб — определение и основные понятия

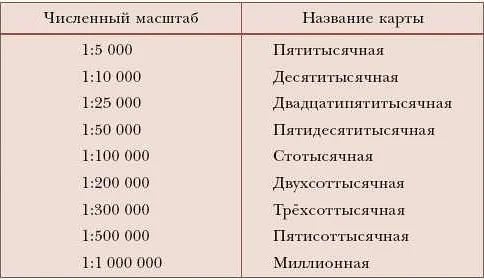
Основные понятия, связанные с масштабом:

1. Масштабная линейка: это отрезок на рисунке, который представляет определенную длину в реальном мире. Она помогает определить, какие размеры объектов на рисунке соответствуют реальным размерам.
2. Увеличение: это увеличение размеров объекта в изображении по сравнению с его реальными размерами. Увеличение обычно обозначается числом, большим 1.
3. Уменьшение: это уменьшение размеров объекта в изображении по сравнению с его реальными размерами. Уменьшение обычно обозначается числом, меньшим 1.

Например, если на рисунке масштабная линейка длиной 5 см соответствует реальной длине 1 м, то масштаб будет равен 1:20. Это означает, что каждый сантиметр на рисунке соответствует 20 сантиметрам в реальном мире.

Использование масштаба позволяет более удобно и точно работать с изображениями, делать точные измерения и анализировать объекты разного размера. Понимание основных понятий и правил масштабирования поможет в решении задач и работе с графиками и диаграммами.

Видео по теме:

Как использовать масштаб в задачах

В задачах, связанных с масштабом, часто используются масштабные модели. Например, при изучении карты города масштаб показывает, какое расстояние на карте соответствует определенному расстоянию в реальном мире. Также масштаб может использоваться при изучении процессов увеличения или уменьшения, например, при решении задач на пропорции.

Для использования масштаба в задачах, вам необходимо:

1. Определить, что именно вы хотите измерить или представить.
2. Определить масштаб, который будет наиболее удобным для работы. Например, если вы хотите измерить расстояние между двумя городами, может быть удобно выбрать масштаб, в котором один сантиметр на карте будет соответствовать 100 километрам в реальном мире.
3. Применить масштаб к объектам или явлениям, которые вы хотите измерить или представить. Например, если вы хотите представить длину автомобиля на чертеже, вы должны умножить его реальную длину на масштаб.
4. Использовать полученные результаты для решения задачи или для получения нужной информации.

Важно помнить, что масштаб может быть задан как числом, так и словесно. Например, масштаб 1:100 означает, что одна единица измерения на карте соответствует 100 единицам в реальном мире.

Использование масштаба в задачах помогает нам лучше понять и представить информацию, делает ее более наглядной и удобной для работы. Это важный навык, который помогает нам развивать математическое мышление и решать различные задачи в нашей повседневной жизни.

Масштаб в геометрии и изображениях

Масштаб в геометрии используется для измерения и построения фигур на плоскости. Например, если на чертеже дома один сантиметр соответствует одному метру в реальности, то это масштаб 1:100. Это означает, что все размеры на чертеже уменьшены в 100 раз по сравнению с реальными размерами.

Масштаб в изображениях на компьютере или фотографиях также позволяет изменять размеры объектов. Например, при уменьшении масштаба фотографии, все объекты на ней будут меньше, а при увеличении масштаба – больше. Это часто используется при обработке изображений или при просмотре фотографий на экране.

Для наглядного представления масштаба в геометрии и изображениях можно использовать таблицу. В таблице указываются размеры объектов на рисунке, их реальные размеры и соответствующий масштаб. Такая таблица помогает лучше понять, насколько объекты уменьшены или увеличены на рисунке.

ОбъектРазмер на рисункеРеальный размерМасштаб

Дом	10 см	10 м	1:100
Автомобиль	5 см	4 м	1:80
Дерево	3 см	6 м	1:200

Таким образом, масштаб в геометрии и изображениях играет важную роль, позволяя представить объекты в уменьшенном или увеличенном масштабе для удобства их изучения или визуализации.

Примеры использования масштаба в математике

Пример 1:

Представьте, что вы строите план вашей комнаты на листе бумаги. Чтобы все поместилось, вы решаете использовать масштаб 1 см – 1 метр. То есть каждый сантиметр на бумаге будет соответствовать одному метру в реальном мире. Такой масштаб позволит вам точно отобразить все размеры и пропорции комнаты на листе бумаги.

Пример 2:

Представьте, что у вас есть карта города. Чтобы увидеть все детали и дороги на карте, вы решаете использовать масштаб 1 см – 1 километр. То есть каждый сантиметр на карте будет соответствовать одному километру в реальном мире. Такой масштаб позволит вам легко ориентироваться на карте и планировать маршруты.

Пример 3:

Представьте, что вы изучаете график температур в течение недели. Чтобы лучше увидеть изменения температуры, вы решаете использовать масштаб 1 см – 5 градусов Цельсия. Такой масштаб позволит вам точно отобразить все колебания температуры на графике и увидеть, когда были самые высокие и низкие значения.

Таким образом, использование масштаба в математике помогает нам отображать объекты и данные в масштабе, который позволяет нам увидеть все детали и пропорции. Это очень полезный инструмент в различных областях, таких как строительство, картография и анализ данных.

Различные виды масштаба и их применение

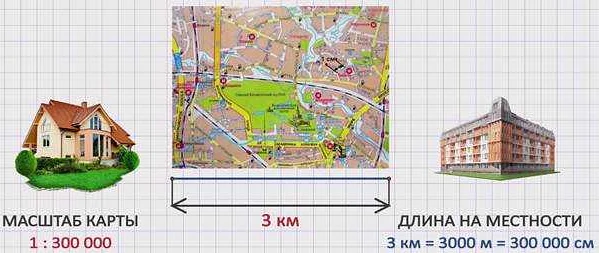
В математике существует несколько видов масштаба, которые применяются для изменения размеров объектов или величин. Каждый вид масштаба имеет свои особенности и применение.

Линейный масштаб используется для изменения размеров фигур или изображений пропорционально. Линейный масштаб задается числом, которое указывает, во сколько раз нужно увеличить или уменьшить размер объекта. Например, если линейный масштаб равен 2, то все размеры объекта увеличиваются в два раза.

Плановый масштаб применяется для изменения размеров планов, карт или схем. Плановый масштаб показывает, во сколько раз уменьшена или увеличена действительная величина на плане. Например, если плановый масштаб равен 1:100, то каждый сантиметр на плане соответствует 100 сантиметрам в реальности.

Временной масштаб используется для изменения временных интервалов. Временной масштаб задает, во сколько раз увеличена или уменьшена продолжительность события или процесса. Например, если временной масштаб равен 1:10, то одна минута на графике соответствует 10 минутам в реальности.

Географический масштаб применяется для изменения размеров местности на карте. Географический масштаб показывает, во сколько раз уменьшена или увеличена действительная площадь на карте. Например, если географический масштаб равен 1:1 000 000, то один сантиметр на карте соответствует одному километру в реальности.

Масштаб регулировки используется для изменения размеров предметов в строительстве или производстве. Масштаб регулировки показывает, во сколько раз нужно изменить размер предмета. Например, если масштаб регулировки равен 1:5, то каждый размер предмета нужно уменьшить в пять раз.

Знание различных видов масштаба поможет вам правильно изменять размеры объектов или величин в математике и других областях жизни.

Как измерить и сравнить масштабы

Чтобы сравнить масштабы двух объектов, нужно измерить их длины с помощью линейки и сравнить полученные значения. Если один объект имеет большую длину, то он будет иметь больший масштаб.

Также можно использовать сравнение отношений. Например, если у нас есть два рисунка, мы можем сравнить длины отрезков на этих рисунках. Если отрезок на одном рисунке в два раза длиннее, чем на другом, то масштаб данного отрезка на первом рисунке будет в два раза больше. Этот метод позволяет сравнивать масштабы объектов, не измеряя их длину.

Используя эти методы, можно измерить и сравнить масштабы различных объектов и установить, какой из них имеет больший или меньший масштаб.

Ошибки при работе с масштабом и как их избежать

При работе с масштабом в математике 4 класса, могут возникнуть определенные ошибки. Важно знать эти ошибки и уметь их избегать, чтобы правильно решать задачи и понимать понятие масштаба.

Одна из распространенных ошибок — неправильное выбор масштаба. Некоторые учащиеся могут выбирать слишком большой или слишком маленький масштаб, что может привести к неправильному решению задачи. Чтобы избежать этой ошибки, необходимо внимательно читать условие задачи и адекватно оценивать размеры предметов или объектов, с которыми работаете.

Другая распространенная ошибка — неправильное использование масштаба. Некоторые учащиеся могут неправильно применять масштаб при измерении или рисовании фигур. Например, они могут ошибочно увеличивать или уменьшать размеры объектов. Чтобы избежать этой ошибки, необходимо внимательно следить за масштабом при работе с измерительными приборами или при рисовании геометрических фигур.

Также, ошибкой может быть неправильное сопоставление значений на шкале. Некоторые учащиеся могут не правильно определять соответствие между значениями на шкале и реальными размерами предметов или объектов. Например, они могут неправильно определить, на какую единицу шкалы соответствует определенное значение размера. Чтобы избежать этой ошибки, необходимо внимательно читать значения на шкале и правильно их интерпретировать.

ОшибкаКак избежать

Неправильный выбор масштаба	Внимательно читать условие задачи и адекватно оценивать размеры предметов или объектов
Неправильное использование масштаба	Внимательно следить за масштабом при работе с измерительными приборами или при рисовании геометрических фигур
Неправильное сопоставление значений на шкале	Внимательно читать значения на шкале и правильно их интерпретировать

Избегая этих ошибок, вы сможете более точно работать с масштабом и правильно решать задачи, связанные с его использованием.

Масштаб в реальной жизни: применение в картографии и строительстве

В картографии масштаб играет решающую роль. Он позволяет определить соотношение размеров на карте и реального мира. Например, если на карте указан масштаб 1:10000, это означает, что каждый сантиметр на карте соответствует 10000 сантиметрам в реальности. Благодаря масштабу, мы можем получить представление о размерах объектов и расстояниях между ними, а также планировать путешествия и ориентироваться на местности.

В строительстве масштаб также играет важную роль. Он позволяет определить соотношение между размерами модели и реального объекта, который будет построен. Например, при проектировании здания на чертеже может быть указан масштаб 1:100. Это означает, что каждый сантиметр на чертеже соответствует 100 сантиметрам в реальности. Благодаря масштабу, строители могут точно воспроизвести размеры и формы здания, а также смоделировать пространство внутри.

В обеих областях масштаб играет важную роль в создании точных и понятных представлений о реальных объектах и местности. Знание и понимание масштаба позволяет нам более эффективно работать с картами, чертежами и моделями, а также лучше понимать и воспринимать окружающий мир.

Вопрос-ответ:

Что такое масштаб в математике?

Масштаб в математике — это соотношение между длинами предметов на рисунке и их длинами в реальной жизни. Он позволяет уменьшить или увеличить изображение в определенное число раз, чтобы оно поместилось на листе бумаги или на экране компьютера.

Зачем нужен масштаб в математике?

Масштаб в математике нужен для того, чтобы создать пропорциональное изображение объектов. С его помощью можно уменьшить или увеличить рисунок, чтобы он вместился на листе бумаги или на экране компьютера. Также масштаб используется для измерения длин предметов на рисунке и в реальной жизни.

Как посчитать масштаб?

Чтобы посчитать масштаб, нужно знать длину предмета на рисунке и его длину в реальной жизни. Затем эти два значения нужно сравнить и выразить их отношение. Например, если предмет на рисунке длиннее в два раза, чем в реальной жизни, то масштаб будет равен 1:2.

Как использовать масштаб на практике?

Масштаб можно использовать на практике, когда нужно уменьшить или увеличить размеры рисунка. Например, если нужно нарисовать карту, то можно использовать масштаб, чтобы изобразить большую территорию на маленьком листе бумаги. Также масштаб используется для измерения длин предметов на рисунке и в реальной жизни.

Можно ли использовать масштаб для измерения площадей?

Нет, масштаб не используется для измерения площадей. Он используется только для измерения длин предметов на рисунке и в реальной жизни. Для измерения площадей нужно использовать другие математические инструменты, такие как формулы или геометрические фигуры.

Что такое масштаб в математике?

Масштаб в математике — это соотношение между размерами предметов на рисунке или плане и их реальными размерами. Он позволяет уменьшить или увеличить изображение, сохраняя пропорции.