Что называют масштабом в математике

Масштаб в математике – это соотношение между величиной объекта или явления в реальном мире и его изображением на плоскости или в пространстве. Узнайте, как определить масштаб и применять его в различных математических задачах.

Масштаб является одним из фундаментальных понятий в математике, которое широко применяется не только в этой науке, но и в различных областях жизни. Он позволяет устанавливать соотношение между объектами, определять их размеры, а также отображать их в различных масштабах.

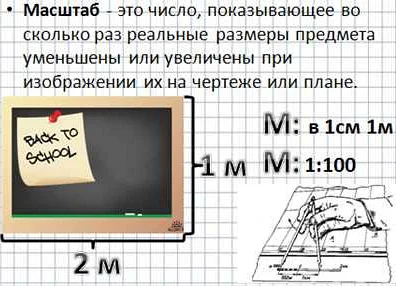
В математике масштаб может быть представлен числом или отношением, которое указывает, насколько уменьшены или увеличены изображаемые объекты по сравнению с реальными. Например, если на карте масштаб составляет 1:1000, то каждый сантиметр на карте соответствует 10 метрам в реальности.

Примеры использования масштаба можно найти в различных областях. В архитектуре он позволяет строить макеты зданий и сооружений, отображая их в определенном масштабе. В картинах и фотографиях масштаб используется для создания перспективы и глубины. В технических чертежах масштаб помогает точно передать размеры и пропорции объектов.

Масштаб в математике – это мощный инструмент, который позволяет наглядно представлять и анализировать объекты и явления в различных масштабах. Он открывает новые возможности для изучения мира и применения математических знаний в повседневной жизни.

Определение масштаба в математике

Масштаб в математике позволяет нам установить соответствие между реальными объектами и их представлениями на бумаге, экране или в моделях. Он играет важную роль в геометрии, картографии, физике и других областях, где требуется точное изображение или моделирование объектов.

Масштаб может быть выражен числом или в виде соотношения между двумя величинами. Например, масштаб карты 1:1000 означает, что одна единица на карте соответствует 1000 единиц в реальном мире. Такой масштаб позволяет нам измерять расстояния на карте и получать представление о фактическом размере объектов.

Масштаб можно применять не только к двумерным объектам, но и к трехмерным моделям. Например, масштаб 1:10 для модели здания означает, что каждый сантиметр на модели соответствует 10 сантиметрам в реальном здании.

Знание масштаба позволяет нам сравнивать объекты, измерять расстояния и размеры, а также создавать точные модели или изображения. Определение масштаба в математике является важным инструментом для работы с геометрическими и физическими объектами, а также для создания и анализа карт и моделей.

Значение масштаба в геометрии

Масштаб используется для установления соответствия между реальными размерами объектов и их изображениями на плоскости. Он позволяет создавать масштабные модели и карты, которые отображают объекты и их размеры в сжатом или увеличенном виде.

Масштаб в геометрии обычно выражается в виде отношения, например 1:100, где первое число указывает длину изображения объекта на плоскости, а второе число – его фактический размер.

Знание масштаба позволяет сравнивать размеры различных объектов и определять расстояния между ними на карте или плане. Оно также помогает в решении задач, связанных с конструкцией и измерением геометрических фигур.

Например, при построении дома на чертеже архитектор использует масштаб, чтобы определить размеры каждой комнаты и расположение мебели. При создании карты города масштаб позволяет определить расстояние между улицами и размеры зданий.

Таким образом, масштаб в геометрии является важным инструментом, который позволяет представить объекты и их размеры на плоскости, сохраняя пропорциональность и соответствие с реальными объектами.

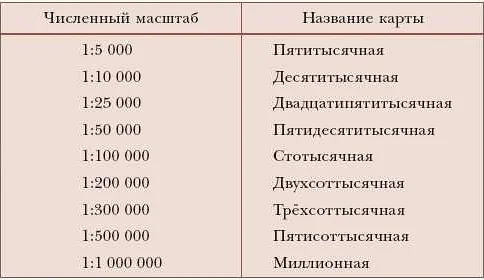
Примеры применения масштаба в картографии

ПримерОписание

1:10 000	Этот масштаб означает, что 1 сантиметр на карте соответствует 10 000 сантиметрам в реальности. Такой масштаб обычно используется для подробных планов городов или зданий.
1:100 000	В этом случае 1 сантиметр на карте соответствует 100 000 сантиметрам в реальности. Такой масштаб применяется, например, при изображении целых территорий или регионов.
1:1 000 000	Для этого масштаба 1 сантиметр на карте соответствует 1 000 000 сантиметрам в реальности. Такой масштаб может использоваться при создании карт мира или континентов.

Масштаб играет важную роль в картографии, поскольку он позволяет представить пространственные объекты на плоскости карты с учетом их реальных размеров. В зависимости от целей и задач картографии, выбирается соответствующий масштаб, который позволяет достичь необходимой степени детализации и точности изображения.

Роль масштаба в графиках и диаграммах

Масштаб играет важную роль в создании и интерпретации графиков и диаграмм. Он определяет отношение между размерами представляемых данных и их отображением на оси координат. Правильное использование масштаба позволяет наглядно представить информацию и сделать выводы на основе визуального представления данных.

При построении графиков и диаграмм необходимо выбирать масштаб таким образом, чтобы все данные были видны и читаемы. Слишком маленький масштаб может сделать график неразборчивым, а слишком большой масштаб может занижать различия между значениями. Поэтому важно подобрать оптимальный масштаб, который подчеркнет важные особенности данных и поможет увидеть закономерности, тренды и выбросы.

Масштаб в графиках и диаграммах может быть линейным или логарифмическим. Линейный масштаб используется, когда значения на оси координат изменяются пропорционально. Например, на графике с линейным масштабом каждый делитель на оси может представлять единицу измерения. Логарифмический масштаб используется, когда значения на оси имеют экспоненциальный характер. На графике с логарифмическим масштабом делители на оси увеличиваются в геометрической прогрессии.

Масштаб также может быть использован для сравнения различных графиков и диаграмм. При сравнении нескольких графиков важно, чтобы они имели одинаковый масштаб, чтобы было легче видеть различия и сходства между ними. Это особенно важно при анализе трендов и изменений во времени или при сравнении различных групп данных.

Корректное использование масштаба в графиках и диаграммах позволяет представить сложные данные в понятной и наглядной форме. Это помогает сделать выводы, выявить закономерности и принять информированные решения на основе представленных данных.

Применение масштаба в пропорциях и подобии

Пропорция – это соответствие между двумя или более величинами, которое подчиняется правилу, что их отношения равно или постоянно. Пропорция выражается в виде отношения двух дробей: a/b = c/d, где a и c это одинаковые величины, также как и b и d.

Когда пропорция соблюдается, можно использовать масштабирование для определения неизвестных величин. Масштабирование подразумевает изменение размера объекта или величин на определенное число раз. Например, если у нас есть пропорция 2/3 = x/9, мы можем использовать масштабирование, чтобы найти значение x. Умножим обе части пропорции на 9, и получим 2/3 * 9 = x. Результатом будет x = 6.

Подобие – это отношение между двумя фигурами, которое говорит о том, что они имеют одинаковую форму, но разный размер. Фигуры подобны, если все их углы равны, а соотношение длин сторон постоянно. Подобие также использует масштабирование для сравнения размеров фигур. Например, если у нас есть два треугольника, один со сторонами 2, 3 и 4, а другой со сторонами 4, 6 и 8, мы можем сказать, что эти треугольники подобны. При этом мы можем использовать масштабирование, чтобы сравнить их размеры. Для этого мы можем разделить длины соответствующих сторон одного треугольника на длины соответствующих сторон другого треугольника и получить постоянное значение.

Таким образом, масштаб является важным инструментом в математике, позволяющим определить соотношения и размеры объектов в пропорциях и подобии.

Масштаб в задачах на расстояния и времена

Одной из часто встречающихся задач на масштаб является задача о времени. Например, предположим, что на графике представлено движение поезда. Ось x соответствует времени, а ось y – расстоянию, пройденному поездом. По графику можно определить, сколько времени поезд затратил на определенное расстояние.

Для решения таких задач необходимо знать масштаб, то есть соотношение между единицой измерения на графике и реальной единицей измерения. Например, если на оси x одна единица соответствует 10 минутам, а на оси y одна единица соответствует 100 километрам, то масштаб составляет 10 минут на 100 километров.

Для решения задач на масштаб необходимо выделить на графике или схеме известные величины и использовать их для определения неизвестной величины. Например, если по графику известно, что поезд затратил 40 минут на преодоление 200 километров, то можно использовать масштаб для определения времени, затраченного на другое расстояние.

Расстояние (в км)Время (в минутах)

100	20
200	40
300	60

Используя таблицу с данными и масштаб, можно определить, сколько времени потребуется на преодоление других расстояний. Например, для расстояния в 150 километров можно использовать пропорцию:

40 минут – 200 километров

x минут – 150 километров

Решив пропорцию, можно определить, что на преодоление расстояния в 150 километров потребуется 30 минут.

Таким образом, масштаб позволяет использовать графики и схемы для решения задач на расстояния и времена, устанавливая соотношение между реальными величинами и их изображениями.

Использование масштаба в задачах с единицами измерения

Масштаб может быть выражен числом или в виде отношения. Например, масштаб 1:100 означает, что каждый сантиметр на чертеже соответствует 100 сантиметрам в реальности.

В задачах с единицами измерения масштаб используется для преобразования значений между различными единицами измерения. Например, если мы знаем, что масштаб между двумя величинами равен 1:10, то мы можем легко определить, что 5 сантиметров на чертеже соответствуют 50 сантиметрам в реальности.

Масштаб также позволяет сравнивать разные объекты и определять их размеры относительно друг друга. Например, если на чертеже масштаб равен 1:50, то мы можем увидеть, что машина, изображенная на чертеже, будет в 50 раз меньше реальной машины.

Использование масштаба в задачах с единицами измерения упрощает работу с большими числами и позволяет легко визуализировать соотношения между объектами. Он широко применяется в архитектуре, строительстве и других областях, где точность и соответствие масштабу являются важными критериями.

МасштабРазмер на чертежеРазмер в реальности

1:100	1 см	100 см
1:50	2 см	100 см
1:10	10 см	100 см

Вопрос-ответ:

Как можно определить масштаб в математике?

Масштаб в математике определяется как соотношение между реальными размерами объекта и их изображением на плоскости. Обычно масштаб выражается в виде отношения длин двух отрезков, причем одна из длин измеряется на плоскости, а другая — в реальном мире.

В каких областях математики используется понятие масштаба?

Понятие масштаба используется в различных областях математики, таких как геометрия, топология, физика и экономика. В геометрии, например, масштаб используется для измерения и сравнения размеров геометрических фигур. В экономике масштаб используется для изучения экономических процессов и прогнозирования их развития.

Как можно применить понятие масштаба в повседневной жизни?

Понятие масштаба можно применить в повседневной жизни для решения различных задач. Например, при покупке мебели можно использовать масштаб для определения того, какой размер мебели будет соответствовать размерам комнаты. Также масштаб можно использовать для измерения расстояний на картах или схемах, чтобы определить, сколько времени займет путь.

Какие примеры использования масштаба в геометрии?

Один из примеров использования масштаба в геометрии — это построение карты или плана города. На карте используется масштаб, чтобы показать соотношение между реальными размерами улиц и зданий и их изображениями на карте. Еще один пример — изображение геометрических фигур на листе бумаги. Здесь масштаб используется для сохранения пропорций и соотношений между сторонами фигуры.

Можно ли использовать масштаб для измерения времени?

Масштаб в математике обычно используется для измерения физических размеров и расстояний, а не времени. Для измерения времени используются другие единицы измерения, такие как секунды, минуты и часы. Однако в некоторых случаях можно использовать масштаб для сравнения длительности различных периодов времени. Например, можно использовать масштаб для сравнения скорости движения разных объектов или для определения, сколько времени займет выполнение определенной задачи.

Что такое масштаб в математике?

Масштаб в математике — это соотношение между размерами объектов на реальном объекте и их изображением на плоскости. Он позволяет установить соответствие между единицами длины на реальном объекте и единицами длины на его изображении.

Как использовать масштабы в математике?

Масштабы могут использоваться в различных областях математики. Например, в геометрии масштаб может использоваться для построения карты или плана. В алгебре масштаб может применяться для установления соотношений между величинами. В общем смысле, масштаб позволяет сравнивать и относить одни величины к другим, устанавливая между ними соответствие.

Практическое применение масштаба в архитектуре и дизайне

В архитектуре масштаб используется для создания планов зданий, фасадов и различных конструкций. Например, архитекторы могут использовать масштаб 1:100, где каждый сантиметр на плане соответствует одному метру в реальности. Это позволяет архитекторам точно представить размеры здания и расположение его элементов, таких как окна, двери и балконы.

В дизайне масштаб также является важным инструментом для создания гармоничных и пропорциональных композиций. Например, при проектировании мебели дизайнеры могут использовать масштаб, чтобы определить размеры каждого элемента и его соотношение с остальными. Это позволяет создать мебель, которая идеально вписывается в интерьер и обеспечивает комфортное использование.

Кроме того, масштаб также применяется при проектировании ландшафтов. Ландшафтные архитекторы могут использовать масштаб для создания планов садов и парков, определяя размеры деревьев, цветников и других элементов. Это позволяет им создавать гармоничные композиции, где каждый элемент соответствует своему месту и пропорциям.

Таким образом, масштаб имеет практическое применение в архитектуре и дизайне, позволяя создавать точные планы и композиции, которые соответствуют реальному масштабу объектов.

Видео по теме: