Что такое масштаб в математике 6 класс определение

Масштаб в математике 6 класс определение. Узнайте, что такое масштаб и как его определять в математике для учеников 6 класса. Понимание масштаба является важным навыком при работе с графиками и картами.

Масштаб – одно из основных понятий в математике, которое широко используется в различных областях науки. В школьном курсе математики масштаб является одной из первых тем, с которой сталкиваются учащиеся начальных классов. Это важное понятие помогает понять, как измерять и сравнивать объекты и явления в окружающем мире.

Масштаб – это соотношение размеров объекта на изображении или на плане к его размерам в реальности. Он выражается числом или дробью и показывает, во сколько раз уменьшены или увеличены размеры объекта. Масштаб может быть представлен в виде дроби, например, 1:100 или 1/100, где первое число обозначает размер объекта на изображении, а второе – его реальный размер.

Пример: Представим, что на плане города масштабом 1:5000 длина улицы равна 6 см. Это означает, что в реальности длина улицы составляет 5000 * 6 = 30000 см или 300 метров.

Масштаб позволяет нам легко сравнивать объекты и явления, которые имеют разные размеры. Он активно используется в географии, архитектуре, топографии и других областях, где важно правильно отобразить объекты на карте или плане. Умение работать с масштабом помогает развивать визуальное мышление и логическое мышление, а также критическое и аналитическое мышление учащихся.

Что такое масштаб в математике

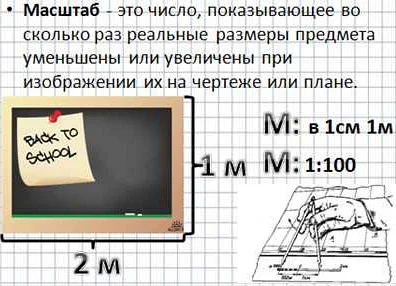
В математике масштаб используется для изменения размеров графиков, диаграмм и других визуальных представлений. Он позволяет отобразить большие числа или промежутки на графике с помощью более удобных и меньших чисел.

Масштаб обычно задается в виде отношения или коэффициента. Например, масштаб 1:100 означает, что каждый единичный отрезок на графике соответствует 100 единицам в реальности.

Если масштаб больше 1, то график или изображение будет увеличено. Если масштаб меньше 1, то график или изображение будет уменьшено.

Масштаб позволяет наглядно представить информацию и упрощает визуализацию и анализ данных. Например, с помощью масштаба можно увидеть мельчайшие детали в графике или сравнить различные данные на диаграмме.

В математике учатся работать с масштабом, чтобы уметь адаптировать графики и диаграммы для удобного представления информации и лучшего понимания математических концепций.

Видео по теме:

Определение масштаба в математике

Масштаб обычно выражается в виде дроби, где числитель представляет длину на изображении, а знаменатель — соответствующую длину в реальности. Например, масштаб 1:100 означает, что каждый сантиметр на изображении соответствует 100 сантиметрам в реальности.

Масштаб широко используется в географии, архитектуре, инженерии и других областях, где важно точно передать соотношение размеров объектов на плане или карте. Он позволяет удобно представить информацию о расположении и форме объектов без необходимости изображать их в реальную величину.

Знание масштаба позволяет легко переводить измерения с плана на реальные размеры и наоборот. Например, зная масштаб плана здания, можно легко определить его реальные размеры, а зная реальные размеры объекта, можно определить его размеры на плане.

Важно помнить, что масштаб не меняет форму объектов, а только их размеры. Поэтому, при использовании масштаба необходимо сохранять пропорции между объектами для достоверного отображения предметов на плане или карте.

Как определить масштаб

Для определения масштаба необходимо знать реальную длину отрезка и его длину на картине.

Для того чтобы определить масштаб, можно использовать следующую формулу:

масштаб = длина на картине / реальная длина

Например, если на карте длина отрезка составляет 5 см, а его реальная длина — 20 км, то масштаб будет:

масштаб = 5 см / 20 км = 1:400 000

Таким образом, масштаб карты будет 1:400 000, что означает, что каждый сантиметр на карте соответствует 400 000 сантиметрам в реальном мире.

Вопрос-ответ:

Что такое масштаб в математике?

Масштаб в математике — это соотношение между длиной отрезка на рисунке и длиной соответствующего отрезка в реальном мире. Он позволяет сократить или увеличить изображение с сохранением пропорций.

Как определить масштаб?

Чтобы определить масштаб, необходимо измерить длину отрезка на рисунке и соответствующий ему отрезок в реальности. Затем, длину отрезка на рисунке нужно разделить на длину соответствующего отрезка в реальности. Полученное число и будет масштабом.

Зачем нужен масштаб в математике?

Масштаб в математике используется для упрощения изображений и карт. Он позволяет уменьшать или увеличивать их размеры, чтобы поместить их на более удобной для анализа поверхности или в более удобном масштабе.

Как использовать масштаб на практике?

Применение масштаба на практике заключается в пропорциональном увеличении или уменьшении размеров объектов. Например, при построении карты города масштаб позволяет изобразить большие расстояния на маленьком листе бумаги. Кроме того, масштаб используется при создании моделей зданий или в расчетах на строительных планах.

В каких областях науки используется масштаб?

Масштаб используется во многих областях науки, таких как география, астрономия, физика, биология и архитектура. Без применения масштаба было бы сложно изучать и анализировать разные объекты и явления в реальных масштабах.

Что такое масштаб в математике?

Масштаб в математике — это соотношение между длинами на модели и соответствующими им длинами в реальном мире.

Примеры использования масштаба

Масштаб может быть использован в различных ситуациях, где необходимо привести объекты или явления к удобному для изучения или представления масштабу. Рассмотрим несколько примеров применения масштаба:

1. Изображение карты

   При создании карты географической области, масштаб используется для установления соотношения между размерами объектов на карте и их реальными размерами на местности. Например, масштаб 1:100000 означает, что каждый сантиметр на карте соответствует 1 километру в реальности.

2. Построение моделей

   При создании моделей, масштаб используется для уменьшения или увеличения размеров объектов для удобства изучения или представления. Например, при создании модели здания в масштабе 1:100, каждый сантиметр на модели соответствует 100 сантиметрам в реальном здании.

3. Графики и диаграммы

   Масштаб используется для представления данных на графиках и диаграммах. Например, на графике температуры за месяц, масштаб может быть использован для установления соотношения между значениями температуры и их отображением на графике.

Это только несколько примеров использования масштаба в математике. Масштаб позволяет нам лучше понимать и представлять различные объекты и явления в удобном для нас формате.

Масштаб на карте

Масштаб на карте обычно выражается в виде дроби или числового значения. Например, масштаб 1:100 000 означает, что 1 сантиметр на карте соответствует 100 000 сантиметрам (или 1 километру) в реальности. Если на карте указано расстояние в 5 сантиметров, то в реальности это будет 5 * 100 000 = 500 000 сантиметров (или 5 километров).

Масштаб на карте позволяет определить длину, ширину, площадь и другие характеристики объектов. Например, если на карте есть прямоугольник, размеры которого в действительности составляют 2 километра по длине и 1 километр по ширине, то по масштабу 1:100 000 его размеры на карте будут составлять 2 * 100 000 = 200 000 сантиметров по длине и 1 * 100 000 = 100 000 сантиметров по ширине.

МасштабОписание

1:10 000	1 сантиметр на карте соответствует 10 000 сантиметрам в реальности
1:50 000	1 сантиметр на карте соответствует 50 000 сантиметрам в реальности
1:100 000	1 сантиметр на карте соответствует 100 000 сантиметрам в реальности
1:1 000 000	1 сантиметр на карте соответствует 1 000 000 сантиметрам в реальности

Точный масштаб на карте очень важен для определения расстояний и характеристик объектов. При использовании карты с неверным масштабом можно получить неправильные результаты и совершить ошибки в ориентации на местности.

Масштаб в графиках

Масштаб может быть разным в разных графиках и определяется в зависимости от рассматриваемых данных. Например, на графике, отображающем изменение температуры в течение дня, масштаб по оси x может быть равномерным и показывать каждый час, а масштаб по оси y может быть разным и показывать изменение температуры в градусах Цельсия.

Определение масштаба в графиках важно для анализа данных и понимания их значений. Он позволяет сравнивать и оценивать величины, находить зависимости и тренды. Например, с помощью масштаба можно определить, насколько быстро растет или уменьшается значение определенной величины.

Примеры масштаба в графиках:

1. График функции: масштаб по оси x может быть равномерным, например, отображать значения с шагом 1, а масштаб по оси y может быть разным, чтобы показать детали изменения функции.
2. Круговая диаграмма: масштаб не имеет значения, так как она отображает соотношение долей или процентов.
3. Столбчатая диаграмма: масштаб по оси x может быть равномерным и показывать категории, а масштаб по оси y может быть разным для отображения величин.

Таким образом, масштаб в графиках помогает нам более полно понимать и анализировать представленную информацию, а также делать выводы и принимать решения на основе полученных данных.

Масштаб в пропорциях

В пропорции масштаб определяется как отношение между длинами соответствующих сторон двух подобных фигур. Например, если у нас есть два треугольника, и их стороны имеют следующие соотношения: 3:6, то масштаб между ними будет 1:2. Это означает, что каждая сторона второго треугольника в два раза больше, чем соответствующая сторона первого треугольника.

Масштаб может быть выражен как десятичная дробь или доля. Например, масштаб 1:2 также может быть записан как 0,5, что означает, что вторая фигура в полтора раза больше первой.

Масштаб часто используется в географии, картографии и архитектуре для создания уменьшенных или увеличенных моделей объектов. Он также играет важную роль в научных исследованиях и инженерных расчетах, где масштабирование объектов и данных может быть необходимым для анализа и прогнозирования.

Задачи на масштаб в математике

Решение задач с использованием масштаба позволяет упростить и наглядно представить сложные математические ситуации. Рассмотрим несколько примеров задач, в которых требуется применить масштаб.

Пример 1:

Ученик нарисовал план комнаты в масштабе 1:50. На чертеже санузел занимает площадь 8 квадратных см. Найдите площадь настоящего санузла в квадратных метрах.

Решение:

Площадь настоящего санузла можно найти, умножив площадь на чертеже на квадрат коэффициента масштаба. В данном случае квадрат коэффициента масштаба равен (1/50)^2 = 1/2500. Поэтому площадь настоящего санузла равна 8 * (1/2500) = 0.0032 квадратных метра.

Пример 2:

На карте расстояние между двумя городами составляет 6 см. Если масштаб карты 1:250000, то какое расстояние в километрах между городами в действительности?

Решение:

Чтобы найти действительное расстояние между городами, нужно умножить расстояние на карте на коэффициент масштаба. В данном случае коэффициент масштаба равен 1/250000. Поэтому действительное расстояние между городами составляет 6 * (1/250000) = 0.000024 км.

Пример 3:

В магазине продается масштабная модель автомобиля в масштабе 1:43. Длина модели равна 12 см. Какова длина настоящего автомобиля в метрах?

Решение:

Чтобы найти длину настоящего автомобиля, нужно умножить длину модели на коэффициент масштаба. В данном случае коэффициент масштаба равен 1/43. Поэтому длина настоящего автомобиля составляет 12 * (1/43) = 0.279 метра.

Задачи на масштаб позволяют применить полученные знания в реальных ситуациях и развить пространственное мышление. Решение таких задач требует внимательности и точности в вычислениях.