Что такое математическая функция определение

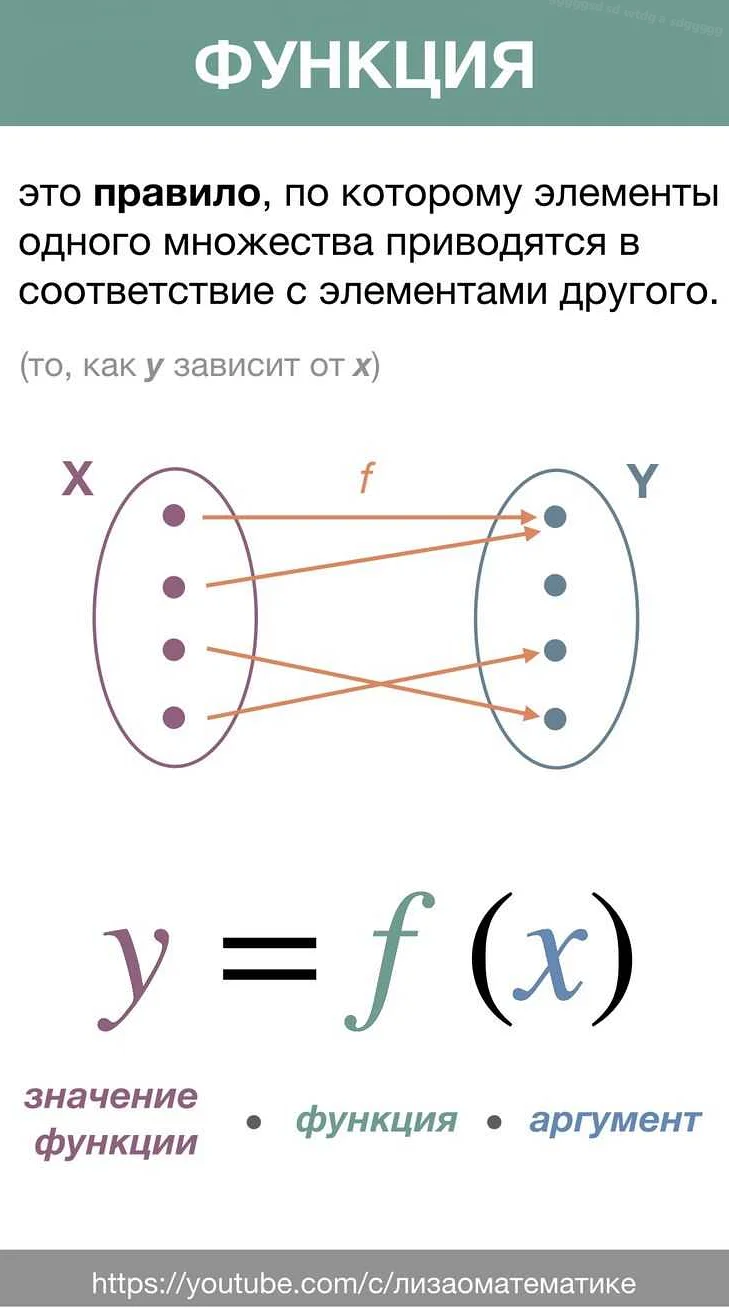
Математическая функция — это математический объект, который сопоставляет элементы из одного множества (называемого областью определения) элементам из другого множества (называемого областью значений) согласно определенному правилу. Узнайте больше о том, что такое математическая функция и как она используется в математике и других областях науки.

Математическая функция — это основное понятие в математике, которое описывает зависимость между двумя множествами чисел. Функция представляет собой правило, согласно которому каждому элементу из одного множества (называемого областью определения) сопоставляется элемент из другого множества (называемого областью значений). Функции часто обозначаются буквами, например, f(x) или g(y).

В математике функции имеют широкое применение и используются для моделирования различных процессов. Они помогают анализировать и понимать различные явления, описывать зависимости между переменными и решать различные задачи. Функции могут быть представлены в виде формул, графиков, таблиц и диаграмм.

Примером математической функции может быть функция y = 2x. Здесь x — это переменная, а 2x — это выражение, зависящее от x. Каждому значению переменной x будет соответствовать значение y, которое будет в два раза больше значения x. Например, если x = 3, то y = 2 * 3 = 6. Таким образом, функция y = 2x описывает зависимость между x и y, где y всегда равно удвоенному значению x.

Математическая функция: определение и примеры

Функция обозначается символом f и записывается в виде f(x), где x — входное значение. Значение f(x) называется образом x при отображении f. Входные значения называются аргументами функции, а значения, полученные в результате вычисления функции, — значениями функции.

Примером математической функции может служить функция f(x) = 2x + 3. В этом примере аргументом функции является x, а выражение 2x + 3 описывает зависимость между аргументом и значением функции. Например, при x = 2, значение функции будет равно 2 * 2 + 3 = 7.

Функции могут иметь различные свойства, такие как область определения, область значений и график. Область определения — это множество всех возможных аргументов функции, а область значений — множество всех значений функции. График функции представляет собой геометрическое представление зависимости между аргументом и значением функции.

Математические функции широко используются в различных областях, таких как физика, экономика, компьютерная наука и др. Они позволяют описывать и моделировать различные явления и процессы и являются основой для решения множества задач.

Примеры математических функцийОписание

f(x) = x^2	Квадратичная функция, значение которой равно квадрату аргумента.
f(x) = sin(x)	Тригонометрическая функция, значение которой равно синусу аргумента.
f(x) = e^x	Экспоненциальная функция, значение которой равно экспоненте в степени аргумента.

Определение математической функции

В математике функция обычно обозначается символом f и определяется доменом (множеством значений, на котором функция определена), и областью значений (множеством, в которое отображаются элементы домена).

Функции могут быть заданы различными способами: алгебраическими формулами, графиками, таблицами и т.д. Примеры функций включают простые арифметические операции, такие как сложение и умножение, и более сложные математические функции, такие как тригонометрические функции и логарифмы.

Функции в математике играют важную роль и используются во многих областях, включая физику, экономику, компьютерные науки и другие дисциплины.

Математическое обозначениеПример

f(x)	f(x) = x^2
g(x)	g(x) = sin(x)
h(x)	h(x) = log(x)

Основные понятия

Область определения — это множество всех возможных входных значений для функции. Она определяет, какие значения можно подать на вход функции.

Область значений — это множество всех возможных выходных значений для функции. Она определяет, какие значения могут быть возвращены функцией.

Функция обычно обозначается символом f, за которым следует аргумент в круглых скобках. Например, f(x).

Аргумент — это значение, подаваемое на вход функции. Он может быть любым элементом из области определения.

Значение функции — это результат работы функции для конкретного аргумента. Оно является элементом из области значений.

График функции — это визуальное представление функции на плоскости. Он показывает, как значения функции меняются в зависимости от значения аргумента.

Примеры математических функций: f(x) = x^2, f(x) = sin(x), f(x) = 2x + 3. В этих примерах x — аргументы функции, а x^2, sin(x), 2x + 3 — значения функции для соответствующих аргументов.

Примеры математических функций

В математике существует множество различных типов функций, каждый из которых имеет свои особенности и применения. Рассмотрим некоторые примеры:

1. Линейная функция: y = kx + b. Примером линейной функции может служить функция y = 2x + 3, где k = 2 и b = 3. Эта функция задает прямую на координатной плоскости, где k — угловой коэффициент, определяющий наклон прямой, а b — свободный член, определяющий смещение прямой по оси y.

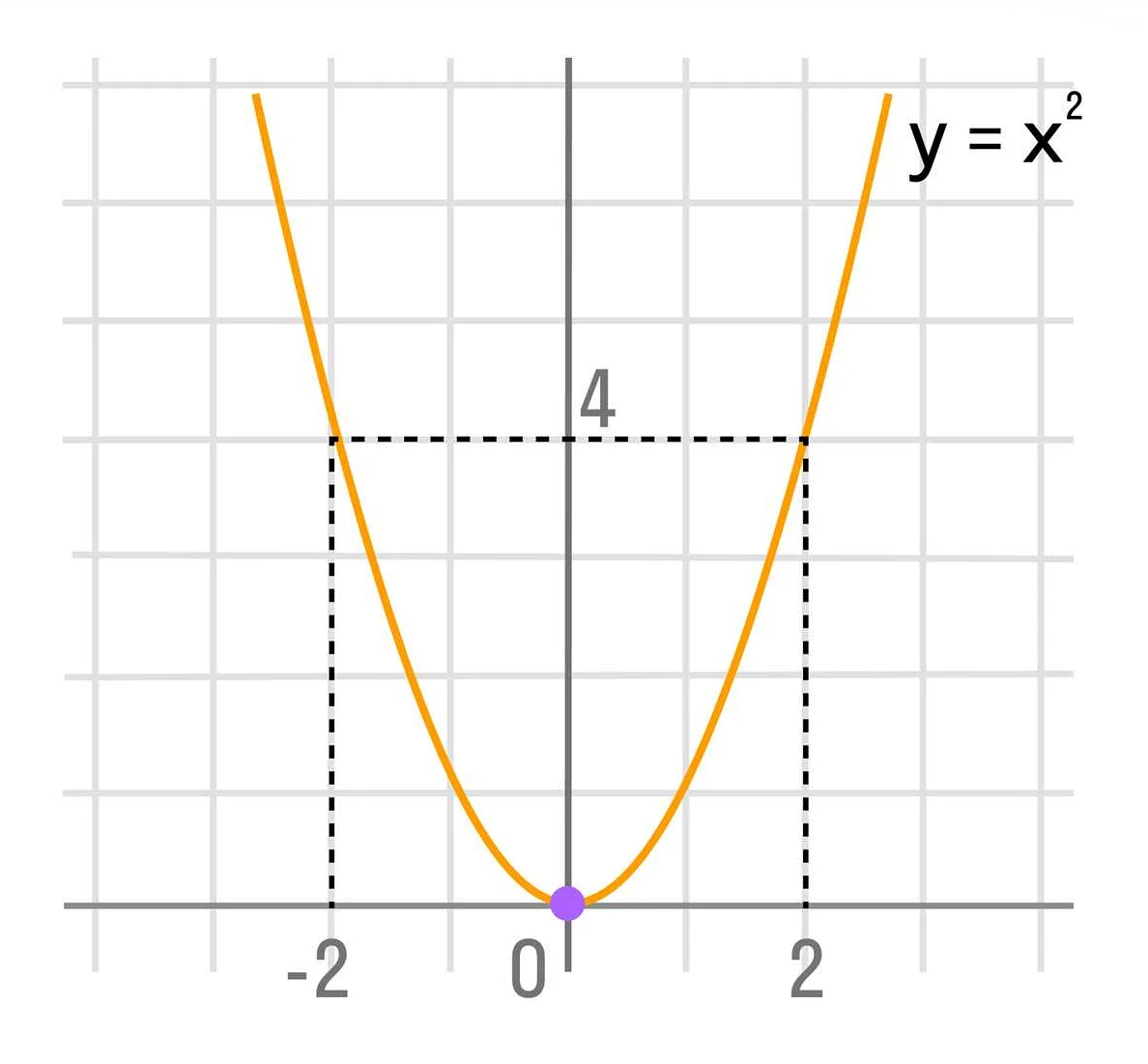
2. Квадратичная функция: y = ax^2 + bx + c. Примером квадратичной функции может служить функция y = x^2 — 2x + 1, где a = 1, b = -2 и c = 1. Эта функция задает параболу на координатной плоскости.

3. Тригонометрическая функция: y = sin(x). Примером тригонометрической функции может служить функция y = sin(x), которая описывает синусоиду.

4. Экспоненциальная функция: y = a^x. Примером экспоненциальной функции может служить функция y = 2^x, где a = 2. Эта функция растет очень быстро при увеличении значения x.

5. Логарифмическая функция: y = log_a(x). Примером логарифмической функции может служить функция y = log_2(x), где a = 2. Эта функция обратна к экспоненциальной функции и показывает, в какую степень нужно возвести основание a, чтобы получить значение x.

Это лишь некоторые примеры математических функций, существует множество других функций, каждая из которых имеет свои уникальные свойства и применения.

Линейная функция

Формула линейной функции имеет вид:

y = kx + b

где k и b – постоянные числа, которые называются коэффициентами линейной функции. Коэффициент k называется коэффициентом наклона, а коэффициент b – свободным членом.

График линейной функции представляет собой прямую линию на координатной плоскости.

Примеры линейных функций:

1. y = 2x + 5 – функция с коэффициентом наклона 2 и свободным членом 5.
2. y = -3x + 2 – функция с коэффициентом наклона -3 и свободным членом 2.
3. y = 0.5x – функция с коэффициентом наклона 0.5 и свободным членом 0.

Квадратичная функция

Коэффициент a влияет на крутизну графика функции. Если a > 0, то график открывается вверх, а если a < 0, то график открывается вниз.

Коэффициенты b и c определяют положение графика функции на координатной плоскости. Коэффициент b отвечает за сдвиг графика влево или вправо, а коэффициент c — за сдвиг вверх или вниз.

Квадратичная функция может иметь различные формы графика: параболу, параболу с ветвями, параболу с дополнительным максимумом или минимумом.

Пример квадратичной функции: f(x) = 2x^2 — 3x + 1

xf(x)

-2	15
-1	6
0	1
1	0
2	3

Степенная функция

Степенная функция может иметь различные значения n, которые могут быть как положительными, так и отрицательными. Если n — целое число, то степенная функция может быть представлена в виде многочлена.

Например, f(x) = x^2 — это квадратичная функция, f(x) = x^3 — это кубическая функция, f(x) = x^0 — это константная функция, f(x) = x^(-1) — это функция с отрицательной степенью, которая может быть представлена как обратная функция f(x) = 1/x.

Степенная функция может иметь различные графики в зависимости от значения степени. Например, когда n — четное число, график степенной функции будет иметь форму параболы, а когда n — нечетное число, график будет иметь форму «буквы S».

Степенные функции широко используются в математике, физике, экономике и других науках для моделирования реальных процессов и явлений.

Тригонометрическая функция

Одним из самых известных примеров тригонометрической функции является синус (sin). Синус угла определяется отношением противолежащего катета к гипотенузе прямоугольного треугольника. Значение синуса может принимать значения от -1 до 1.

Еще одной тригонометрической функцией является косинус (cos). Косинус угла определяется отношением прилежащего катета к гипотенузе прямоугольного треугольника. Значение косинуса также может принимать значения от -1 до 1.

Тангенс (tan) — это отношение синуса косинусу, то есть противолежащего катета к прилежащему. Значение тангенса может быть любым рациональным числом.

Также существуют обратные тригонометрические функции, такие как арксинус (asin), арккосинус (acos) и арктангенс (atan). Они позволяют находить угол, соответствующий определенному значению синуса, косинуса или тангенса.

Логарифмическая функция

Логарифмическая функция позволяет найти значение показателя степени, при котором основание логарифма нужно возвести, чтобы получить заданное число. Например, для функции y = log2(x) значение y будет равно показателю степени, при котором число 2 нужно возвести, чтобы получить число x.

Логарифмическая функция имеет свои особенности, например, она не определена для отрицательных чисел и нуля. Кроме того, при x = 1 значение функции равно 0, так как любое число, возводимое в степень 0, равно 1.

Примеры логарифмической функции:

• y = log10(x) — десятичный логарифм;
• y = ln(x) — натуральный логарифм;
• y = log2(x) — двоичный логарифм.

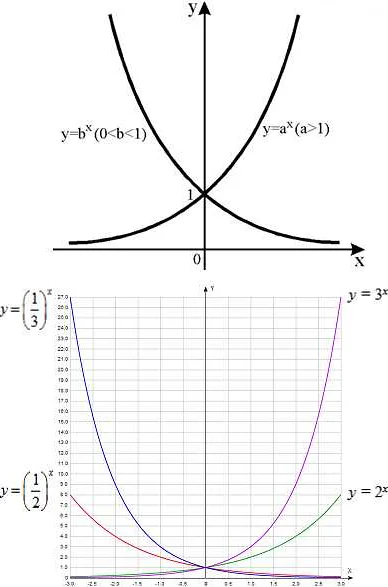
Экспоненциальная функция

Основание экспоненты a может быть любым положительным числом, кроме 1. Когда основание a больше 1, экспоненциальная функция растет экспоненциально, то есть быстро увеличивается с ростом значения переменной x. Когда основание a между 0 и 1, экспоненциальная функция убывает экспоненциально, то есть быстро уменьшается с ростом значения переменной x.

Примерами экспоненциальных функций являются функции f(x) = 2^x и f(x) = (1/2)^x. В первом случае основание экспоненты равно 2, поэтому функция растет с ростом значения x. Во втором случае основание экспоненты равно 1/2, поэтому функция убывает с ростом значения x.

Вопрос-ответ:

Что такое математическая функция?

Математическая функция — это отображение, которое каждому элементу из одного множества ставит в соответствие элемент из другого множества. Она описывает зависимость между двумя переменными и является основным понятием в математическом анализе.

Какие могут быть примеры математических функций?

Примеры математических функций включают линейную функцию, квадратичную функцию, тригонометрические функции (синус, косинус и тангенс), экспоненциальную функцию и логарифмическую функцию.

Как определить, что данное отображение является функцией?

Для того чтобы отображение было функцией, каждому элементу из одного множества должен соответствовать ровно один элемент из другого множества. Если для одного элемента из первого множества существует несколько элементов из второго множества, то это не функция.

Как можно представить математическую функцию графически?

Математическую функцию можно представить графически с помощью графика. Для этого оси координат разбиваются на две части — горизонтальную (ось абсцисс) и вертикальную (ось ординат), и на графике отображается зависимость между значениями переменных.

Чем отличается линейная функция от квадратичной функции?

Линейная функция описывает зависимость между переменными, которая представляется прямой линией на графике. Квадратичная функция описывает зависимость, которая представляется параболой на графике. В линейной функции степень переменной равна 1, а в квадратичной функции — 2.

Видео по теме: