Математическая структура: что это такое и как ее понять

Математическая структура — это абстрактное понятие, описывающее упорядоченный набор математических объектов, связанных между собой определенными законами преобразования. Они могут быть представлены в виде графов, деревьев, групп, кольце и других алгебраических объектов. Понимание принципов математических структур является ключевым для углубленного изучения математики и ее приложений в различных областях науки и техники.

Математическая структура — это набор математических объектов, снабженный определенными операциями и отношениями. Примерами могут служить числа, функции, группы, множества, пространства и другие объекты. Различные математические структуры призваны решать различные задачи и помогают математикам находить новые связи между объектами и выводить новые теоремы.

Одна из важных задач, решаемых при помощи математических структур, — это поиск решений сложных задач. Математики используют различные математические структуры для описания и изучения моделей, которые помогают понимать различные виды явлений, от простых до высоконагруженных и технически сложных вопросов.

Например, математические структуры могут помочь в решении задач физики, которые приблизительно описывают движение объекта или изменение состояния системы. Они также могут использоваться для анализа сложных данных и разработки алгоритмов для обработки информации. Математические структуры находят применение в различных областях науки, таких как биология, социология и экономика.

Математическая структура и ее применение в решении задач

Математическая структура — это набор элементов и операций, которые определяют определенные отношения между этими элементами. Примеры математических структур включают числа, графы, множества, векторы и другие. Они используются для формализации и абстракции реальных проблем и являются мощным инструментом для решения сложных задач.

Применение математических структур позволяет упростить задачи, которые могут быть слишком сложными для решения в реальном мире. Например, графы могут использоваться для моделирования социальных сетей или транспортных систем, а множества могут использоваться для формализации правил и ограничений в логических выражениях. Эти модели могут помочь разработчикам программного обеспечения решить сложные задачи.

Помимо приложений в программировании, математические структуры широко используются в науке, инженерии и других областях. Например, в теории графов используются для моделирования сложных систем, а в теории вероятностей — для предсказания рисков и вероятности событий. Соответственно, знание различных математических структур может помочь нам более эффективно решать различные задачи.

В целом, понимание математических структур необходимо для успешного решения задач в различных дисциплинах и повседневной жизни. Использование этих инструментов позволяет увидеть общую структуру проблемы и решить ее более эффективно.

Видео по теме:

Что такое математическая структура?

Математическая структура — это набор элементов и операций, упорядоченных в соответствии с определенными правилами. Эти правила описывают, какие операции могут быть выполнены над элементами, и какие результаты могут быть получены при их выполнении. В математической структуре каждый элемент имеет определенную роль и значение, и позволяет совершать определенные операции над ними.

Конкретные примеры математических структур включают множества, векторы, графы, алгебры и теории множеств. Математические структуры широко используются в различных областях науки и техники, таких как физика, информатика, экономика и статистика.

Важными свойствами математических структур являются их абстрактность и формальность. Абстрактность означает, что математические структуры описываются в терминах элементов и операций, без отсылок к конкретным явлениям в реальном мире. Формальность означает, что все правила и определения математической структуры являются точными и четкими, определены формальным языком логики.

Почему математическая структура важна в научных и инженерных исследованиях?

Математическая структура является основой для решения сложных научных и инженерных задач. Она позволяет нам представлять информацию в виде конкретных объектов и определять их взаимосвязь.

Например, в геометрии мы можем использовать математические структуры для описания свойств и форм объектов, что позволяет нам построить точные и эффективные модели. В физике мы используем математические структуры для описания физических законов и связей между различными физическими величинами.

Математическая структура также играет ключевую роль в обработке данных. Благодаря ей мы можем анализировать большие объемы данных, определять закономерности и выделять важную информацию. Это особенно важно в научных и инженерных исследованиях, где мы часто имеем дело с огромными объемами информации.

В итоге, математическая структура позволяет нам сделать точные предсказания и принимать эффективные решения в различных областях науки и техники. Без нее наше понимание мира было бы сильно ограничено и мы не могли бы решать многие сложные задачи, с которыми мы сталкиваемся в наших исследованиях.

Какие математические структуры существуют и чем они отличаются друг от друга?

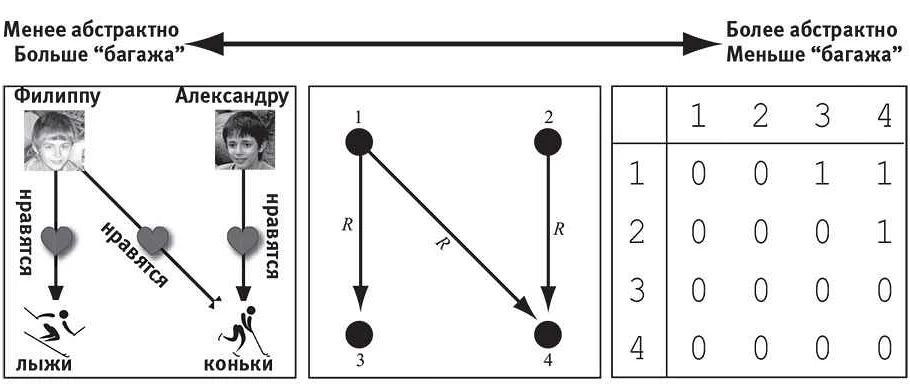
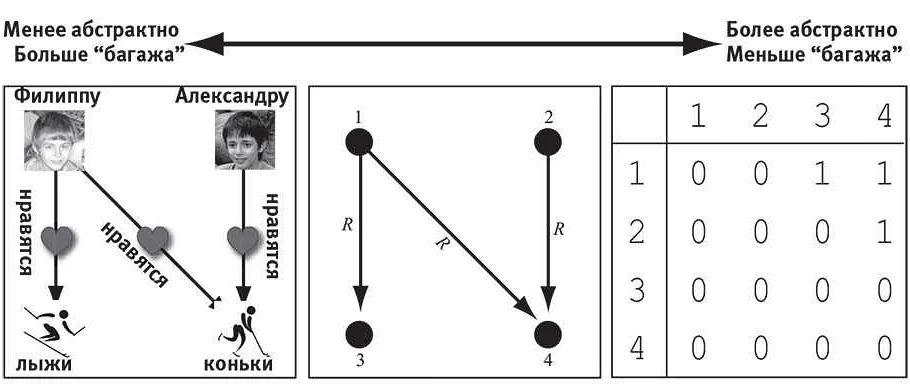
Математические структуры — это абстрактные объекты, которые имеют определенные свойства и отношения между ними. Существует много разных математических структур, каждая из которых решает определенный класс задач. Вот некоторые из них:

• Графы: это структуры, состоящие из вершин и ребер, которые связывают эти вершины. Графы используются для моделирования сетей и связей во многих областях, включая теорию графов и компьютерные науки.
• Векторные пространства: это структуры, состоящие из элементов, которые могут быть складываться и умножаться на скаляры. Векторные пространства используются для моделирования физических систем, таких как движение тел и электромагнетизм. Они также используются в линейной алгебре и геометрии.
• Алгебраические структуры: это структуры, которые имеют операции, которые выполняются над элементами множества. Примеры включают группы, кольца и поля. Алгебраические структуры используются в алгебре и математической физике.
• Последовательности и ряды: это структуры, состоящие из элементов, которые следуют в определенном порядке. Последовательности и ряды используются в анализе, которые изучают свойства функций.

Каждая из этих математических структур имеет свои особенности и применения. Некоторые из них взаимосвязаны и используются вместе, в то время как другие являются независимыми и имеют уникальные приложения.

Как математическая структура помогает в решении задач?

Математическая структура позволяет систематизировать знания и методы математики. Она представляет собой совокупность элементов и отношений между ними, которые с помощью математических операций могут быть описаны и исследованы.

Благодаря математической структуре можно решать задачи на более высоком уровне. Например, задачи, которые представляют собой большие объемы информации и не могут быть решены обычными методами. Или задачи, которые требуют решения сразу нескольких подзадач.

Кроме того, математическая структура помогает обобщать полученные результаты и выводы на другие задачи, что позволяет существенно экономить время и ресурсы при решении новых задач.

Важно отметить, что при использовании математической структуры необходима точность и логическая верность решений. Даже небольшая ошибка может привести к неверным выводам и неправильным решениям.

Итак, математическая структура является мощным инструментом для решения сложных задач, которые не могут быть решены обычными методами. Она позволяет систематизировать знания и методы математики, решать задачи на более высоком уровне и обобщать полученные результаты и выводы на другие задачи. Однако, при использовании математической структуры необходима точность и логическая верность решений.

Как использовать математическую структуру для анализа данных?

Математические структуры могут быть очень полезны при анализе данных, так как они позволяют нам найти закономерности и шаблоны в больших объемах информации. Некоторые из наиболее часто используемых структур включают понятия, такие как графы, деревья и матрицы.

Графы используются для представления связей между объектами. Они могут быть использованы для анализа социальных сетей или маршрутов перемещения в городе. Каждый объект представляется вершиной, а связи между ними — ребрами.

Деревья используются для иерархической организации данных. Например, они могут быть использованы для представления классификаций животных или организации кода программы. Каждый узел представляет категорию, а связи между ними — отношения «родитель-ребенок».

Матрицы используются для представления связей между объектами в числовой форме. В матрице каждому элементу соответствует определенное значение, которое отражает взаимодействие между объектами. Они могут быть использованы для анализа сетей передачи данных или оценки взаимодействия групп в эксперименте.

Использование математических структур для анализа данных позволяет нам получить более точные и четкие результаты, чем простое ручное исследование. Кроме того, это может помочь нам найти новые взаимосвязи между объектами и улучшить наши предсказания будущих событий.

Примеры использования математической структуры в решении задач в разных областях

Математическая структура, в основном, используется для решения сложных задач в разных областях, таких как физика, экономика, компьютерные науки и т.д. В экономике, структуры используются для анализа цен, доходов, инфляции и других факторов, влияющих на финансовые показатели. Это позволяет выделить основные тенденции и делать прогнозы для будущего.

В физике, математические структуры используются для описания физических законов и явлений. Например, для описания движения тела в пространстве и времени, используется математическая структура в виде уравнений Ньютона или уравнений Максвелла для описания электромагнитных явлений.

В компьютерных науках, структуры используются для описания алгоритмов и структур данных. Это позволяет эффективно решать задачи такие как сортировка, поиск данных и решение задач искусственного интеллекта.

Математические структуры также используются в геометрии, алгебре, теории чисел и топологии. Они позволяют абстрагироваться от конкретных объектов, и рассматривать их свойства более общим способом. Например, невозможно построить идеальный круг в реальном мире, однако используя геометрические структуры, можно описать свойства идеального круга.

Где еще можно применять математическую структуру?

Математическая структура широко используется в различных областях науки, техники и искусства. Вот несколько примеров:

1. Физика: математические структуры, такие как векторные поля, теория множеств и дифференциальные уравнения, используются для описания и анализа физических явлений. Например, теория графов применяется в физике для моделирования сложных структур, таких как сети связных частиц.
2. Компьютерные науки: математические структуры используются для представления данных и алгоритмов. Например, графы используются для поиска кратчайшего пути в сетях, а теория множеств применяется для построения баз данных.
3. Музыка: Музыкальные композиции могут быть расценены как математические структуры. Музыкальные ноты могут быть представлены числами, а композиции могут быть описаны и анализированы при помощи математических моделей.
4. Искусственный интеллект: математические структуры используются в машинном обучении и искусственном интеллекте для анализа данных и создания алгоритмов. Например, нейронные сети используются для распознавания образов и решения других задач машинного обучения.
5. Экономика: Математические структуры используются в экономических моделях для прогнозирования будущих трендов и принятия решений. Например, теория игр используется для анализа стратегий компаний, а ряды Фурье используются в финансовых моделях.

Таким образом, математическая структура имеет широкое применение в различных областях науки и техники и играет важную роль в решении различных сложных задач.

Какие проблемы могут возникнуть при применении математической структуры и как их решать?

Если говорить об общих проблемах при применении математической структуры, то можно выделить несколько пунктов.

1. Сложность математических моделей. Во многих случаях ситуация, которую нужно описать с помощью математической модели, может быть очень сложной или недостаточно изученной. Это усложняет задачу создания соответствующей математической структуры. Для решения данной проблемы необходимо тщательно проводить исследования и осуществлять уточнение модели.

2. Недостаточность данных. Для построения математической модели необходимо иметь определенное количество данных. В случае отсутствия или недостаточности данных не получится создать точную модель. Эту проблему можно решать, например, путем проведения дополнительных исследований или использования других методов обработки данных.

3. Сложность вычислений. Во многих случаях математические модели очень сложны, и их вычисление требует больших вычислительных ресурсов. Для решения этой проблемы используются методы оптимизации вычислений и снижения сложности моделей.

4. Необходимость интерпретации результатов. Получаемый результат в большинстве случаев нужно интерпретировать. Эта задача может быть достаточно сложной и требовать специальной подготовки и опыта. Для решения данной проблемы можно использовать дополнительные методы и инструменты анализа данных.

Для решения данных проблем важно использовать современные методы математического моделирования и обработки данных, а также проводить многоуровневое тестирование и уточнение полученных результатов.

Какие факторы влияют на эффективность использования математической структуры в решении задач?

Уровень знаний и навыков математики: Чем выше уровень знаний и навыков математики, тем более эффективно можно использовать математическую структуру для решения сложных задач. Необходимо хорошо знать математические понятия, формулы, методы и приемы, чтобы использовать их правильно.

Качество математических моделей: Результаты применения математической структуры в решении задач сильно зависят от качества математических моделей. Чем точнее и более полно определены параметры модели, тем точнее и более достоверны результаты. Необходимо уметь формулировать математические модели на основе поставленной задачи.

Способность к абстрактному мышлению: Для эффективного использования математической структуры в решении задач необходима способность к абстрактному мышлению. Нужно уметь переносить задачу на более абстрактный уровень, анализировать и находить закономерности, свойства и отношения между объектами.

Компьютерные технологии: Современные компьютерные технологии позволяют эффективно использовать математические структуры в решении сложных задач. Использование специальных программ и алгоритмов позволяет автоматизировать процесс решения задач и получать результаты с большей точностью и скоростью. Необходимо уметь использовать эти технологии и программы.

Как развивается теория математических структур?

Теория математических структур является одной из фундаментальных областей современной математики. Её развитие началось ещё в XIX веке, когда математики стали заниматься абстрактными структурами, не имеющими непосредственного отношения к физическому миру. Уже тогда были выделены такие структуры, как группы, кольца и поля.

В XX веке теория математических структур начала развиваться ещё интенсивнее. Изучение таких структур, как топологические пространства, породило развитие топологии — раздела математики, который изучает геометрические свойства топологических пространств.

В настоящее время теория математических структур продолжает развиваться, порождая новые области математики. К примеру, теория категорий возникла в результате попытки формализации общих понятий в различных областях математики.

При этом развитие теории математических структур не ограничивается только математическими исследованиями. Математические структуры нашли широкое применение в других областях науки и техники, например, в информатике и теоретической физике.

Таким образом, теория математических структур продолжает расти и развиваться, играя невероятно важную роль в различных областях науки и техники.

Вопрос-ответ:

Что такое математическая структура?

Математическая структура — это некоторое множество объектов, снабженное различными операциями, отношениями и свойствами, которые задают порядок и связи между элементами множества. Она позволяет формализовать и описать сложные объекты и явления в математике, физике, экономике, информатике и других науках.

Для чего нужна математическая структура?

Математическая структура помогает описывать сложные объекты и процессы в различных науках, формализовывать и выражать их свойства и отношения, а также решать сложные задачи путем применения различных математических методов и теорий. Она также позволяет упростить и систематизировать информацию для более легкого и точного анализа и прогнозирования.

Какие примеры математических структур существуют?

Существует множество примеров математических структур, например, группы, кольца, поля, множества, топологии, метрики и др. Каждая из них имеет свои свойства, операции и отношения, которые используются в различных областях науки и жизни для решения различных задач.

Как математическая структура помогает в информатике?

Математическая структура помогает описывать и анализировать алгоритмы, структуры данных, программы и др. Общие математические понятия, такие как функции, графы, пространства, множества и др., широко используются в информатике для формализации задач и построения эффективных алгоритмов для их решения.

Как использовать математическую структуру для решения сложных задач в физике?

В физике математическая структура используется для описания различных явлений и процессов, таких как электромагнетизм, термодинамика, квантовая механика и др. Она помогает формализовать и выразить законы и свойства этих процессов, а также разработать математические модели для их анализа и предсказания.

Что такое группа в математической структуре?

Группа — это математическая структура, состоящая из множества элементов и операции, обладающей свойствами ассоциативности, существования нейтрального элемента и обратного элемента для каждого элемента множества. Группы широко используются в математике, физике, информатике и других науках для выражения и изучения различных геометрических, алгебраических и топологических свойств объектов и процессов.

Как математическая структура помогает в экономике?

В экономике математическая структура используется для описания и анализа различных явлений и процессов, таких как производственные функции, модели потребительского поведения, экономические равновесия и др. Она помогает формализовать и выразить законы и отношения в экономике, а также создать математические модели для прогнозирования и оптимизации различных экономических показателей и процессов.