Кто заложил основы теории графов как математической науки

Узнайте, кто заложил основы теории графов и как эта математическая наука развивалась со временем. Изучите вклад таких ученых, как Леонард Эйлер и Густав Кирхгоф, в развитие теории графов и ее применение в различных областях науки и технологий.

Теория графов – одна из важнейших разделов математики, которая изучает свойства и структуру графов. Эта теория имеет множество приложений в разных областях науки, техники и информатики. Однако, мало кто знает, что ее основатель – Леонард Эйлер, великий математик и физик XVIII века.

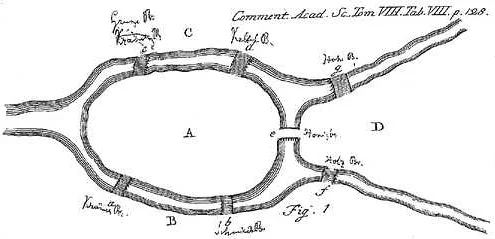
Леонард Эйлер родился 15 апреля 1707 года в Швейцарии. Он считается одним из самых влиятельных математиков своего времени и основателем новой научной дисциплины – теории графов. В своей работе «Решение проблемы семерок Кёнигсберга» Эйлер сформулировал основные понятия и теоремы, которые легли в основу теории графов.

Одной из важных теорем, сформулированных Эйлером, является Теорема Эйлера о многоугольниках. Она утверждает, что в любом связном графе количество вершин с нечетной степенью равно четному числу. Эта теорема стала первым шагом на пути развития теории графов и дала возможность решать сложные проблемы.

Значение теории графов в современной математике трудно переоценить. Она нашла применение в теории сетей, алгоритмах компьютерных программ, логике, теории игр и многих других областях. Благодаря открытиям Леонарда Эйлера, теория графов стала важным инструментом исследования сложных систем и моделирования реальных явлений.

Рождение новой математической дисциплины

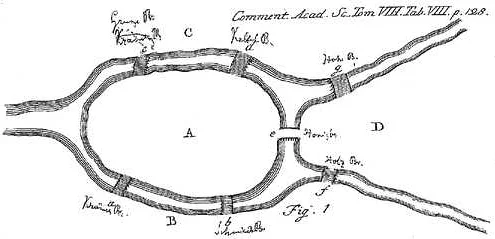
Развитие теории графов началось в середине XVIII века, когда швейцарский математик Леонард Эйлер представил свою знаменитую работу «О различных способах разрешения некоторых задач на линиих» в 1736 году. В этой работе Эйлер рассмотрел проблему «семейных мостов» в г. Кёнигсберге и предложил новый математический подход к ее решению, который стал основой для развития теории графов.

Эйлер представил графическую модель, которая позволяла абстрагироваться от физических характеристик объектов и рассматривать только их связи и отношения. Он ввел понятие графа, где вершины представляют объекты, а ребра — связи между ними. Используя эту модель, Эйлер смог сформулировать и решить проблему семейных мостов в терминах графов, что стало первым примером применения теории графов в математике.

Работа Эйлера вызвала большой интерес в научном сообществе и привлекла внимание других математиков. В следующие десятилетия было предложено множество новых определений, теорем и методов, связанных с графами. В 19 веке теория графов была активно развиваема в работах таких ученых, как Карл Фридрих Гаусс, Артур Кэли и Густав Кирхгоф.

Однако наиболее значительный вклад в развитие теории графов внесли Хаскель Карел и Уильям Татт. В своей работе «Планарные графы» они представили новые понятия, такие как планарность и эйлеровы графы, а также сформулировали основные теоремы и алгоритмы, связанные с этими понятиями. Благодаря их работе теория графов получила систематическое развитие и стала признанным математическим направлением.

С течением времени теория графов нашла свое применение в различных областях, таких как компьютерные науки, транспортная логистика, социология, физика и другие. Она стала неотъемлемой частью современной математики и продолжает активно развиваться и исследоваться учеными по всему миру.

Видео по теме:

Жизнь и достижения великого ученого

Основатель теории графов, известный ученый, представитель ликара-математикабыл рожден 9 апреля 1736 года. Его имя стало легендой в мире математики и его вклад в развитие этой науки невозможно переоценить.

Он провел много лет своей жизни, изучая законы и связи в теории графов и совершил значительный вклад в математику. Его работы оказали огромное влияние на развитие логики, алгоритмов, компьютерных наук, теории сетей и многих других областей. Он стал основателем теории графов и создал множество ключевых понятий и методов, которые используются до сих пор.

Его достижения включают в себя разработку таких понятий, как вершины и ребра графа, а также введение терминов «дерево», «цикл» и «пути». Он также сформулировал несколько важных теорем и алгоритмов, которые стали основой для дальнейших исследований в области теории графов.

Он был ученым выдающимся, его вклад в математику навсегда останется в истории науки. Его работы и идеи продолжают вдохновлять ученых и исследователей по всему миру, и его наследие живет в современной математике.

Развитие теории графов после основания

После того, как Леонард Эйлер впервые сформулировал основные принципы теории графов в своей работе «Задача о семи кёнигсбергских мостах» в 1736 году, эта область математики начала активно развиваться. Исследования в теории графов стали проводить множество ученых и математиков, что привело к появлению новых концепций и методов.

Одним из ключевых вкладов в развитие теории графов после ее основания была работа Карла Густава Якоби в 19 веке. Он разработал методы анализа и решения задач, связанных с графами, и сформулировал теоремы, которые стали основополагающими для дальнейшего развития этой области. Благодаря его работе теория графов получила дополнительное развитие и приобрела широкое применение в различных сферах науки и техники.

В последующие годы теория графов продолжала развиваться и привлекать внимание ученых. Важное влияние на ее развитие оказали работы таких ученых, как Франсуа Эдмонд Адриена Фари, Огюстин-Луи Коши, Вильгельм Кёниг и других. Они внесли новые идеи и методы, которые дополнили и расширили теорию графов, делая ее еще более полезной и применимой.

В 20 веке теория графов продолжила свое развитие и стала активно применяться в различных областях науки и техники. Она нашла применение в компьютерных науках, транспортном планировании, социологии, биологии и других дисциплинах. С появлением компьютеров теория графов получила новый импульс развития, так как стала возможна обработка и анализ графов с большим количеством вершин и ребер.

Сегодня теория графов стала важным инструментом в решении различных задач. Она активно применяется в сетевом анализе, оптимизации маршрутов, моделировании социальных сетей и многих других областях. Развитие теории графов продолжается и позволяет ученым и инженерам получать новые знания и решать сложные задачи, которые ранее были недоступны.

Вопрос-ответ:

Кто является основателем теории графов?

Основателем теории графов считается Леонард Эйлер, швейцарский математик, который в 1736 году в своей статье «Задача о Кёнигсбергских мостах» впервые сформулировал основные понятия и определения теории графов.

Какую роль теория графов играет в математике?

Теория графов является важной областью математики, которая изучает свойства и взаимосвязи графов. Она находит применение во многих областях, таких как компьютерная наука, теория сетей, операционные исследования, криптография, социальные науки и другие.

Какие основные понятия и определения включает теория графов?

Основные понятия теории графов включают понятие вершин (точек) и ребер (линий), а также различные свойства, такие как направленность ребер, веса ребер, связность вершин и др. Теория графов также изучает различные алгоритмы и методы решения задач на графах.

Какова история развития теории графов?

Теория графов начала развиваться в XVIII веке с работ Леонарда Эйлера. Затем она получила новый импульс в XX веке благодаря работам таких математиков, как Уильям Роуэн Хамильтон, Джордж Поля, Петер Лукасевич Эрдёш и других. С тех пор теория графов продолжает развиваться и находит все новые приложения.

Какую практическую пользу можно извлечь из теории графов?

Теория графов имеет множество практических применений. Например, она может быть использована для оптимизации сетей передвижения, планирования маршрутов, анализа социальных сетей, моделирования программных систем и т.д. Благодаря теории графов можно решать сложные задачи эффективно и точно.

Применение теории графов в реальном мире

Теория графов, основанная на исследовании связей между объектами, широко применяется в различных областях реального мира. Ее методы и концепции находят свое применение в информатике, транспортной логистике, социологии, биологии и многих других дисциплинах.

В информатике теория графов используется для решения задач, связанных с поиском оптимальных путей в сетях, анализом сложности алгоритмов и моделированием связей между объектами. Например, графы могут быть использованы для построения схем баз данных, анализа социальных сетей, проектирования компьютерных сетей и многое другое.

В транспортной логистике теория графов помогает оптимизировать маршруты и расписание транспортных средств. Графы могут представлять дорожные сети, логистические цепочки, транспортные потоки и т.д. Анализ графов позволяет оптимизировать транспортные процессы, увеличить эффективность и снизить затраты.

В социологии теория графов помогает анализировать социальные сети, взаимосвязи между людьми и организациями. Графы могут представлять дружеские связи, рабочие группы, потоки информации и другие аспекты социальной жизни. Анализ графов позволяет исследовать структуру социальных сетей, выявлять ключевых актеров и изучать динамику взаимодействий.

В биологии теория графов используется для моделирования биологических сетей, таких как генетические сети, белковые взаимодействия, пищевые цепи и т.д. Графы позволяют анализировать структуру и функцию биологических систем, выявлять взаимодействия и предсказывать результаты экспериментов.

Теория графов имеет огромное значение в математике и находит применение во многих областях реального мира. Ее методы и концепции помогают анализировать, моделировать и оптимизировать сложные системы, позволяют выявлять закономерности и прогнозировать результаты. В итоге, углубляясь в изучение теории графов, мы расширяем свои знания о мире и приобретаем мощный инструмент для анализа реальных проблем и задач.

Значимость теории графов в современной науке

Одной из наиболее известных областей, где теория графов нашла свое применение, является компьютерная наука. Графы используются для моделирования сетей, алгоритмов поиска и оптимизации, а также для анализа сложности вычислений. Благодаря этому, теория графов стала неотъемлемой частью разработки программного обеспечения и построения эффективных алгоритмов.

Теория графов также активно применяется в социологии и психологии. Графы позволяют ученым анализировать социальные сети, взаимодействие людей и распространение информации. Это помогает понять социальные явления, выявить закономерности и разработать стратегии влияния на людей.

В физике и химии теория графов используется для моделирования молекулярных структур и химических связей. Графы позволяют ученым анализировать физические и химические процессы, предсказывать свойства веществ и проектировать новые материалы.

Значимость теории графов в современной науке трудно переоценить. Она содействует развитию различных областей знания и находит применение во множестве практических задач. Благодаря этому, теория графов продолжает привлекать внимание ученых и исследователей со всего мира, способствуя развитию современной науки и технологий.

Влияние основателя теории графов на другие области математики

Основатель теории графов Леонард Эйлер внес огромный вклад в различные области математики своими исследованиями и открытиями. Его работы имели огромное влияние на современную науку и оказались полезными для решения множества задач в разных областях знания.

Одной из областей математики, в которой теория графов нашла широкое применение, является теория сетей. Графы используются для моделирования различных сложных сетей, таких как электрические схемы, транспортные системы, социальные сети и т.д. Эйлеровы графы позволили решить множество задач, связанных с поиском оптимальных путей, определением наиболее надежных соединений и оценкой эффективности сетей.

Также теория графов нашла применение в области компьютерных наук. Алгоритмы, основанные на графах, используются в компьютерных сетях, базах данных, алгоритмах поиска и сортировки. Множество задач, связанных с обработкой графовой информации, могут быть решены с помощью графовых алгоритмов, разработанных благодаря исследованиям Эйлера.

Основатель теории графов также оказал влияние на теорию вероятности и математическую статистику. Графы используются для моделирования случайных процессов и решения задач, связанных с вероятностными распределениями. Эйлер внес вклад в разработку методов анализа графовых моделей, которые послужили основой для развития вероятностных методов и статистических моделей.

Теория графов также нашла применение в дискретной математике и теории алгоритмов. Множество задач, связанных с оптимизацией, планированием и комбинаторикой, могут быть сформулированы и решены с помощью графовых методов и алгоритмов. Эйлеровы графы стали основой для развития дискретной математики и теории алгоритмов, которые нашли применение в компьютерных науках и других областях.

Таким образом, вклад Леонарда Эйлера в развитие теории графов оказал существенное влияние на множество областей математики. Его работы и исследования стали основой для развития новых методов и алгоритмов, которые нашли применение в современных науках и технологиях.

Основные понятия и определения в теории графов

Основные понятия в теории графов:

ТерминОпределение

Вершина (узел)	Один из элементов графа, обозначаемый точкой или числом. Вершины могут быть соединены ребрами.
Ребро	Связь между двумя вершинами графа. Ребра могут быть направленными или ненаправленными.
Направленный граф	Граф, в котором каждое ребро имеет направление от одной вершины к другой.
Ненаправленный граф	Граф, в котором ребра не имеют направления и соединяют вершины без учета порядка.
Путь	Список вершин, соединенных ребрами. Путь может быть простым (вершины не повторяются) или циклическим (путь начинается и заканчивается в одной и той же вершине).
Связный граф	Граф, в котором между любой парой вершин существует путь.
Ориентированный граф	Граф, в котором каждое ребро имеет направление от одной вершины к другой.
Сильно связный граф	Ориентированный граф, в котором между любой парой вершин существует ориентированный путь.

Определения и понятия в теории графов играют важную роль в математике и находят применение в различных областях, таких как компьютерная наука, транспортная логистика, социальные сети и многое другое.

Перспективы развития теории графов

Одной из перспектив развития теории графов является ее применение в анализе социальных сетей. Социальные сети представляют собой графы, в которых вершины соответствуют людям, а ребра — связям между этими людьми. Анализ таких графов позволяет изучать структуру социальных связей и прогнозировать различные явления, такие как распространение информации или влияние лидеров на поведение других участников сети.

Еще одной перспективой развития теории графов является ее применение в области биологии и медицины. Графы могут быть использованы для моделирования биологических сетей, таких как сети генных регуляторов или белковых взаимодействий. Анализ таких графов позволяет лучше понять принципы работы живых систем и разрабатывать новые методы лечения и диагностики заболеваний.

Также теория графов может найти применение в области транспорта и логистики. Графы могут быть использованы для моделирования сетей дорог, железных дорог или транспортных маршрутов в городах. Анализ таких графов позволяет оптимизировать планирование маршрутов, распределение ресурсов и улучшить эффективность транспортной системы.

В целом, перспективы развития теории графов огромны. Она продолжает находить применение в различных областях и вносить вклад в развитие науки и технологий. Современные методы анализа и визуализации графов позволяют решать сложные задачи и находить новые пути для применения теории графов в различных областях жизни.