Что такое мнимое число в математике

Мнимое число в математике — это число, представляющее собой квадратный корень из отрицательного числа. Оно обозначается символом i и является важной составляющей комплексных чисел. Мнимые числа используются для решения различных задач и применяются в физике, инженерии и других научных областях. Узнайте больше о мнимых числах и их роли в математике.

Математика — это наука, которая изучает числа и их свойства. В рамках математики существуют различные типы чисел, одним из которых является мнимое число. Мнимые числа возникли в результате необходимости решения уравнений, которые не имели решений в действительных числах.

Мнимое число — это число, которое является квадратом отрицательного числа. Обычно мнимое число обозначается символом i, которое определяется как квадратный корень из -1. Таким образом, i = √(-1).

Мнимые числа можно использовать для решения уравнений, которые не имеют решений в действительных числах. Они также находят применение в различных областях науки и техники, например, в электротехнике и физике.

Примером мнимого числа может служить число 3i. В этом случае, когда число умножается на i, оно умножается на квадратный корень из -1 и становится мнимым. Таким образом, 3i является мнимым числом.

Мнимое число в математике: определение и примеры

Мнимое число i или j определяется следующим образом: i^2 = -1. Это означает, что квадрат мнимого числа равен -1. Значение мнимого числа можно увеличить или уменьшить с помощью коэффициента перед ним. Например, 2i умножается на 2 и становится 4i.

Мнимые числа играют важную роль в решении различных математических задач, особенно в области электрических цепей, теории сигналов и компьютерной графики. Они также широко используются в комплексном анализе, где мнимые числа позволяют решать уравнения, которые невозможно решить с помощью обычных действительных чисел.

Примеры мнимых чисел включают i, 2i, 3i и т.д. Мнимые числа могут быть комбинированы с действительными числами для создания комплексных чисел. Например, комплексное число 3 + 2i состоит из действительной составляющей 3 и мнимой составляющей 2i.

Определение мнимого числа

Мнимые числа обозначаются в форме a + bi, где a и b — это вещественные числа, а i — мнимая единица. Вещественная часть a называется действительной частью мнимого числа, а мнимая часть bi — мнимой частью.

Мнимые числа важны в математике и широко используются в различных областях, таких как теория сигналов, электротехника и физика. Они позволяют представлять и работать с комплексными величинами, включая фазы, импедансы и трансформации.

Примеры мнимых чисел:

• i — базовая мнимая единица
• 2i — мнимое число с мнимой частью 2
• -3i — мнимое число с мнимой частью -3
• 4 + 5i — комплексное число с действительной частью 4 и мнимой частью 5

Мнимые числа: основные характеристики

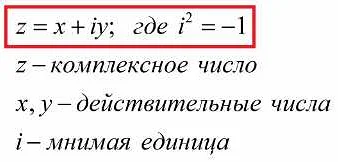
Основные характеристики мнимых чисел:

• Мнимое число обозначается символом i.
• Мнимые числа не имеют физического смысла и не могут быть измерены.
• Операции с мнимыми числами выполняются с использованием мнимой единицы i.
• Комплексное число может быть записано в виде суммы действительной и мнимой частей, например: z = a + bi, где a — действительная часть, b — мнимая часть.
• Мнимые числа используются в различных областях математики, физики и инженерии для решения различных задач.

Мнимые числа играют важную роль в комплексном анализе, алгебре и других разделах математики. Они позволяют решать уравнения, которые не имеют решений среди вещественных чисел, и представляют собой мощный инструмент для изучения различных математических моделей и физических явлений. Понимание основных характеристик мнимых чисел позволяет более глубоко понять и использовать их в различных областях науки и техники.

Мнимые числа в комплексной плоскости

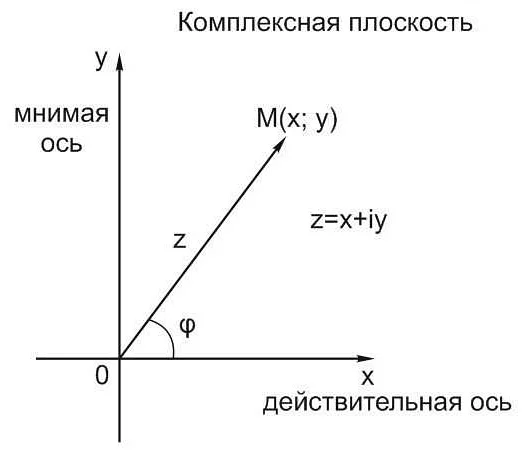
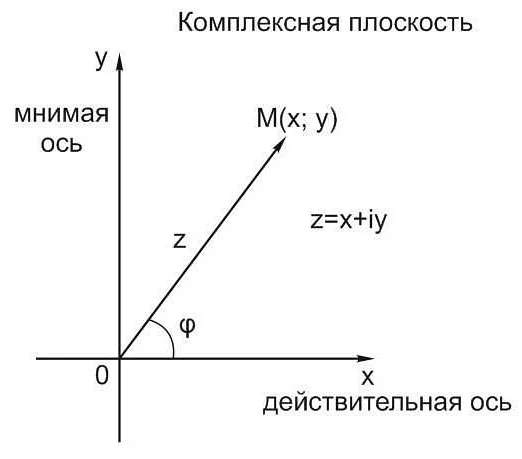
Чтобы наглядно представить мнимые числа, их можно изобразить на комплексной плоскости. Комплексная плоскость представляет собой плоскость, на которой реальные числа располагаются по горизонтальной оси, а мнимые числа – по вертикальной оси. Таким образом, каждое мнимое число соответствует точке на плоскости.

Например, если рассмотреть мнимое число 3i, то оно будет представлено на комплексной плоскости точкой, находящейся на 3 единицы выше нуля вертикальной оси. Аналогично, мнимое число -2i будет представлено точкой, находящейся на 2 единицы ниже нуля вертикальной оси.

Таким образом, комплексная плоскость позволяет наглядно представлять мнимые числа и выполнять с ними различные операции, такие как сложение, вычитание, умножение и деление. Комплексная плоскость является важным инструментом в изучении мнимых чисел и их свойств.

Примеры мнимых чисел

Мнимые числа представляют собой числа, которые невозможно представить в виде действительных чисел. Они обозначаются буквой «i», где i^2 = -1. Вот несколько примеров мнимых чисел:

1. Мнимое число i

Самым известным и простым примером мнимого числа является число i. Оно представляет собой квадратный корень из -1 и используется в комплексных числах для обозначения мнимой части.

2. Комплексные числа

Комплексные числа представляют собой комбинацию действительной и мнимой частей. Например, число 3 + 4i является комплексным числом, где 3 — действительная часть, а 4i — мнимая часть.

3. Мнимая единица

Мнимая единица обозначается как j и используется в электротехнике и схемотехнике для обозначения мнимых чисел. Она имеет такие же свойства, как и число i, и является примером мнимого числа.

4. Мнимые числа в физике

Мнимые числа также широко используются в физике для описания различных явлений. Например, в электричестве и магнетизме мнимые числа используются для математического описания переменных и фазовых сдвигов.

Это лишь некоторые примеры мнимых чисел, которые широко используются в математике, физике и других науках. Они играют важную роль в решении различных задач и являются неотъемлемой частью комплексного анализа и других отраслей математики.

Использование мнимых чисел в физике

Мнимые числа играют важную роль в физике, особенно в тех областях, где встречаются колебания и волны. Они позволяют удобно описывать фазовые сдвиги и амплитудные изменения в различных физических системах.

Одно из самых распространенных применений мнимых чисел в физике — это описание электромагнитных волн. Мнимые числа используются для описания комплексной амплитуды электрического и магнитного поля волны. Это позволяет учитывать фазовый сдвиг между полями и описывать их взаимосвязь.

Мнимые числа также применяются для описания колебаний в электрических цепях. Они позволяют учесть фазовый сдвиг между напряжением и током в цепи и описать их зависимость друг от друга. Это особенно важно при решении задач, связанных с переменным током и переменным напряжением.

Кроме того, мнимые числа играют важную роль в квантовой механике. Они используются для описания состояний частиц и их волновых функций. Мнимые числа позволяют описывать вероятности нахождения частицы в определенных местах и в определенные моменты времени.

Использование мнимых чисел в физике позволяет более точно описывать и анализировать различные физические явления и процессы. Они помогают ученым строить математические модели и решать сложные задачи, связанные с колебаниями, волнами и квантовой механикой.

Соотношение между мнимыми и действительными числами

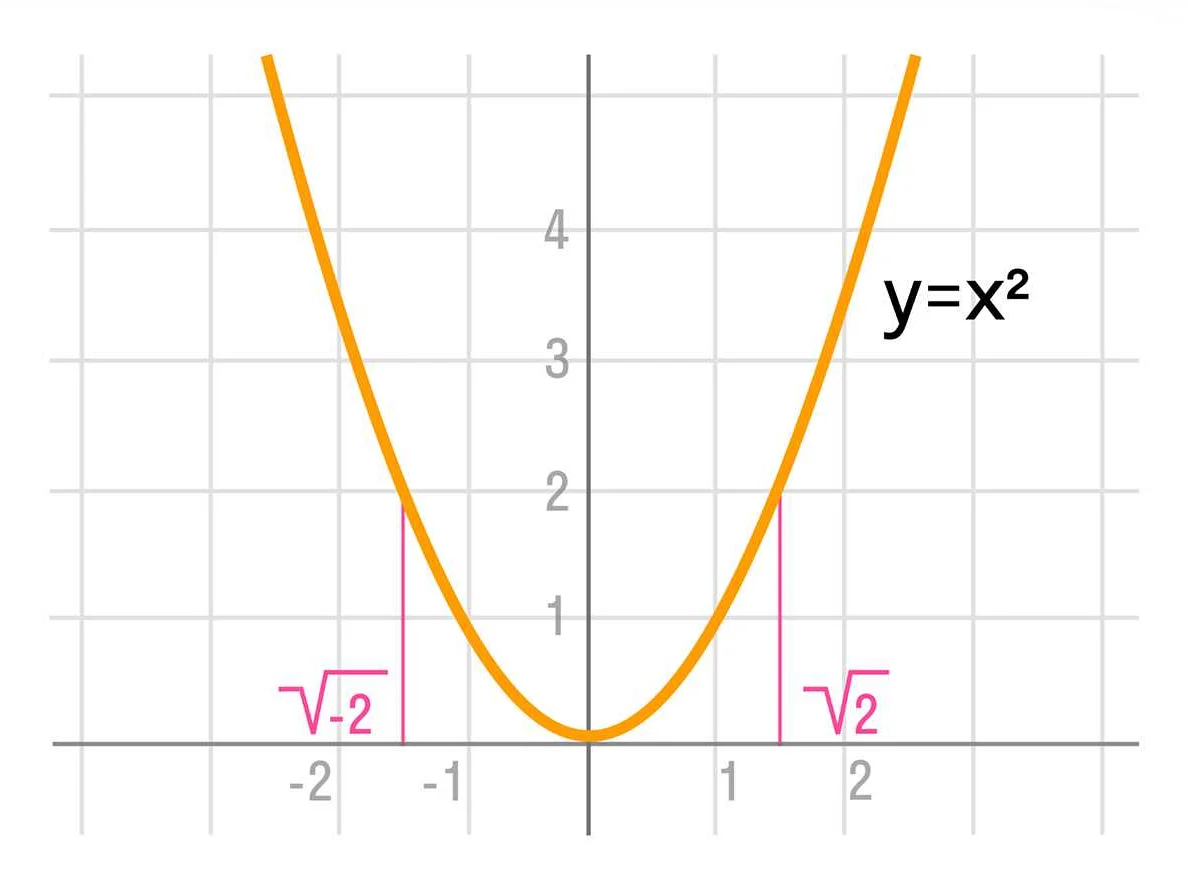
Мнимая единица i определяется как квадратный корень из -1. Она вводится для того, чтобы решать уравнения, которые не имеют решений в действительных числах. С помощью мнимых чисел можно решать уравнения вида x^2 + 1 = 0, где решением будет x = ±i.

Комплексные числа состоят из суммы действительной и мнимой части. Действительная часть представляет собой обычное число на числовой оси, а мнимая часть представляет собой число, умноженное на мнимую единицу i. Таким образом, комплексное число можно записать в виде a + bi, где a — действительная часть, а b — мнимая часть.

Отношения между мнимыми и действительными числами особенно ярко проявляются в операциях с комплексными числами. Сложение, вычитание, умножение и деление комплексных чисел осуществляется поэлементно, как сумма, разность, произведение и частное соответственно их действительных и мнимых частей.

Использование мнимых чисел в математике позволяет решать более широкий класс уравнений и применять их в различных областях науки и техники, таких как электротехника, теория сигналов и квантовая физика.

Расчеты с мнимыми числами

Мнимые числа широко применяются в математике и физике для решения различных задач. Они используются для представления величин, которые невозможно измерить в реальном мире, а также для решения уравнений, которые не имеют реальных корней.

Основные операции с мнимыми числами — сложение, вычитание, умножение и деление. Для выполнения этих операций необходимо использовать мнимую единицу, обозначаемую символом i.

При сложении или вычитании мнимых чисел схема действий аналогична сложению или вычитанию обычных чисел. Например, чтобы сложить два мнимых числа, необходимо сложить их действительные и мнимые части отдельно.

Умножение мнимых чисел можно выполнить, используя правило, согласно которому i^2 = -1. Таким образом, чтобы умножить два мнимых числа, необходимо перемножить их действительные части, вычислить произведение мнимых единиц и учесть правило i^2 = -1.

Деление мнимых чисел выполняется аналогично делению обычных чисел. Для этого необходимо разделить их действительные и мнимые части отдельно.

Пример расчета с мнимыми числами:

• Сложение: (3 + 4i) + (2 + 5i) = (3 + 2) + (4 + 5)i = 5 + 9i
• Вычитание: (3 + 4i) — (2 + 5i) = (3 — 2) + (4 — 5)i = 1 — i
• Умножение: (3 + 4i) * (2 + 5i) = (3 * 2) + (3 * 5)i + (4 * 2)i + (4 * 5 * i^2) = 6 + 15i + 8i — 20 = -14 + 23i
• Деление: (3 + 4i) / (2 + 5i) = ((3 * 2) + (4 * 5)) / ((2 * 2) + (5 * 5)) + ((4 * 2) — (3 * 5)) / ((2 * 2) + (5 * 5))i = (6 + 20) / (4 + 25) + (8 — 15) / (4 + 25)i = 26 / 29 — 7 / 29i

Таким образом, мнимые числа позволяют выполнять различные расчеты и решать задачи, которые не могут быть решены с использованием только действительных чисел.

Применение мнимых чисел в электротехнике

Мнимые числа, также известные как комплексные числа, играют важную роль в электротехнике. Они позволяют упростить и решить множество задач, связанных с электрическими цепями и сигналами.

Одной из основных областей применения мнимых чисел в электротехнике является анализ переменного тока. Мнимые числа позволяют удобно представлять величины, меняющиеся по синусоидальному закону. Здесь мнимая единица i представляет собой квадратный корень из -1.

С помощью мнимых чисел можно выразить комплексное сопротивление, которое определяет взаимодействие активного и реактивного сопротивлений в электрической цепи. Комплексное сопротивление позволяет учитывать фазовые сдвиги и реактивные потери в цепи.

Мнимые числа также используются при анализе и проектировании фильтров. Фильтры широко применяются в электронике для обработки сигналов, и мнимые числа позволяют удобно представлять их характеристики и свойства.

Кроме того, мнимые числа находят применение в теории управления и системах автоматического регулирования. Они позволяют анализировать и описывать динамические процессы в системах с обратной связью.

Примеры применения мнимых чисел в электротехнике:

Вычисление комплексного сопротивления в электрической цепи

Анализ и проектирование фильтров

Описание динамических процессов в системах управления

В заключение, мнимые числа играют важную роль в электротехнике, облегчая анализ и решение задач, связанных с электрическими цепями и сигналами. Они позволяют удобно представлять и оперировать комплексными величинами, что делает их незаменимыми в электротехнике и связанных с ней областях.

Вопрос-ответ:

Что такое мнимое число?

Мнимое число — это число, которое можно представить в виде суммы действительной и мнимой части, где мнимая часть обозначается буквой i. Например, число 2 + 3i является мнимым числом.

Как определить, что число является мнимым?

Число является мнимым, если оно содержит мнимую единицу i в своем представлении. Если число можно представить в виде a + bi, где a и b — действительные числа, то оно является мнимым.

Можно ли выполнить арифметические операции с мнимыми числами?

Да, с мнимыми числами можно выполнять арифметические операции, такие как сложение, вычитание, умножение и деление. Например, сложение двух мнимых чисел a + bi и c + di выполняется путем сложения их действительных и мнимых частей по отдельности: (a + c) + (b + d)i.

Для чего используются мнимые числа в математике?

Мнимые числа используются в математике для решения различных проблем и задач, которые не могут быть решены с использованием только действительных чисел. Они широко применяются в физике, электротехнике и других науках для описания комплексных величин, таких как электрические сопротивления, импедансы и т. д.

Какие примеры мнимых чисел можно привести?

Примерами мнимых чисел могут служить числа вида bi, где b — действительное число. Например, 2i, -5i, 0.5i — все они являются мнимыми числами. Также можно привести пример комплексного числа 3 + 4i, которое является суммой действительной и мнимой частей.

Видео по теме: