Корень что это такое в математике

Корень в математике — это операция обратная возведению в степень. Корень из числа позволяет найти число, которое нужно возвести в данную степень, чтобы получить исходное число. Узнайте, как работает корень и как его можно использовать для решения математических задач.

Корень – важное понятие в математике, которое является обратной операцией возведения в степень. Корень позволяет найти такое число, которое при возведении в определенную степень будет равно данному числу. Например, корень квадратный из числа 25 равен 5, так как 5 в квадрате равно 25.

Корень имеет свои свойства, которые делают его удобным инструментом для решения различных математических задач. Например, корень из произведения двух чисел равен произведению корней этих чисел. Также корень из частного двух чисел равен частному корней этих чисел. Корень можно выносить за знак суммы и разности, а также за знаки степени и логарифма.

Примеры использования корня в математике встречаются повсеместно. Одним из таких примеров является решение квадратного уравнения. Для нахождения корней квадратного уравнения используется формула, содержащая корень. Еще одним примером является нахождение среднего арифметического, для чего необходимо найти корень из суммы всех чисел, разделенной на их количество.

В заключение, корень – это мощный инструмент в математике, который позволяет находить решения различных задач. Знание свойств и применение корня позволяет упростить вычисления и получить точные результаты.

Определение корня в математике

Корни обозначаются символом √, который читается как «корень». Например, квадратный корень из числа 9 обозначается так: √9 = 3, так как 3 * 3 = 9. Отрицательные числа не имеют квадратного корня в вещественных числах, поэтому √-9 не имеет значения.

Корень может быть любой степени, не только квадратным. Например, кубический корень из числа 8 обозначается так: ∛8 = 2, так как 2 * 2 * 2 = 8. Также можно вычислить корень четвертой степени, пятой степени и т.д.

Корень может быть вещественным или мнимым числом. Вещественные корни находятся из неотрицательных чисел, а мнимые корни из отрицательных чисел.

Определение корня в математике является важным понятием, которое широко применяется в различных областях, таких как физика, инженерия, экономика и т.д.

Видео по теме:

Свойства корня

2. Корень из произведения: Корень из произведения двух чисел равен корню из первого числа, умноженного на корень из второго числа. То есть, если a и b — положительные числа, то √(a * b) = √a * √b.

3. Корень из частного: Корень из частного двух чисел равен корню из первого числа, деленного на корень из второго числа. То есть, если a и b — положительные числа, то √(a / b) = √a / √b.

4. Корень от корня: Корень от корня равен корню из произведения этих двух корней. То есть, если a и b — положительные числа, то √(√a) = √(a)^(1/2) = a^(1/4).

5. Корень из числа, возведенного в степень: Корень из числа, возведенного в степень, равен числу, возведенному в эту степень, поделенному на саму степень. То есть, если a — положительное число и n — натуральное число, то √(a^n) = a^(n/2).

6. Корень из отрицательного числа: Корень из отрицательного числа не имеет действительных значений в рамках действительных чисел. Вместо этого, для вычисления корня из отрицательного числа, вводится понятие комплексных чисел.

Использование этих свойств позволяет упростить вычисления и решение уравнений, содержащих корень.

Примеры корней в математике

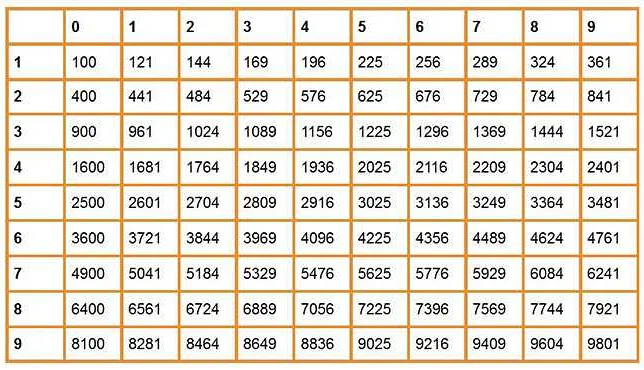
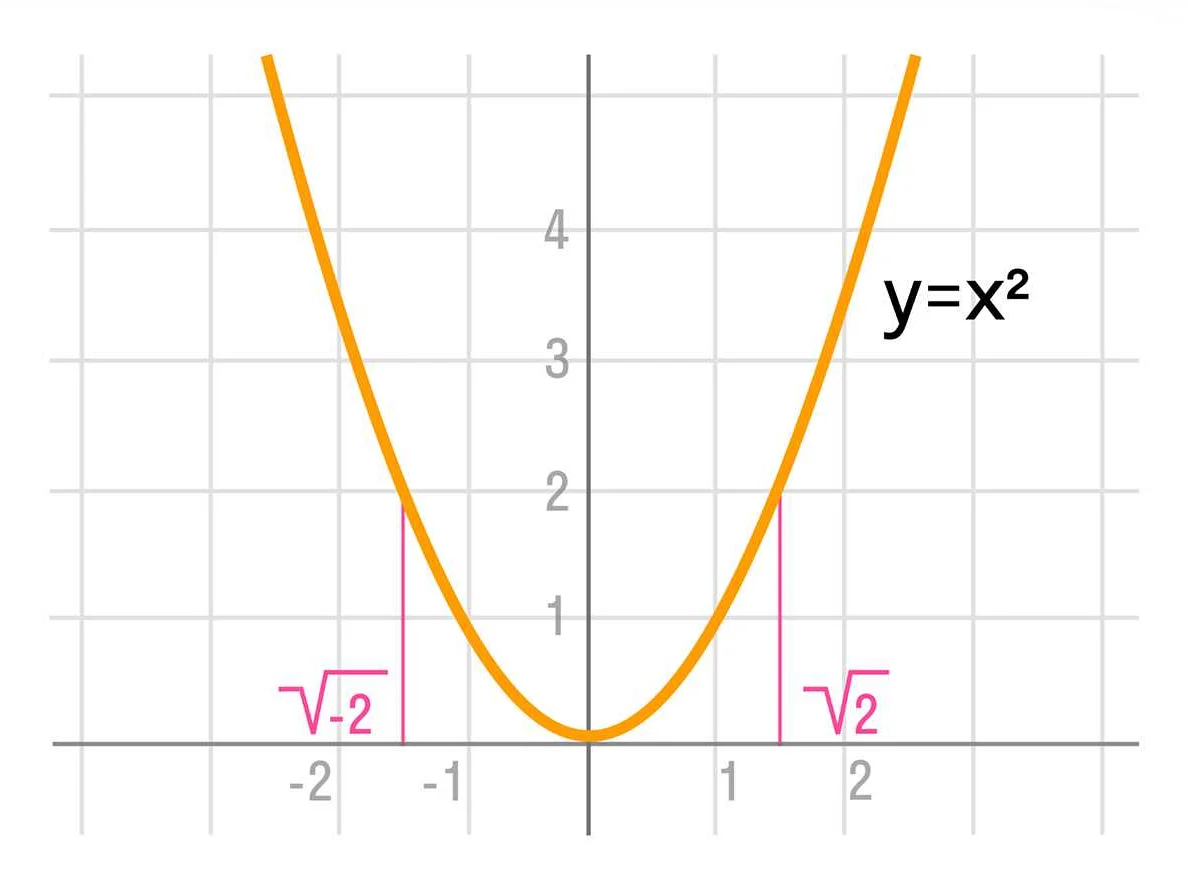
Существует несколько разных типов корней в математике. Вот несколько примеров:

1. Квадратный корень: квадратный корень из числа а обозначается как √а. Например, √4 = 2, так как 2 × 2 = 4.

2. Кубический корень: кубический корень из числа а обозначается как ∛а. Например, ∛8 = 2, так как 2 × 2 × 2 = 8.

3. Корень n-ой степени: корень n-ой степени из числа а обозначается как √nа. Например, ∛27 = 3, так как 3 × 3 × 3 = 27.

4. Комплексные корни: в комплексных числах существуют корни отрицательных чисел и чисел, не являющихся точными степенями.

Это лишь некоторые примеры корней в математике. Корни широко используются в различных областях науки, техники и финансов.

Рациональные и иррациональные корни

Иррациональные корни – это корни, которые не могут быть представлены в виде дроби и не могут быть точно выражены в виде конечного числа. Например, корни вида √2, √3 и √5 являются иррациональными корнями, так как их десятичные представления являются бесконечными и непериодическими десятичными дробями.

Рациональные и иррациональные корни имеют ряд свойств:

1. Сумма или разность двух рациональных корней всегда будет рациональным корнем.
2. Произведение двух рациональных корней всегда будет рациональным корнем.
3. Сумма или разность рационального корня и иррационального корня всегда будет иррациональным корнем.
4. Произведение рационального корня и иррационального корня всегда будет иррациональным корнем.

Например, √2 + 2/3 является иррациональным корнем, так как эта сумма содержит иррациональный корень √2. А √3 * 4/5 является иррациональным корнем, так как эта произведение содержит иррациональный корень √3.

Корень как операция

Корень может быть как целым числом, так и десятичной дробью. Если число не является точным квадратом, то корень из него будет десятичной дробью, которую можно приблизительно выразить с определенной точностью.

Свойства корня:

СвойствоПример

Корень из суммы	√(a + b)
Корень из произведения	√(a * b)
Корень из разности	√(a — b)
Корень из частного	√(a / b)
Корень из корня	√(√a)

Примеры использования корня:

• Корень из 25 равен 5, так как 5^2 = 25.
• Корень из 9 равен 3, так как 3^2 = 9.
• Корень из 2 равен примерно 1,414, так как 1,414^2 ≈ 2.

Корень как операция широко используется в различных областях математики, физики, инженерии и других науках. Он позволяет находить решения уравнений, вычислять площади фигур, определять значения функций и многое другое.

Формулы с корнем

Одна из самых известных формул с корнем – формула дискриминанта. Она используется для нахождения корней квадратного уравнения. Дискриминант равен разности между квадратом коэффициента при x в уравнении и удвоенным произведением коэффициента при x в уравнении и свободного члена. Если дискриминант положителен, то уравнение имеет два различных корня, если дискриминант равен нулю, то уравнение имеет один корень, а если дискриминант отрицателен, то уравнение не имеет действительных корней.

Еще одна формула с корнем – формула Герона. Она используется для нахождения площади треугольника по длинам его сторон. Формула выглядит следующим образом: S = √(p(p-a)(p-b)(p-c)), где S – площадь треугольника, а, b, c – длины его сторон, а p – полупериметр треугольника.

Также существуют формулы с корнем в различных областях математики, такие как формула Ньютона-Лейбница, формула Эйлера и многие другие. Корни являются важным понятием и имеют широкое применение в различных математических задачах и формулах.

Положительный и отрицательный корень

Положительный корень обозначается символом √x, где x — число, из которого извлекается корень. Если x является положительным числом, то положительный корень равен положительному числу и обозначает значение переменной.

Например, корень из 9 равен 3, так как 3 * 3 = 9. В данном случае положительный корень равен положительному числу 3.

Отрицательный корень обозначается символом -√x и используется для нахождения отрицательного значения переменной. Он применяется в случаях, когда переменная имеет отрицательное значение или уравнение подразумевает отрицательный результат.

Например, корень из -9 равен -3, так как -3 * -3 = 9. В данном случае отрицательный корень равен отрицательному числу -3.

Важно учитывать, что корень из отрицательного числа вещественный и обозначается символом i, который представляет мнимую единицу.

Таким образом, положительный и отрицательный корень представляют разные значения переменной в зависимости от указанного знака. Их использование позволяет решать уравнения и находить значения переменных в различных ситуациях.

Решение уравнений с корнем

Для решения уравнений с корнем следует выполнить следующие шаги:

1. Перенести корень на одну сторону уравнения.
2. Возвести обе части уравнения в квадрат, чтобы избавиться от корня.
3. Решить полученное квадратное уравнение.
4. Проверить полученные решения, подставив их в исходное уравнение.

Пример решения уравнения с корнем:

Дано уравнение √(x+3) = 5. Применим описанные выше шаги для его решения:

Шаг 1: Переносим корень на одну сторону уравнения: √(x+3) — 5 = 0.

Шаг 2: Возводим обе части уравнения в квадрат: (x+3) — 5^2 = 0.

Шаг 3: Решаем полученное квадратное уравнение: x+3 — 25 = 0, x — 22 = 0, x = 22.

Шаг 4: Проверяем полученное решение, подставив его в исходное уравнение: √(22+3) = 5, √25 = 5, 5 = 5.

Таким образом, решением уравнения √(x+3) = 5 является x = 22.

Вопрос-ответ:

Что такое корень в математике?

Корень в математике — это число, которое при возведении в заданную степень дает другое число. Например, корень квадратный (или просто квадратный корень) из числа 9 равен 3, так как 3 в квадрате равно 9. Корень может быть извлечен из любого неотрицательного числа, и результатом всегда будет положительное число или ноль.

Как вычислить корень из числа?

Вычисление корня из числа можно выполнить с помощью калькулятора или математической программы. В случае квадратного корня, можно использовать формулу извлечения корня или воспользоваться функцией квадратного корня в программе. Для более сложных корней, таких как кубический корень или корень n-ой степени, требуется использовать специальные методы и алгоритмы.

Какие свойства имеет корень в математике?

Корень обладает несколькими свойствами, которые могут быть использованы при решении математических задач. Некоторые из них включают: свойство корня из произведения (корень из произведения двух чисел равен произведению корней этих чисел), свойство корня из частного (корень из частного двух чисел равен частному корней этих чисел), свойство корня из степени (корень из числа, возведенного в степень, равен числу, возведенному в эту степень), и другие.

Какие примеры можно привести для корня в математике?

Вот несколько примеров использования корня в математике: вычисление квадратного корня из числа, например, корень из 25 равен 5; вычисление кубического корня, например, корень кубический из 8 равен 2; вычисление корня n-ой степени, например, корень четвертой степени из 16 равен 2. Также, корни часто используются для решения квадратных уравнений и других математических задач.