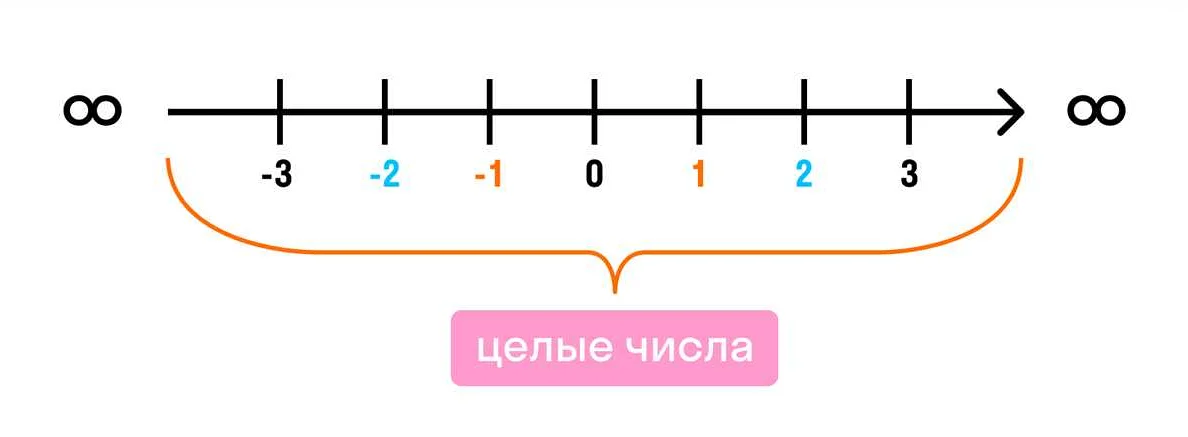
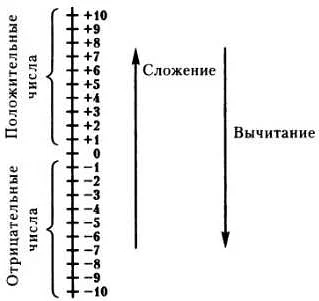
Что называют натуральным числом в математике

Натуральное число в математике — это положительное целое число, которое используется для подсчета и измерения. Оно включает в себя числа от 1 и выше, и является основной составляющей в арифметических операциях и математических моделях. Узнайте больше о понятии натурального числа и его роли в математике на нашем сайте.

Натуральные числа являются одной из основных и наиболее простых групп чисел в математике. Они представляют собой положительные целые числа, начиная с единицы и продолжая бесконечно вправо. В математической записи натуральные числа обозначаются символом N.

Натуральные числа используются для подсчета и упорядочивания объектов, которые являются единичными и неотрицательными. Они позволяют нам отвечать на вопросы, сколько объектов находится в данной группе или как они могут быть упорядочены.

Натуральные числа являются фундаментальными в математике и широко применяются во многих областях науки. Они играют важную роль в арифметике, алгебре, геометрии, теории чисел и других разделах математики.

Одной из основных особенностей натуральных чисел является их способность образовывать бесконечную последовательность. Каждое натуральное число имеет свое следующее число, которое находится на единицу большее. Это свойство позволяет нам выполнять различные операции с натуральными числами, такие как сложение, вычитание, умножение и деление.

Натуральные числа: определение и свойства

Основные свойства натуральных чисел:

СвойствоОписание

Замкнутость относительно сложения и умножения	Сумма или произведение двух натуральных чисел также является натуральным числом.
Ассоциативность сложения и умножения	Результат сложения или умножения не зависит от порядка складываемых или умножаемых чисел.
Коммутативность сложения и умножения	Порядок слагаемых или множителей не влияет на результат сложения или умножения.
Существование нейтральных элементов	Существует натуральное число, которое не изменяет другое число при сложении или умножении.
Существование обратного элемента	Для каждого натурального числа существует другое натуральное число, при сложении или умножении с которым результат будет равен нейтральному элементу.

Натуральные числа играют важную роль в математике, используются в различных областях, таких как арифметика, алгебра, теория чисел и др. Они являются основой для построения системы натуральных чисел.

Видео по теме:

Что такое натуральные числа в математике

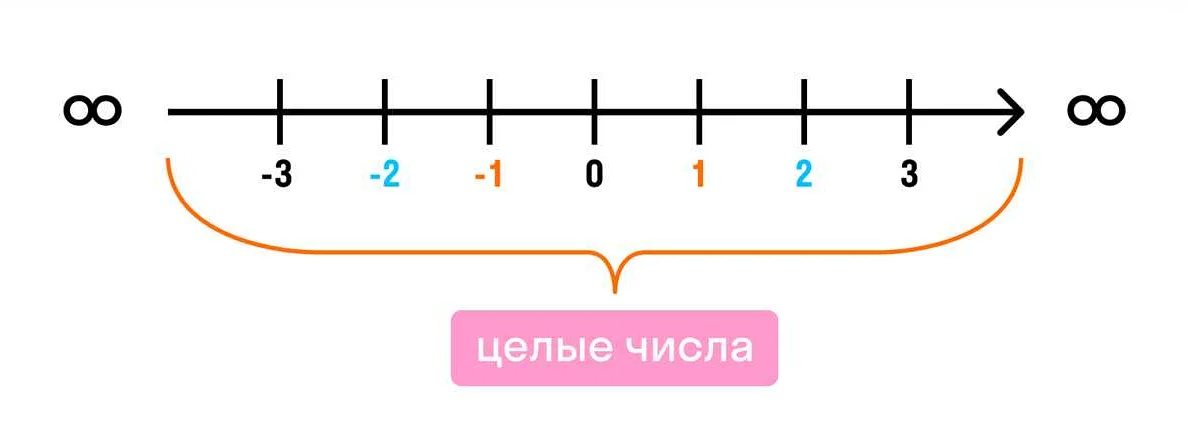
Натуральные числа используются для подсчета объектов, количества и порядка. Они являются основой для других математических операций и позволяют совершать арифметические действия, такие как сложение, вычитание, умножение и деление.

Натуральные числа обладают следующими свойствами:

1. Каждое натуральное число имеет преемника — следующее число, которое на единицу больше. Например, преемником числа 5 является число 6.
2. Каждое натуральное число, кроме единицы, имеет предшественника — предыдущее число, которое на единицу меньше. Например, предшественником числа 5 является число 4.
3. Натуральные числа можно складывать, вычитать, умножать и делить, получая другие натуральные числа.
4. Множество натуральных чисел является бесконечным и несчетным.

Натуральные числа играют важную роль в математике и широко применяются в различных областях науки и повседневной жизни.

Как определяются натуральные числа

Определение натуральных чисел можно представить в виде списка свойств:

1. Натуральные числа начинаются с единицы и продолжаются бесконечно.
2. Натуральные числа являются положительными целыми числами.
3. Натуральные числа используются для подсчета или упорядочения предметов в реальном мире.
4. Каждое натуральное число имеет следующее число — его преемника.
5. Порядок натуральных чисел определяется их величиной: чем больше число, тем позже оно в последовательности.

Некоторые математики также включают ноль в натуральные числа, но это не всеобщее соглашение.

Натуральные числа играют важную роль в математике, физике, информатике и других науках. Они используются для моделирования различных явлений и процессов и предоставляют базовую арифметическую систему для выполнения операций сложения, вычитания, умножения и деления.

Свойства натуральных чисел

1. Замкнутость относительно сложения и умножения:

Натуральные числа замкнуты относительно операций сложения и умножения, то есть сумма или произведение двух натуральных чисел также является натуральным числом.

2. Ассоциативность сложения и умножения:

Для любых трех натуральных чисел a, b и c справедливо следующее свойство: (a + b) + c = a + (b + c) и (a * b) * c = a * (b * c).

3. Коммутативность сложения и умножения:

Сумма и произведение двух натуральных чисел не зависят от порядка слагаемых или множителей, то есть a + b = b + a и a * b = b * a.

4. Существование нейтрального элемента:

Для сложения натуральных чисел существует натуральное число 0, которое является нейтральным элементом относительно этой операции, то есть a + 0 = a для любого натурального числа a.

Для умножения натуральных чисел существует натуральное число 1, которое является нейтральным элементом относительно этой операции, то есть a * 1 = a для любого натурального числа a.

5. Существование обратного элемента:

Для каждого натурального числа a существует такое натуральное число b, что a + b = 0. Однако обратного элемента относительно умножения для натуральных чисел не существует.

6. Свойства отношения порядка:

Натуральные числа обладают свойствами отношения порядка: для любых двух натуральных чисел a и b выполняется либо a < b, либо a > b, либо a = b.

Кроме того, для любых трех натуральных чисел a, b и c справедливо следующее свойство: если a < b и b < c, то a < c.

Натуральные числа и алгебраические операции

В математике существует несколько алгебраических операций, которые можно выполнять над натуральными числами. Эти операции включают в себя сложение, вычитание, умножение и деление.

Сложение — это операция, которая соединяет два или более натуральных числа, чтобы получить их сумму. Например, сумма чисел 3 и 4 равна 7.

Вычитание — это операция, которая позволяет вычесть одно натуральное число из другого. Вычитание может быть выполнено только в том случае, если результат неотрицательный. Например, разность чисел 7 и 3 равна 4.

Умножение — это операция, которая позволяет умножить одно натуральное число на другое, чтобы получить их произведение. Например, произведение чисел 2 и 5 равно 10.

Деление — это операция, которая позволяет разделить одно натуральное число на другое, чтобы получить их частное. Результат деления может быть целым числом или десятичной дробью. Например, частное чисел 8 и 2 равно 4.

Алгебраические операции над натуральными числами имеют свои особенности и правила, которые позволяют выполнять их безошибочно. Например, умножение натуральных чисел коммутативно, то есть порядок чисел не влияет на результат умножения.

Знание основных алгебраических операций позволяет выполнять простые и сложные вычисления с натуральными числами и решать различные математические задачи.

Четные и нечетные натуральные числа

Натуральные числа делятся на две основные категории: четные и нечетные. Четные числа можно разделить на две группы: четные числа, которые делятся на 2 без остатка, и нуль. Нечетные числа, напротив, не делятся на 2 без остатка.

Четные числа можно представить в виде 2n, где n — натуральное число. Например, 2, 4, 6, 8 и так далее. Нуль также является четным числом и может быть представлен как 2 * 0.

Нечетные числа можно представить в виде 2n + 1, где n — натуральное число. Например, 1, 3, 5, 7 и так далее. Обратите внимание, что нуль не является нечетным числом, так как оно не удовлетворяет условию 2n + 1.

Четные и нечетные числа обладают различными свойствами и могут быть использованы для решения различных задач. Например, четные числа легко суммируются, так как каждое четное число можно представить как сумму двух других четных чисел или сумму четного числа и нуля. Нечетные числа, напротив, имеют свои особенности в арифметических операциях.

Четные числаНечетные числа

2	1
4	3
6	5

Сравнение натуральных чисел

Для определения, какое число из двух больше, нужно сравнить их разряды начиная с самого старшего разряда. Если разряды равны, то нужно сравнить следующий более младший разряд. Продолжая сравнивать разряды до тех пор, пока не будет найден разряд, в котором числа отличаются, можно определить, какое число больше.

Например, чтобы сравнить числа 325 и 248, нужно сравнить первый разряд (3 и 2). Поскольку 3 больше 2, число 325 больше числа 248. Если разряды равны, нужно перейти к следующему разряду и продолжить сравнение.

Также сравнивать можно числа, записанные в разных системах счисления. Для этого нужно привести числа к одной системе счисления и затем сравнить их, следуя вышеописанному алгоритму.

СимволОперацияПример

	Меньше	3 < 5
>	Больше	7 > 2
=	Равно	4 = 4

Используя операции сравнения, можно решать различные задачи, связанные с сравнением натуральных чисел, такие как сортировка чисел по возрастанию или убыванию, определение наименьшего и наибольшего числа в наборе и другие.

Натуральные числа и простые числа

Простые числа — это натуральные числа, которые имеют ровно два различных делителя: единицу и само число. Простые числа не могут быть разложены на более мелкие множители. Примеры простых чисел: 2, 3, 5, 7, 11 и т.д.

Существует бесконечное количество натуральных чисел, но не все они являются простыми. Например, число 4 является натуральным числом, но оно имеет более двух делителей (1, 2, 4), поэтому оно не является простым числом.

Простые числа играют важную роль в математике и криптографии. Они используются для шифрования информации и проверки простоты других чисел. Изучение простых чисел позволяет нам лучше понять структуру числового множества и проводить различные исследования и доказательства в математике.

Важно: Простые числа являются фундаментальными элементами в теории чисел и они играют важную роль в различных областях математики и приложениях в реальной жизни.

Применение натуральных чисел в математике и реальной жизни

В математике:

Натуральные числа широко применяются в математике для описания и изучения различных явлений. Они используются в алгебре, геометрии, теории чисел и других разделах математики.

В алгебре натуральные числа используются в операциях сложения, вычитания, умножения и деления. Они также используются для решения уравнений и систем уравнений.

В геометрии натуральные числа могут быть использованы для описания количества объектов, таких как точки, линии, углы и многоугольники. Они также используются для измерения длины, площади и объема.

В теории чисел натуральные числа изучаются в контексте их свойств и взаимоотношений. Например, простые числа, числа Фибоначчи, совершенные числа и другие классы чисел являются объектами исследования.

В реальной жизни:

Натуральные числа также имеют применение во многих сферах реальной жизни. Они используются для счета, измерения количества и установления порядка.

В повседневной жизни мы используем натуральные числа для подсчета предметов, денег, времени, людей и других объектов. Например, мы можем посчитать, сколько яблок у нас есть, сколько денег мы потратили или сколько времени мы провели в определенном месте.

Натуральные числа также используются в различных профессиональных областях, таких как экономика, физика, биология и техника. В экономике они могут быть использованы для моделирования и анализа рыночных тенденций и процессов. В физике они используются для измерения физических величин, таких как масса, скорость и время. В биологии они могут быть использованы для изучения популяций, генетических свойств и эволюции. В технике они используются для проектирования, измерения и управления различными системами.

Таким образом, натуральные числа играют важную роль в математике и имеют широкое применение в реальной жизни.

Вопрос-ответ:

Что такое натуральные числа в математике?

Натуральные числа — это целые положительные числа, начиная с единицы и продолжающиеся до бесконечности. Обозначаются они символом N.

Какие свойства имеют натуральные числа?

Натуральные числа обладают рядом свойств, таких как ассоциативность, коммутативность и дистрибутивность при сложении и умножении. Они также удовлетворяют принципу индукции и могут быть упорядочены по возрастанию.

Могут ли натуральные числа быть отрицательными или дробными?

Натуральные числа определяются как целые положительные числа, поэтому они не могут быть отрицательными или дробными. Они начинаются с единицы и продолжаются до бесконечности без пропусков или повторов.

Как использовать натуральные числа в практических задачах?

Натуральные числа широко используются в различных областях практической деятельности, таких как счет, измерение, перечисление и классификация. Они используются для описания количественных характеристик различных объектов, а также в решении задач, связанных с подсчетом, упорядочиванием и сравнением количества.