Что такое округление в математике

Округление — это процесс приведения числа к ближайшему целому значению, с учетом определенных правил. В математике округление широко используется для упрощения вычислений и представления чисел в удобной форме. Округление может быть произведено в большую или меньшую сторону, в зависимости от правил округления и требований задачи. Понимание основных принципов округления поможет в точном представлении чисел и избегания ошибок при вычислениях.

Округление чисел — это процесс приведения числа к ближайшему целому или дробному значению в соответствии с определенными правилами. В математике округление широко используется для упрощения вычислений и представления чисел с ограниченной точностью.

Принцип округления основан на том, что каждое число можно представить в виде целой и дробной части. Целая часть числа остается неизменной, а дробная часть может быть изменена в зависимости от заданных правил округления.

Существуют различные правила округления, которые определяют, каким образом дробная часть числа будет округлена. Например, одно из наиболее распространенных правил — «округление до ближайшего целого». При использовании этого правила, число округляется до ближайшего целого числа. Если дробная часть числа равна или больше 0.5, то число округляется в большую сторону, если дробная часть меньше 0.5, то число округляется в меньшую сторону.

Например, число 3.7 будет округлено до 4, а число 3.2 будет округлено до 3.

Округление также может быть проведено до определенного количества знаков после запятой. Например, при округлении числа 3.14159 до трех знаков после запятой, получим число 3.142.

Важно помнить, что округление может влиять на точность вычислений и результаты математических операций. Поэтому при округлении чисел необходимо учитывать необходимую точность и правила округления, чтобы избежать ошибок и искажений результатов.

Что такое округление в математике?

Округление применяется в различных областях, где точность чисел не является критической, но требуется упростить и удобно представить результат.

Округление чисел может быть выполнено по разным правилам и принципам, в зависимости от конкретной задачи. Существуют следующие основные методы округления:

МетодОписание

Округление до ближайшего целого	Число округляется до ближайшего целого числа. Если десятичная часть числа равна 0.5, то число округляется до ближайшего четного целого.
Округление вниз	Число округляется до наибольшего целого числа, которое не превышает исходное число.
Округление вверх	Число округляется до наименьшего целого числа, которое не меньше исходного числа.
Округление к нулю	Число округляется до ближайшего целого числа в сторону нуля.
Округление к бесконечности	Число округляется до наибольшего целого числа в сторону бесконечности.

Выбор метода округления зависит от особенностей задачи и области применения. Некоторые методы округления могут быть более удобными или точными в определенных ситуациях.

Определение округления чисел

При округлении чисел обычно используются следующие правила:

• Округление в большую сторону: если первая цифра после запятой больше или равна 5, то число округляется в большую сторону. Например, число 3.6 округляется до 4.
• Округление в меньшую сторону: если первая цифра после запятой меньше 5, то число округляется в меньшую сторону. Например, число 3.4 округляется до 3.
• Округление до ближайшего четного числа: если первая цифра после запятой равна 5, то число округляется до ближайшего четного числа. Например, число 3.5 округляется до 4.

Округление чисел широко применяется в различных областях, включая физику, финансы, статистику и программирование. Правильное округление чисел позволяет получать более точные и удобные результаты при выполнении вычислений.

Принципы округления чисел

При округлении чисел в математике существуют основные принципы, которые определяют, какое значение будет выбрано в результате округления:

1. Принцип ближайшего целого числа: число округляется до ближайшего целого числа. Если десятичная часть числа находится на границе двух целых чисел, то округление производится в сторону более близкого числа.
2. Принцип отсечения: число округляется до наиболее близкого меньшего целого числа. При этом все десятичные знаки после указанного разряда отбрасываются.
3. Принцип дополнения: число округляется до наиболее близкого большего целого числа. При этом все десятичные знаки после указанного разряда отбрасываются.
4. Принцип банковского округления: число округляется до ближайшего кратного указанной точности. Если десятичная часть числа находится на полпути между двумя кратными числами, то округление производится в сторону четного числа.

Выбор принципа округления зависит от контекста и требований задачи, поэтому важно учитывать эти принципы при работе с округлением чисел.

Правила округления десятичных чисел

При округлении десятичных чисел применяются следующие правила:

1. Если десятичная часть числа меньше 0.5, то число округляется в меньшую сторону, т.е. просто отбрасывается десятичная часть.
2. Если десятичная часть числа больше или равна 0.5, то число округляется в большую сторону, т.е. к целому числу прибавляется единица.
3. Если десятичная часть числа равна 0.5, то число округляется к ближайшему четному числу.

Например:

• Число 3.2 округляется до 3, так как десятичная часть меньше 0.5.
• Число 6.8 округляется до 7, так как десятичная часть больше или равна 0.5.
• Число 4.5 округляется до 4, так как десятичная часть равна 0.5 и число округляется к ближайшему четному числу.

Правила округления дробных чисел

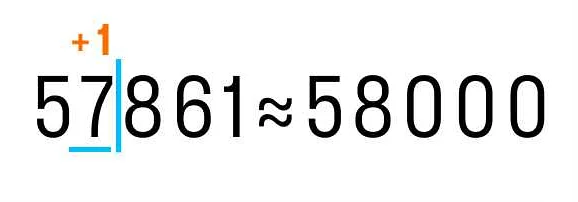
При округлении дробных чисел существуют определенные правила, которые помогают определить, какое число следует выбрать:

1. Округление до ближайшего целого числа:

Если дробная часть числа равна или меньше 0,5, то число округляется до ближайшего меньшего целого числа. Например, число 3,4 округляется до 3.

Если дробная часть числа больше 0,5, то число округляется до ближайшего большего целого числа. Например, число 3,6 округляется до 4.

2. Округление до определенного количества знаков после запятой:

Если необходимо округлить число до определенного количества знаков после запятой, то:

— Если следующий за последним оставляемым знаком равен или меньше 4, то оставляем последний оставляемый знак без изменений. Например, число 3,1416 округляется до 3,141.

— Если следующий за последним оставляемым знаком больше 4, то последний оставляемый знак увеличиваем на 1. Например, число 3,1416 округляется до 3,142.

Примечание: При округлении числа следует учитывать не только последний оставляемый знак, но и предыдущие знаки, так как они могут влиять на округление.

Округление до ближайшего целого числа

Если десятичная дробная часть числа меньше или равна 0.5, то число округляется вниз до ближайшего меньшего целого числа. Например, число 4.2 округляется до 4.

Если десятичная дробная часть числа больше 0.5, то число округляется вверх до ближайшего большего целого числа. Например, число 4.8 округляется до 5.

Исходное числоОкругленное число

4.2	4
4.8	5
5.5	6

При округлении до ближайшего целого числа некоторые числа могут округляться как вверх, так и вниз. Например, число 5.5 можно округлить как до 5, так и до 6, в зависимости от требований округления.

Округление до ближайшего целого числа широко используется во многих областях, включая финансы, статистику и программирование. Этот метод позволяет получить более удобные и понятные значения чисел, приближенные к реальным данным.

Видео по теме:

Вопрос-ответ:

Что такое округление в математике?

Округление в математике — это процесс, при котором число приближается до определенной точности. В результате округления, число заменяется другим числом, которое имеет меньшее количество значащих цифр или десятичных знаков. Округление используется для упрощения вычислений, представления чисел в удобной форме и устранения избыточной информации.

Какие принципы лежат в основе округления чисел?

Округление чисел основано на нескольких принципах. Один из них — это принцип арифметического округления, согласно которому, если десятичная часть числа больше или равна 0.5, то число округляется в большую сторону, а если десятичная часть числа меньше 0.5, то число округляется в меньшую сторону. Еще один принцип — это округление до ближайшего четного числа, которое используется, например, при округлении дробных чисел с нечетными десятичными значениями.

Какие правила существуют для округления чисел?

Существуют различные правила для округления чисел. Один из распространенных способов округления — это округление по правилу «банковского» округления, согласно которому, если десятичная часть числа равна 0.5, то число округляется в сторону четного числа. Если десятичная часть числа больше 0.5, то число округляется в большую сторону, а если десятичная часть числа меньше 0.5, то число округляется в меньшую сторону. Другое правило — это округление до заданного количества знаков после запятой, при этом, если следующая цифра больше или равна 5, то число округляется в большую сторону.

Какие последствия может иметь округление чисел?

Округление чисел может привести к некоторым последствиям. Например, при многократном округлении чисел, возможно накопление ошибок округления, что может привести к неточным результатам. Также округление может привести к потере некоторой информации, особенно если число округляется до меньшего количества знаков. В некоторых случаях округление может привести к искажению распределения данных или ошибке в вычислениях. Поэтому важно правильно выбирать метод округления, учитывая конкретную задачу и требования точности.

Округление в большую сторону

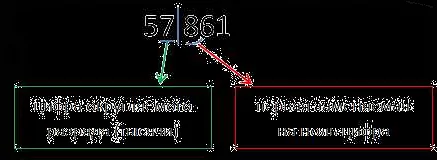
Правила округления в большую сторону следующие:

1. Если дробная часть числа больше или равна 0.5, то число округляется в большую сторону до целого числа.
2. Если дробная часть числа меньше 0.5, то число округляется до целого числа, предшествующего данному числу.

Например, если у нас есть число 3.7, то при округлении в большую сторону оно станет равным 4. А если у нас есть число 3.2, то при округлении в большую сторону оно также станет равным 4.

Округление в большую сторону может быть полезным, когда нам нужно получить наиболее близкое большее значение к исходному числу. Это может быть полезно, например, при работе с финансовыми данными, где нужно округлить сумму до целого числа в большую сторону для точного подсчета.

Важно помнить, что округление в большую сторону может влиять на точность вычислений, поэтому при необходимости следует учитывать особенности округления и его влияние на окончательные результаты.

Округление в меньшую сторону

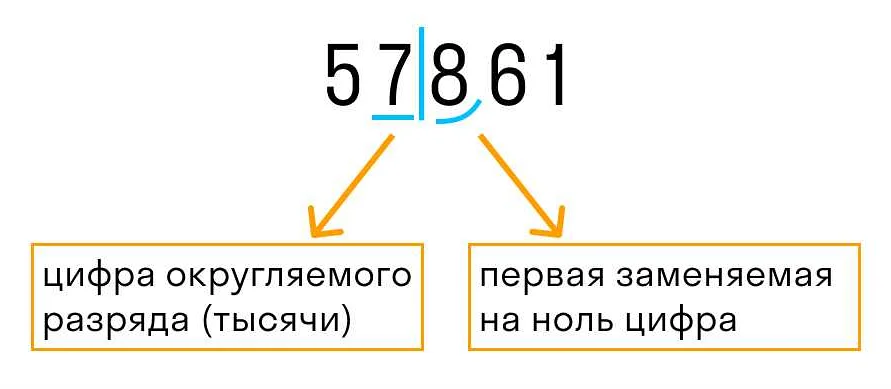
При округлении в меньшую сторону, десятичная часть числа отбрасывается, а целая часть числа остается без изменений или уменьшается на единицу.

Например, число 7.8 при округлении в меньшую сторону будет равно 7, а число 3.2 при округлении в меньшую сторону будет равно 3.

Математически округление в меньшую сторону можно представить следующим образом:

Округление в меньшую сторону: если десятичная часть числа меньше 0.5, то целая часть числа остается без изменений. Если десятичная часть числа больше или равна 0.5, то целая часть числа уменьшается на единицу.

Например, число 7.3 при округлении в меньшую сторону будет равно 7, так как десятичная часть числа меньше 0.5. А число 8.7 при округлении в меньшую сторону будет равно 8, так как десятичная часть числа больше 0.5.

Округление в меньшую сторону часто используется, когда требуется получить наиболее консервативную или наименьшую оценку, например, при расчете затрат или оценке вероятности.