Математический софизм: что это значит и как избегать ошибок при решении задач?

Математический софизм — это логическая ошибка, при которой используются неверные или несостоятельные аргументы для доказательства какого-либо утверждения в области математики. Понимание принципов математической логики поможет избежать таких ошибок и достичь правильных выводов.

Математика является одним из самых важных предметов в нашей жизни. Она не только помогает нам решить различные проблемы в повседневной жизни, но и является краеугольным камнем в научных и технологических разработках. Однако, в процессе работы с математикой мы можем столкнуться с ситуацией, когда правильность наших вычислений оказывается под вопросом. Это может быть связано с математическим софизмом.

Математический софизм — это трюк, используемый для ввода в заблуждение или уклонения от ответа. Это может быть намеренным и осуществляться с помощью обмана, или быть непреднамеренным, вызванным ошибками в логических выводах или в самом вычислении.

Чтобы избежать математического софизма, необходимо обладать хорошим пониманием основ математики и развивать критическое мышление. Важно внимательно анализировать каждый элемент задачи и по возможности использовать несколько различных методов для проверки правильности решения. Также полезно убедиться в правильности начальных данных и тщательно следить за каждым шагом вычислений.

В этой статье мы рассмотрим наиболее распространенные типы математических софизмов и предоставим практические советы по их предотвращению.

Математический софизм: ошибки в вычислениях

Математика — точная наука, но даже здесь можно допустить ошибку в вычислениях, которая может привести к серьезным последствиям. Причинами таких ошибок могут быть невнимательность, неправильное понимание формул и опечатки при записи чисел.

Один из распространенных математических софизмов — это использование неправильного порядка действий при выполнении вычислений. Если изменить порядок действий, то результат также изменится. Например, 3 + 4 × 5 будет равно 23, а не 35.

Другой возможный софизм, который может возникнуть, это отсутствие учета знака при вычитании чисел. Если забыть поставить знак минус перед числом, которое нужно вычесть, то результат будет неверным. Например, 8 — 3 будет равно 5, а не 11.

Чтобы избежать ошибок в вычислениях, необходимо быть внимательным и аккуратным при работе с числами. Никогда не нужно спешить и бросаться на подсчеты сразу, не разобравшись в формуле и задании. Также полезно проверять выполненные вычисления несколько раз и использовать калькулятор для сложных и объемных расчетов.

Видео по теме:

Что такое математический софизм?

Математический софизм — это ошибка в логике математического вычисления, которая приводит к неверному результату. Он может быть вызван неправильным пониманием математических понятий, неправильным применением математических операций или неверным логическим рассуждением.

Примером математического софизма может послужить ситуация, когда мы делаем ошибку в вычислениях, используя неправильный приоритет операций или не учитываем особенности математических функций. Это может привести к неверным результатам, которые могут повлиять на принятие важных решений в нашей жизни или работе.

Для того чтобы избежать математического софизма нужно четко понимать все математические понятия и уметь правильно применять математические операции. Также необходимо учитывать особенности каждой математической функции и следить за приоритетом операций при выполнении вычислений. И, конечно же, при любых вычислениях нужно быть внимательными и не допускать опечаток или прочих ошибок.

Примеры математических софизмов

1. Парадокс iPhone

Допустим, вы решили продать свой iPhone за 300 долларов с целью заработать на нем. Первый потенциальный покупатель предлагает вам купить его за 270 долларов, что вы соглашаетесь. Однако, следующий покупатель оказывается диктатором страны и предлагает вам купить iPhone за 30 долларов. Что вы выберете? Ваша интуиция может подсказать, что скорее всего вы выберете продать iPhone за 270 долларов и получить немедленную прибыль, однако, в этом случае вы теряете шанс продать свой iPhone за 300 долларов. Таким образом, более выгодным выбором будет продолжать поиски покупателя, даже если это может занять больше времени.

2. Парадокс Монти Холла

Вы участвуете в игре, в которой находятся три закрытых двери — за одной из них находится приз, за остальными двумя — ничего. Вы выбираете одну из дверей, но до открытия выигрышной двери ведущий открывает одну из оставшихся дверей, за которой находится ничего. Затем он предлагает вам выбор — остаться при своем выборе или перейти к другой неоткрытой двери. Вопрос — изменится ли вероятность выигрыша, если вы измените свой выбор? Несмотря на интуитивную логику, вероятность выигрыша увеличится, если вы измените свой выбор.

3. Парадокс Банаха-Тарского

Этот математический софизм сочетает в себе свойства теории множеств и теории групп. Суть его заключается в том, что сфера может быть разложена на конечное число частей, которые могут быть перегруппированы и преобразованы в две одинаковые сферы. Таким образом, можно утверждать, что одна сфера может быть удвоена путем преобразований и перегруппировок частей.

Вопрос-ответ:

Что такое математический софизм и как его распознать?

Математический софизм — это неверное умозаключение в математике или неправильное решение задачи. Распознать его можно путем анализа каждого шага в решении задачи или доказательства теоремы.

Какие ошибки являются наиболее распространенными в математике?

Наиболее распространенными ошибками в математике являются: неправильное применение формул, ошибки в вычислениях, неверная интерпретация данных задачи, неправильная постановка задачи. Однако, существует множество других ошибок, которые могут возникнуть в процессе решения математических задач.

Как избежать ошибок в вычислениях?

Чтобы избежать ошибок в вычислениях, необходимо внимательно читать условия задач, проверять правильность написания формул и действий. Перепроверять каждый шаг решения задачи и убедиться, что ответ корректен. Также полезно использовать калькулятор при выполнении математических вычислений.

Что делать, если я заметил ошибку в моем решении задачи?

Если вы заметили ошибку в вашем решении задачи, необходимо повторить все вычисления, перепроверить каждый шаг и найти место, где допущена ошибка. Если вы не можете найти ошибку, можно попросить друга или преподавателя проверить ваше решение. В некоторых случаях, может потребоваться решить задачу заново.

Каким образом математические софизмы могут повлиять на жизнь людей?

Математические софизмы могут повлиять на жизнь людей, если они применяются в финансовых расчетах, проектах строительства, науке и других областях, где точные вычисления являются основой. Неправильные расчеты могут привести к серьезным финансовым потерям, остановке проектов и проблемам в научной деятельности.

Какие методы можно использовать для решения математических задач?

Существует множество методов для решения математических задач, от классических до более сложных. Некоторые из них: алгоритм Евклида, метод Гаусса для решения систем линейных уравнений, дифференциальное и интегральное исчисление для решения задач физики и т.д.

Как важно знание математики в повседневной жизни?

Знание математики в повседневной жизни очень важно. Оно позволяет рассчитывать финансы, давать оценки вероятности различных событий, планировать расписание и временные ресурсы. Математика также является основой для многих других наук, таких как физика, химия, биология и т.д.

Утверждения, которые могут привести к ошибкам в вычислениях

Утверждение: В результате деления нуля на любое число получится ноль.

Пояснение: Это утверждение неверно, так как деление на ноль не определено и приведет к ошибке в вычислениях.

Утверждение: При вычислениях с дробями можно просто складывать или вычитать числители и знаменатели отдельно.

Пояснение: Это утверждение неверно, так как для правильных вычислений нужно сначала привести дроби к общему знаменателю, а затем только проводить операции с числителями.

Утверждение: При вычислениях с процентами можно просто умножать или делить числа на сто.

Пояснение: Это утверждение неверно, так как при вычислении процентов нужно учитывать базу, то есть из чего производится процентное вычисление. Также при выполнении последовательности операций с процентами нужно учитывать приоритетности операций.

• Утверждение: При расчете суммы чисел с плавающей точкой надо использовать метод округления в большую сторону.
• Пояснение: Это утверждение неверно, так как в зависимости от задачи может потребоваться использование других методов округления, например, округление в меньшую сторону или до ближайшего целого.

Превратности процента

Процент — одна из самых распространенных математических операций. Однако, несмотря на ее простоту, проценты могут стать источником ошибок в вычислениях, если не учитывать все их превратности.

Простейший пример — изменение стоимости товара на определенный процент. Допустим, товар стоит 100 рублей и его цена увеличивается на 20%. Какова будет новая цена товара? Многие думают, что нужно просто добавить 20 рублей и получится 120 рублей. Однако это неверно! Новая цена будет 120 рублей только если удовлетворены условия, что она увеличилась на 20% после первоначального увеличения на 20%. Для правильного расчета нужно учитывать, что увеличение должно быть произведено на сумму, полученную после первоначального увеличения, то есть на 120 рублей.

Кроме того, проценты могут иметь различные базы. Например, процентная ставка может быть указана относительно начальной суммы, или уже после предыдущих изменений. Нужно внимательно следить за условиями и правильно рассчитывать проценты, чтобы избежать ошибок в вычислениях.

Важно помнить также, что проценты могут быть добавлены или вычтены из числа, которое выражает не процент, а какую-либо физическую величину. Например, при расчете налогов или скидок на товары.

Иногда может быть полезно использовать таблицы процентов для упрощения вычислений. Однако, даже в этом случае необходимо убедиться в том, что таблица отражает все условия конкретной задачи.

Зачем нужно умение работать с процентами?

Умение работать с процентами является неотъемлемой частью математических навыков и важно как в повседневной жизни, так и в профессиональной сфере. Знание процентов позволяет быстро и легко рассчитывать различные величины, что является необходимым навыком в финансовой и экономической сферах, при планировании расходов, налоговых расчетов и инвестировании.

Также, умение работать с процентами пригодится в повседневной жизни. Например, при скидочных акциях в магазинах, расчетах сумм за услуги и товары, определении процента увеличения зарплаты и так далее.

Новичкам в финансовой сфере, особенно при работе с кредитами и долгами, необходимо умение правильно расчитывать проценты, чтобы избежать переплат и финансовых потерь. Для руководителя компании важно уметь рассчитывать проценты на вложенные средства, действующие акции, обязательства перед партнерами и так далее.

Таким образом, умение работать с процентами является важной составляющей математических навыков, которые необходимы как в повседневной жизни, так и в профессиональной сфере.

Как избежать ошибок в вычислениях с процентами?

Проценты – одна из наиболее распространенных математических концепций в повседневной жизни. Однако, если вы не знаете, как правильно вычислять проценты, можете совершить ошибки, которые могут стоить вам дорого.

Первый шаг для избежания ошибок в вычислениях с процентами – понимание формулы процентов. Используйте формулу процентов, чтобы рассчитать число, которое составляет определенный процент от другого числа. Например, формула для вычисления 25% от 100 – это 0,25 × 100 = 25.

Еще один способ избежать ошибок в вычислениях с процентами – использование калькулятора. Калькулятор может быть полезным инструментом при работе с процентами. Однако, не забывайте, что калькулятор не идеальный и может совершать ошибки, поэтому всегда проверяйте результаты.

Также не следует забывать, что при вычислениях с процентами нужно быть внимательным в отношении единиц измерения. Например, если вы вычисляете проценты на основе долларов США, убедитесь, что используете ту же самую валюту для всех чисел в вашем уравнении.

В заключение, избежать ошибок в вычислениях с процентами можно, если вы понимаете формулу процентов, используете калькулятор при необходимости и всегда следите за единицами измерения.

Как правильно округлять числа?

Округление чисел часто используется в математике и в программировании. Оно позволяет упростить числа и сделать их более читаемыми. Тем не менее, при округлении чисел можно совершить ошибки, которые могут привести к некорректным результатам.

Для правильного округления чисел нужно учитывать следующие правила:

• Если цифра, следующая за цифрой, которую нужно округлить, меньше 5, то число округляется до меньшего ближайшего целого числа.
• Если цифра, следующая за цифрой, которую нужно округлить, равна или больше 5, то число округляется до большего ближайшего целого числа.
• Если цифра, следующая за цифрой, которую нужно округлить, равна 5, то число округляется до ближайшего четного целого числа.

Например, число 2.43 нужно округлить до двух знаков после запятой. Так как цифра, следующая за 3, меньше 5, то число будет округлено до 2.43.

А если число 4.56 нужно округлить до двух знаков после запятой, то так как цифра, следующая за 5, больше или равна 5, то число будет округлено до 4.57.

Нужно также помнить о том, что существует несколько способов округления чисел, таких как округление до ближайшего целого, округление до наименьшего целого, округление до наибольшего целого и другие. Выбор способа должен зависеть от требований задачи и от правил округления, принятых в каждой конкретной области.

Правильно округляя числа, можно избежать ошибок и добиться более точных результатов в вычислениях.

Роль алгебры в исключении возможных ошибок

Алгебра — это один из фундаментальных разделов математики, который важен в повседневной жизни и научных исследованиях. Она не только помогает в решении различных процентных задач, но и может предотвратить возможные ошибки в вычислениях.

Алгебра позволяет записывать формулы и выражения в более удобном виде, а также систематизировать их. Это позволяет избежать ошибок, которые могут быть вызваны неточностями в записи или забытых действиях. Кроме того, алгебра обеспечивает системность в вычислениях, что также уменьшает вероятность ошибок.

При решении сложных математических задач, использование алгебры может существенно облегчить процесс решения. Следование строгим правилам алгебры помогает тщательно проверить каждый шаг вычисления, что, в свою очередь, способствует исключению возможных ошибок.

Кроме того, изучение алгебры требует от человека определенной дисциплины и точности. Эти качества могут быть полезными не только в математике, но и во многих других сферах жизни. Ответственное отношение к записям и вычислениям может помочь уменьшить ошибки и увеличить точность в любой деятельности, которая связана с использованием чисел.

Таким образом, алгебра играет важную роль в избежании возможных ошибок в математических вычислениях. Она предоставляет необходимые инструменты и знания для эффективного решения задач, уменьшая вероятность ошибок и повышая точность.

Правильное использование скобок в вычислениях

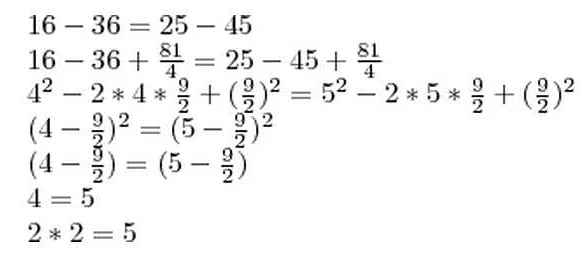
Правильное использование скобок в вычислениях помогает избежать ошибок и увеличивает точность расчетов. Скобки нужны для задания порядка выполнения операций и определения приоритета вычислений.

В математике существует несколько типов скобок: круглые (), квадратные [] и фигурные {}. Круглые скобки используются для группировки арифметических операций и определения приоритета вычислений. Если в выражении есть скобки разных типов, то всегда сначала выполняются операции внутри скобок наиболее высокого приоритета.

Важно помнить, что если знаков умножения или деления нет между числами и скобками, то подразумевается, что они умножаются. Например, выражение 2(3+4) будет интерпретироваться как 2*(3+4), а не 2*3+4.

Еще одна распространенная ошибка при использовании скобок — неправильное количество скобок. Необходимо всегда следить за тем, чтобы число открывающих скобок было равно числу закрывающих. Лишняя скобка или ее отсутствие может полностью изменить значение выражения.

В таблице ниже приведен пример порядка выполнения операций:

ОперацияПриоритет

Круглые скобки ( )	Наивысший
Степень ( ^ )	Высокий
Умножение ( * ) и деление ( / )	Средний
Сложение ( + ) и вычитание ( — )	Низкий

Правильное использование скобок помогает избежать ошибок и повышает точность расчетов.

Как избежать ошибок в вычислениях при применении формул и уравнений?

Правильное применение формул и уравнений в математике может быть сложным и затруднительным для многих людей. Ошибки в вычислениях могут привести к неверным ответам и неправильным решениям задач. Чтобы избежать таких ошибок, нужно соблюдать несколько простых правил.

1. Проверяйте правильность записи уравнений и формул. Перепроверьте каждый символ и каждую операцию, чтобы убедиться, что все написано правильно.
2. Понимайте, что означают все символы и знаки. Не используйте формулы, которые не понимаете. Прочитайте определения всех переменных и знаков и объяснения их взаимодействия, если это необходимо.
3. Используйте правильные единицы измерения. Убедитесь, что все входящие в формулу значения имеют одинаковые единицы измерения.
4. Проверьте, что все данные точны и полны. Не используйте округленные значения, если это непринципиально. Убедитесь, что в формулу включены все необходимые значения.
5. Используйте калькулятор или компьютерную программу для сложных вычислений. Если у вас не хватает навыков в ручном вычислении или формула слишком сложная, используйте электронный калькулятор или специальную программу.

Перепроверьте свои результаты, чтобы убедиться в их правильности. Математические ошибки могут привести к дополнительной работе, проблемам при решении задач и стрессу. Но если вы следуете простым правилам и методам, вы можете сократить риск ошибок и получить правильный результат.

Резюме

Математический софизм представляет собой логическую ошибку, совершаемую в процессе выполнения математических вычислений. Избежать ошибок в вычислениях можно путем тщательной проверки каждого шага и использования правильных математических формул.

Особое внимание следует уделить проблемам округления и масштабирования чисел, которые могут привести к значительным ошибкам в вычислениях. Для решения таких проблем необходимо использовать специализированные алгоритмы и библиотеки, а также строго следить за последовательностью вычислений.

Кроме того, важно не забывать о правилах алгебры и геометрии при решении задач, а также о возможных логических ловушках. При выполнении математических вычислений необходимо проявлять внимательность, терпение и дисциплину, чтобы избежать ошибок и достичь требуемых результатов.