Что значит округлить по правилам математического округления

Математическое округление — это процесс приведения числа к ближайшему целому значению с учетом определенных правил. Узнайте, какие правила используются при округлении чисел и как применять их в практике.

Округление чисел является важной операцией в математике и программировании. Верное округление чисел обеспечивает точность вычислений и результатов, а также упрощает их понимание и интерпретацию. Округление выполняется в соответствии с определенными правилами, которые могут отличаться в разных странах и сферах применения.

Одним из наиболее распространенных правил округления является математическое правило. Согласно ему, число округляется до ближайшего целого числа. Если дробная часть числа равна 0,5, то число округляется до ближайшего четного целого числа. Например, число 2,5 будет округлено до 2, а число 3,5 будет округлено до 4.

Округление в соответствии с математическим правилом обеспечивает справедливое и равномерное распределение округленных значений вокруг исходного числа.

Кроме математического правила, существуют и другие правила округления, такие как правило округления вниз, правило округления вверх и правило округления к нулю. Каждое из этих правил имеет свои особенности и применение в различных сферах, включая бухгалтерию, финансы, статистику и др.

Важно помнить, что правила округления могут варьироваться в зависимости от контекста и требований конкретной задачи или методики. Поэтому перед округлением чисел необходимо учитывать эти особенности и выбирать соответствующее правило округления для достижения требуемой точности и результатов.

Округление чисел: что это такое?

Для округления чисел существуют разные математические правила, которые определяют, к какому целому числу должно быть округлено число.

Наиболее распространенные правила округления:

Правило округленияОписание

Математическое округление	Число округляется к ближайшему целому числу. Если дробная часть числа равна 0.5, то число округляется в сторону четного целого числа.
Округление вниз	Число округляется к наименьшему целому числу, которое не превышает исходное число.
Округление вверх	Число округляется к наибольшему целому числу, которое не меньше исходного числа.
Округление к нулю	Число округляется к нулю, если оно положительное, и к нулю с обратным знаком, если оно отрицательное.

Выбор правила округления зависит от конкретной задачи и требований к точности чисел. Правильное округление чисел позволяет получить более удобочитаемые и точные результаты при выполнении математических операций.

Важно помнить, что округление чисел может привести к потере точности, особенно при работе с большими числами или при выполнении сложных манипуляций с десятичными дробями. Поэтому при необходимости с высокой точностью округления следует использовать специальные алгоритмы и библиотеки.

Числа и десятичные разряды

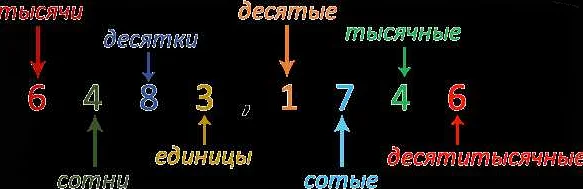
В десятичной системе счисления каждое число имеет определенное количество десятичных разрядов, которые идут после запятой. Например, число 3.14159 имеет пять десятичных разрядов, а число 10.0 имеет один десятичный разряд.

При округлении чисел с десятичными разрядами следует обратить внимание на следующие правила:

• Если десятичный разряд равен 5, то следует округлить цифру в десятичном разряде до ближайшего четного значения. Например, число 3.5 округляется до 4, а число 4.5 округляется до 4.
• Если десятичный разряд меньше 5, то все цифры после него просто обрасываются. Например, число 3.14159 после округления до двух десятичных разрядов будет равно 3.14.
• Если десятичный разряд больше 5, то следует округлить цифру в десятичном разряде вверх. Например, число 3.9 округляется до 4, а число 4.6 округляется до 5.

Учет десятичных разрядов при округлении чисел позволяет сохранить точность вычислений и избежать ошибок при округлении.

Округление до ближайшего целого числа

Для выполнения округления до ближайшего целого числа в языке программирования можно использовать функцию round(). Например, если у нас есть число 3.7, то при использовании функции round() оно будет округлено до 4, так как десятичная часть (0.7) больше или равна 0.5.

Пример кода на языке Python:

x = 3.7
rounded_x = round(x)
print(rounded_x) # Вывод: 4

Однако стоит учитывать, что при округлении до ближайшего целого числа есть некоторые особенности. Например, если у нас есть число -2.5, то оно будет округлено до -2, так как десятичная часть (0.5) меньше 0.5. То есть, при округлении до ближайшего целого числа, положительные числа округляются в большую сторону, а отрицательные — в меньшую сторону.

Следует также отметить, что при использовании функции round() возможны небольшие погрешности. Например, если у нас есть число 2.5, то оно будет округлено в большую сторону до 3. Это связано с тем, что десятичная часть (0.5) больше или равна 0.5, и округление происходит в сторону положительной бесконечности.

Таким образом, округление до ближайшего целого числа является простым способом округления чисел, который используется во многих областях, особенно в программировании и математике.

Округление до заданной точности

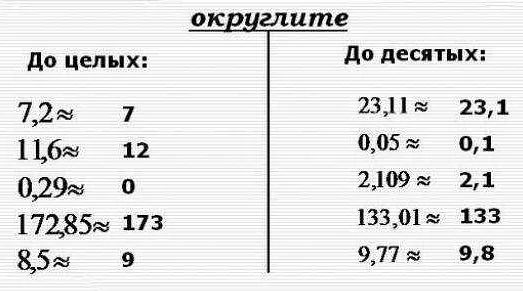
Для округления чисел в JavaScript используются различные методы. Один из них — метод toFixed(), который позволяет округлить число до определенного количества знаков после запятой. Например, если мы хотим округлить число 3.14159 до двух знаков после запятой, мы можем использовать следующий код:

let number = 3.14159;
let roundedNumber = number.toFixed(2);
console.log(roundedNumber); // Выведет «3.14»

Если нам необходимо округлить число до ближайшего целого значения, мы можем использовать методы Math.round(), Math.floor() и Math.ceil(). Метод Math.round() округляет число до ближайшего целого значения. Метод Math.floor() округляет число вниз до ближайшего меньшего целого значения, а метод Math.ceil() округляет число вверх до ближайшего большего целого значения.

let number = 3.7;
let roundedNumber = Math.round(number);
console.log(roundedNumber); // Выведет «4»
let flooredNumber = Math.floor(number);
console.log(flooredNumber); // Выведет «3»
let ceiledNumber = Math.ceil(number);
console.log(ceiledNumber); // Выведет «4»

Используя эти методы, мы можем производить округление чисел до заданной точности в соответствии с математическими правилами.

Округление в большую сторону

Для округления числа в большую сторону в программировании часто используется функция ceil(). Эта функция возвращает наименьшее целое число, которое больше или равно указанному числу. Например, ceil(3.6) вернет 4, а ceil(7.2) вернет 8.

Округление в большую сторону может быть полезно, когда необходимо получить наибольшее значение из числового ряда или произвести округление вверх для точного расчета.

Исходное числоОкругление в большую сторону

3.1	4
6.5	7
9.9	10

Округление в меньшую сторону

Например, если мы округляем число 3.8 в меньшую сторону до целого числа, то получим число 3. В данном случае, все десятичные знаки справа от точки (8) отбрасываются.

Округление в меньшую сторону также может применяться для округления до определенного количества знаков после запятой. Например, если мы округляем число 3.876 до двух знаков после запятой в меньшую сторону, то получим число 3.87. В данном случае, число 6, следующее за знаком запятой, отбрасывается.

Округление в меньшую сторону может быть полезно, когда требуется учитывать только целые числа или когда точность значения после запятой не является критически важной.

Однако, следует учитывать, что округление в меньшую сторону может приводить к потере точности и может не подходить для некоторых операций, требующих более точных результатов.

Округление к ближайшему четному числу

Примеры округления к ближайшему четному числу:

• Округление числа 3 к ближайшему четному числу даст число 2, так как 2 — это ближайшее меньшее четное число.
• Округление числа 6 к ближайшему четному числу не требуется, так как 6 уже является четным числом.
• Округление числа 5 к ближайшему четному числу даст число 4, так как 4 — это ближайшее меньшее четное число.

Округление к ближайшему четному числу может быть полезным при работе с данными, когда необходимо упростить числовую информацию и сделать ее более понятной и удобной для анализа.

Видео по теме:

Вопрос-ответ:

Как правильно округлять числа?

Округление чисел следует проводить в соответствии с математическими правилами, при которых число округляется до ближайшего целого числа. Если десятичная часть числа больше или равна 0.5, то число округляется в большую сторону. Если десятичная часть числа меньше 0.5, то число округляется в меньшую сторону.

Как округлить число до ближайшего целого?

Чтобы округлить число до ближайшего целого, нужно посмотреть на его десятичную часть. Если эта часть больше или равна 0.5, то число округляется в большую сторону, добавляя 1 к целой части. Если десятичная часть меньше 0.5, то число округляется в меньшую сторону, просто отбрасывая десятичную часть.

Как округлить число до определенного количества знаков после запятой?

Чтобы округлить число до определенного количества знаков после запятой, нужно определить степень округления. Если следующая цифра после указанного количества знаков равна или больше 5, то число округляется в большую сторону, добавляя 1 к последней цифре. Если следующая цифра меньше 5, то число округляется в меньшую сторону, просто отбрасывая оставшиеся цифры.

Как округлить число до ближайшей десятой, сотой или тысячной?

Для округления числа до ближайшей десятой, сотой или тысячной нужно определить степень округления. Если следующая цифра после указанной степени округления равна или больше 5, то число округляется в большую сторону, добавляя 1 к указанной степени округления. Если следующая цифра меньше 5, то число округляется в меньшую сторону, просто отбрасывая оставшиеся цифры после указанной степени округления.

Что такое округление вверх и вниз?

Округление вверх — это когда число округляется до ближайшего большего целого числа. Округление вниз — это когда число округляется до ближайшего меньшего целого числа. Например, число 4.6 при округлении вверх станет 5, а при округлении вниз — 4.

Округление к ближайшему нечетному числу

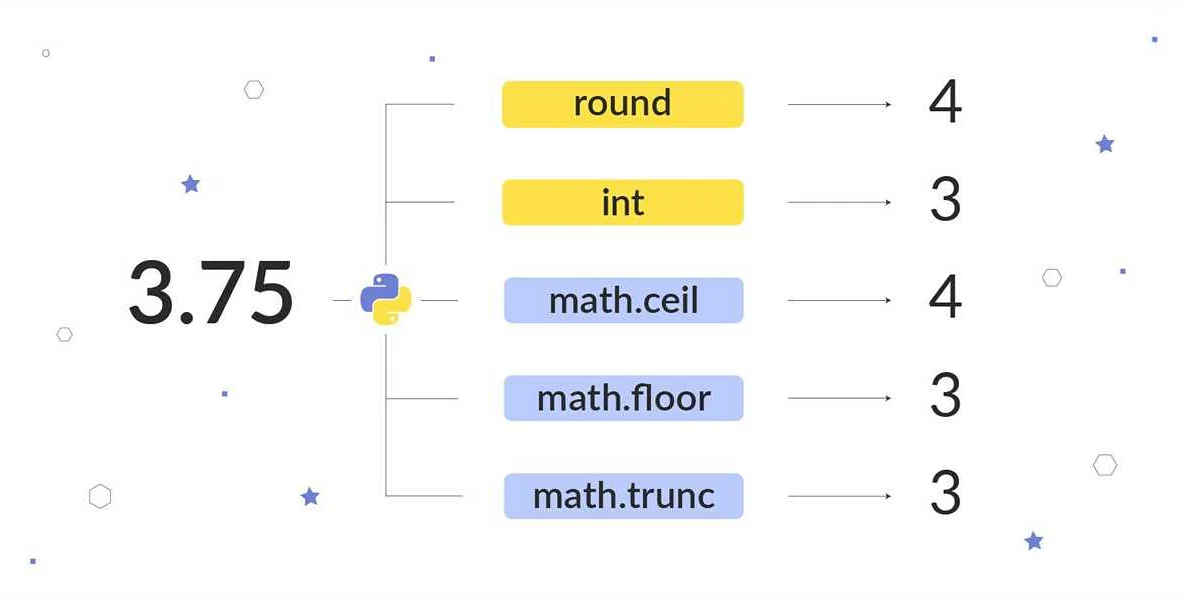
Правило округления к ближайшему нечетному числу состоит в следующем:

1. Если исходное число является нечетным, то оно остается неизменным.

2. Если исходное число является четным, то оно округляется до ближайшего нечетного числа. Если два нечетных числа равноудалены от четного числа, то округление происходит в сторону большего значения.

Для лучшего понимания правила округления к ближайшему нечетному числу, можно рассмотреть примеры:

Исходное числоОкругленное нечетное число

1.5	1
2.6	3
4.2	5
7.9	7

Таким образом, правило округления к ближайшему нечетному числу позволяет получить результат, более точно соответствующий исходному числу и учитывающий его четность.

Примеры округления чисел

Рассмотрим несколько примеров округления чисел:

Пример 1: Округление числа 3.45 по математическим правилам до двух десятичных разрядов.

Результат: 3.45 округляется до 3.45, так как третий десятичный разряд (5) не требует изменения предыдущего разряда.

Пример 2: Округление числа 7.89 по правилам большинства до одного десятичного разряда.

Результат: 7.89 округляется до 7.9, так как второй десятичный разряд (9) больше или равен 5, что приводит к увеличению предыдущего разряда на 1.

Пример 3: Округление числа 12.34 по правилам банковского округления до целого числа.

Результат: 12.34 округляется до 12, так как десятые и сотые десятичные разряды (3 и 4) не требуют изменения предыдущего разряда.

Это лишь несколько примеров округления чисел, и существуют и другие правила и методы округления чисел. Важно понимать правила округления и применять их в соответствии с требованиями и контекстом задачи.