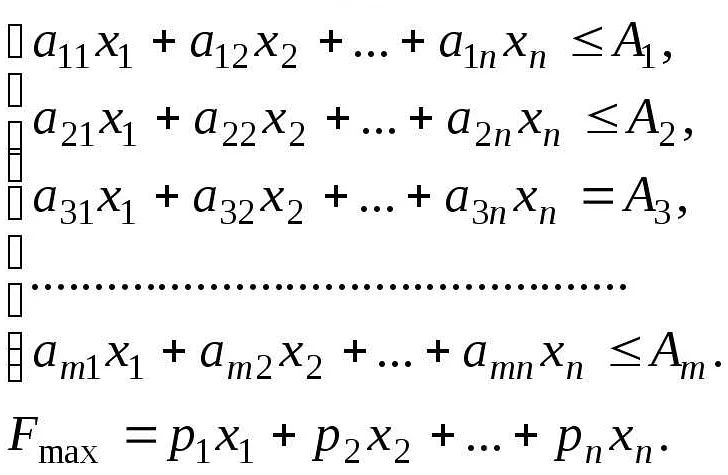Оптимальное решение экономико-математической задачи: как достичь максимальной эффективности

Оптимальное решение экономико-математической задачи – это решение, которое при условии наложения ограничений и учета всех факторов приводит к максимизации или минимизации искомой величины. В статье мы расскажем, как достичь оптимального решения и какие методы могут помочь в этом.

Экономико-математические задачи – это задачи, в которых рассматриваются экономические процессы с помощью математических методов. Одна из важных частей решения таких задач – это поиск оптимального решения. Оптимальное решение – это решение, которое максимизирует или минимизирует функционал, на основе которого составляется условие задачи.

Поиск оптимального решения может быть выполнен с помощью различных методов. Одним из наиболее распространенных методов является метод линейного программирования. С его помощью можно решать задачи, в которых требуется спланировать оптимальное использование ресурсов при наличии ограничений. Однако, в зависимости от условий задачи, могут применяться и другие методы, такие как методы динамического программирования, методы оптимизации функций нескольких переменных и др.

Важно отметить, что поиск оптимального решения экономико-математической задачи является важным инструментом для принятия правильных решений и повышения эффективности бизнес-процессов. Поэтому, знание основных методов решения таких задач является необходимым для специалистов в области экономики и управления.

Оптимальное решение экономико-математической задачи

Оптимальное решение экономико-математической задачи — это решение, которое обеспечивает минимальные затраты при максимальном выигрыше. Для того, чтобы найти оптимальное решение, необходимо провести анализ всех возможных вариантов и выбрать наилучший из них.

Для этого часто используются различные методы оптимизации, которые позволяют найти решение с минимальными затратами и максимальным выигрышем. Среди таких методов можно выделить методы линейного программирования, динамического программирования, а также различные случаи задачи оптимизации.

Оптимальное решение экономико-математической задачи позволяет значительно увеличить эффективность решения задачи и снизить затраты на ее выполнение. Поэтому, в современном бизнесе таких задач можно встретить очень много, а специалисты, которые умеют находить оптимальные решения, всегда востребованы и ценятся высоко.

Видео по теме:

Что такое экономико-математическая задача?

Экономико-математическая задача – это задача, которая часто возникает в экономике и финансах, и которая может быть решена с помощью методов математики. Она может иметь различные формы – от оптимизационных задач до задач принятия решений. Целью решения таких задач является получение оптимальных результатов и выбор наилучших решений, что позволяет экономить время и ресурсы.

Для решения экономико-математических задач используются различные методы математического моделирования. Они позволяют проанализировать данные, описывающие естественные или социальные явления, а затем найти оптимальное решение на основе заданных условий. Это могут быть задачи оптимизации, теории игр, прогнозирования и многие другие.

Важно понимать, что экономико-математическая задача является неотъемлемой частью современной экономики, и ее решение может оказывать огромное влияние на экономические процессы и принятие решений бизнеса. Поэтому эти задачи активно изучаются и развиваются, чтобы помочь в принятии наилучших решений и достижении успеха в экономической деятельности.

Как найти оптимальное решение задачи?

Найти оптимальное решение задачи – это процесс максимального удовлетворения стоящей перед вами задачи, учитывая ограничения и условия. Этот процесс может быть достигнут путем использования экономико-математических методов и моделей.

Для начала необходимо выделить и определить целевую функцию и ее условия. Затем можно начинать работу над математической моделью, которую можно сделать в виде уравнений и неравенств. Такой подход позволяет сократить количество бездумных попыток решения задачи, и сосредоточиться на адекватных и необходимых решениях.

Для поиска оптимального решения также можно использовать методы линейного и динамического программирования или оптимизации, которые позволяют достичь наибольшей эффективности в решении задач. Имеет смысл также проверять решения с помощью специального программного обеспечения и полезной информации, которая содержится в научных статьях и книгах.

Результатом всех этих действий и алгоритмов может быть только одно – оптимальное решение, которое обеспечит наибольшую реализацию задачи при минимальных затратах ресурсов. Знание и применение экономико-математических методов и моделей может помочь вам стать лидером в вашей отрасли и достичь высот успеха вам или вашей компании.

Вопрос-ответ:

Что такое экономико-математическая задача?

Экономико-математическая задача — это задача, которая решается с помощью математических методов в экономических целях. Она может быть связана с оптимизацией процессов, прогнозированием тенденций и т.д.

Как найти оптимальное решение экономико-математической задачи?

Для нахождения оптимального решения экономико-математической задачи используются математические методы. Один из них — это метод линейного программирования. С его помощью можно найти оптимальное решение задачи, учитывая различные ограничения и условия. Также можно использовать другие методы, такие как динамическое программирование, теория игр и т.д.

Какие данные нужны для решения экономико-математической задачи?

Для решения экономико-математической задачи необходимо иметь определенный набор данных. В зависимости от задачи это могут быть данные о ценах на товары, ограничения на доступные ресурсы, условия рынка и т.д. Чтобы эффективно решить задачу, важно правильно выбрать данные и подобрать подходящий метод.

Как проверить корректность решения экономико-математической задачи?

Для проверки корректности решения экономико-математической задачи можно использовать различные методы. Один из них — это метод чувствительности. Он позволяет оценить, как изменение параметров в задаче повлияет на решение. Также можно провести анализ диапазона допустимых значений или сравнить полученное решение с результатами других методов.

Какие ограничения могут быть у экономико-математической задачи?

Ограничения экономико-математической задачи могут быть различными. Например, задача может быть ограничена доступностью определенных ресурсов, правилами рынка, налоговыми законами и т.д. Ограничения могут быть как жесткими, так и мягкими, и их необходимо учитывать при выборе метода решения задачи.

Какие проблемы могут возникнуть при решении экономико-математической задачи?

При решении экономико-математической задачи могут возникать различные проблемы. Одна из них — это наличие неопределенности в данных, которая может привести к неправильному решению задачи. Также могут возникать проблемы с выбором подходящего метода, неправильным учетом ограничений или недостаточной точностью вычислений. Важно следить за качеством данных и выбирать подходящие методы решения задачи.

Можно ли применять методы математического моделирования к неэкономическим задачам?

Да, методы математического моделирования можно применять к различным задачам, не только экономическим. Они могут быть полезны в науке, производстве, физике и т.д. Например, научные исследователи могут использовать методы моделирования для прогнозирования погоды или изучения свойств материалов. Однако при применении методов необходимо учитывать особенности задачи и выбирать подходящие методы решения.

Какие методы используются для поиска оптимального решения?

В экономико-математических задачах для поиска оптимального решения используются различные методы. Некоторые из них:

• Метод Лагранжа — используется для поиска условного экстремума функции при заданных ограничениях. Этот метод позволяет свести задачу к обычной задаче без ограничений, что упрощает ее решение.
• Симплекс-метод — используется для решения задач линейного программирования, то есть задач оптимизации линейной функции при линейных ограничениях.
• Метод динамического программирования — применяется для задач оптимизации, связанных с некоторыми последовательностями действий. Этот метод основан на разбиении задачи на более простые подзадачи, и решении их в порядке возрастания сложности.

Кроме того, существуют методы многокритериальной оптимизации, которые позволяют решать задачи с несколькими целями одновременно. В этом случае поиск оптимального решения сводится к поиску компромиссного решения, которое удовлетворяет всем целям в наилучшей возможной степени.

Выбор метода для решения оптимизационной задачи зависит от ее типа, сложности и количества ограничений. Для каждой задачи необходимо выбрать наиболее подходящий метод, который обеспечит нахождение оптимального решения.

Метод Лагранжа: что это такое?

Метод Лагранжа — это один из методов решения экономико-математических задач, который использует уравнения Лагранжа для нахождения условного экстремума функции. Этот метод был разработан итальянским математиком Жозефом Луи Лагранжем в 18 веке.

Уравнения Лагранжа используются для нахождения максимума или минимума функции, учитывая определенные ограничения. К примеру, если требуется найти точку на функции, которая удовлетворяет условию, что определенные переменные должны быть равны или принимать определенные значения, то можно использовать метод Лагранжа.

Метод Лагранжа используется в различных областях, включая экономику, физику, химию и технические науки. Он позволяет оптимизировать функции, которые находятся под ограничениями, что часто встречается в прикладных задачах.

В общем случае, метод Лагранжа заключается в составлении системы уравнений, где каждое уравнение — это производная функции Лагранжа по каждой переменной, умноженная на множитель Лагранжа. После решения системы уравнений можно найти точки максимума или минимума функции.

Метод Лагранжа широко используется в экономико-математических задачах и помогает найти оптимальное решение при ограничениях на переменные. Этот метод особенно полезен в экономике, где многие задачи связаны с ограничениями на объем производства, ресурсы и другие переменные.

Как применить метод Лагранжа для решения экономико-математической задачи?

Метод Лагранжа является одним из способов решения экономико-математических задач. Этот метод основан на принципе максимума или минимума функции с ограничениями. Изначально, задача формулируется в виде функции, которую необходимо максимизировать или минимизировать, при этом указываются ограничения на переменные.

Для применения метода Лагранжа необходимо создать функцию Лагранжа, которая состоит из исходной функции и умноженной на множитель Лагранжа, который определяется ограничениями на переменные. Затем, необходимо произвести частные производные функции Лагранжа по всем переменным и приравнять их к нулю. Получившиеся уравнения решаются относительно переменных.

После нахождения решений переменных, необходимо проверить, что найденное решение является минимумом или максимумом функции с учетом ограничений, указанных в исходной задаче. Если найденное решение удовлетворяет ограничениям и является минимумом или максимумом функции, то это оптимальное решение задачи.

Метод Лагранжа является эффективным способом решения экономико-математических задач, особенно в случаях, когда необходимо учитывать ограничения на переменные. Но для его применения необходимо иметь хорошее математическое образование и навыки работы с уравнениями и производными.

Метод множителей Лагранжа: обзор метода

Метод множителей Лагранжа – это метод нахождения условного экстремума функции многих переменных. Он был разработан итальянским математиком Лагранжем в XVIII веке и является одним из самых распространенных методов оптимизации.

Суть метода заключается в следующем: если задана функция f(x1, x2, …, xn), которую нужно оптимизировать при условии g(x1, x2, …, xn) = 0, то метод множителей Лагранжа заключается в нахождении таких чисел λ1, λ2, …, λm, что функция

L(x1, x2, …, xn, λ1, λ2, …, λm) = f(x1, x2, …, xn) + λg(x1, x2, …, xn)

дает экстремум при любом (x1, x2, …, xn), удовлетворяющем условию g(x1, x2, …, xn) = 0. То есть решение задачи сводится к нахождению экстремума функции L(x1, x2, …, xn, λ1, λ2, …, λm) по всем переменным.

Преимуществом метода множителей Лагранжа является простота вычисления, возможность применения для задач с произвольным числом ограничений и возможность обобщения на случай неравенств в качестве условий.

Однако недостатком метода является наличие ложных экстремумов и необходимость проверки их корректности. Также некоторые задачи могут не иметь решений при использовании метода множителей Лагранжа.

Тем не менее, метод множителей Лагранжа продолжает оставаться одним из самых важных инструментов оптимизации и находит применение в различных областях, включая экономику, физику, инженерию и другие.

Как применить метод множителей Лагранжа для решения задачи максимума и минимума?

Метод множителей Лагранжа — это метод решения экономико-математических задач на поиск максимума и минимума функций с ограничениями.

Для применения метода множителей Лагранжа необходимо сформулировать функцию, которую нужно максимизировать или минимизировать, а также функцию-ограничение. Далее необходимо составить функцию Лагранжа, добавив к исходной функции произведение множителя Лагранжа и функции-ограничения.

Далее необходимо найти экстремум функции Лагранжа, то есть найти значения переменных функций, при которых функция Лагранжа принимает экстремальное значение.

Чтобы найти такие значения, необходимо решить систему уравнений, которые составляются из производных функции Лагранжа по переменным и функции-ограничения. Полученные значения подставляются в функцию Лагранжа, которая даст искомый максимум или минимум для исходной функции.

Метод множителей Лагранжа является эффективным средством решения задач на поиск максимума и минимума функций с ограничениями и широко применяется в экономических и финансовых исследованиях.

Метод симплекс: что это такое и когда его используют?

Метод симплекс — один из основных методов решения линейных программирования, используемый для поиска оптимального решения экономико-математических задач. Его основная задача заключается в том, чтобы найти такое значение переменных, которые обеспечивают наилучший результат функции, при условии выполнения заданных ограничений.

Метод симплекс используется в тех случаях, когда количество переменных ограничено, и часто применяется в экономической и промышленной сфере. Например, он может использоваться для оптимизации производства или распределения ресурсов между различными проектами

Основное преимущество метода симплекс заключается в его эффективности. Он позволяет получить быстрый и точный результат даже при комплексных условиях. При этом, если задача имеет множество решений, метод симплекс может помочь найти все оптимальные варианты

Для использования метода симплекс необходимо предварительно сформировать матрицу коэффициентов, которая включает в себя все данные, необходимые для решения задачи. Затем выполняются ряд шагов, включающих в себя пересчет значений переменных и учет ограничений, чтобы найти оптимальный результат функции.

Что такое целочисленное линейное программирование?

Целочисленное линейное программирование (ЦЛП) — это специальный вид линейного программирования, где все или некоторые переменные являются целыми числами, в отличие от обычного линейного программирования, где переменные могут быть любыми действительными числами.

В задачах ЦЛП, дополнительное требование целочисленности изменяет структуру оптимального решения, и может приводить к различного рода сложностям в поиске оптимального решения. Несмотря на это, ЦЛП используется широко в экономике, финансах, логистике и других областях для моделирования условий реальных задач.

ЦЛП может быть решена с помощью различных методов, таких как полный перебор, метод ветвей и границ, метод симплекс, метод динамического программирования и др. Одним из наиболее эффективных методов для решения ЦЛП является метод ветвей и границ, который основан на разбиении множества допустимых решений на подмножества и последующем их анализе.

• Преимущества использования ЦЛП:
  • Возможность учета дополнительных ограничений, связанных с целочисленными значениями переменных;
  • Понимание структуры оптимального решения, которое может быть полезно для принятия решений;
• Недостатки использования ЦЛП:
  • Сложность решения задач в связи с дополнительным требованием целочисленности переменных;
  • Ограничения по количеству переменных в задаче, что ограничивает его применение в некоторых случаях;

Какие методы решения задач целочисленного линейного программирования существуют?

Одним из методов решения задач целочисленного линейного программирования является метод перебора, также называемый полным перебором или методом ветвей и границ. Данный метод заключается в том, чтобы систематически перебирать все возможные варианты решения задачи, начиная со случая минимального значения функции целей.

Еще одним методом решения задач целочисленного линейного программирования является метод декомпозиции. Данный метод заключается в разбиении задачи на несколько подзадач, которые затем решаются отдельно. Решения подзадач затем комбинируются, чтобы получить общее оптимальное решение.

Также существуют эвристические методы решения задач целочисленного линейного программирования, которые основаны на применении определенных эвристических правил. При этом может быть нарушено условие точности решения, однако полученное решение будет оптимальным с определенной точностью.

Методы решения задач целочисленного линейного программирования используются в экономике, производственном управлении, логистике, математическом моделировании и других областях.

Как выбрать подходящий метод для решения экономико-математической задачи?

Решение экономико-математической задачи — это процесс принятия оптимального решения на основе математических моделей и теоретических методов. Однако, выбрать подходящий метод для решения задачи не всегда просто. Необходимо учитывать характеристики задачи, доступную информацию, а также свои навыки и опыт.

Определите цель решения задачи. Прежде чем выбрать метод, определите, что именно вы хотите достичь решением задачи. Цель может быть максимизация прибыли, минимизация издержек, нахождение оптимального выбора и т.д. Задачи также могут быть классифицированы как статические или динамические.

Оцените данные и параметры задачи. После определения цели, необходимо оценить доступную информацию. Какие данные вам нужны для решения задачи? Какие ограничения и условия присутствуют в задаче? Какие параметры следует учитывать?

Изучите доступные методы решения. В зависимости от задачи и характеристик данных, может быть применено несколько методов решения. Некоторые из них включают линейное программирование, динамическое программирование, теорию игр, матричные методы, регрессионный анализ и многие другие. Изучите каждый метод, его преимущества и недостатки, а также условия его использования.

Выберите подходящий метод. После тщательного изучения доступных методов решения и характеристик задачи, выберите метод, который наиболее эффективен и подходит для вашей цели. Обратите внимание на необходимые навыки и компетенции для применения выбранного метода.

Проверьте полученное решение. После получения результата, проверьте его на адекватность и соответствие цели решения задачи. Если результат не соответствует требованиям, необходимо повторить процесс с использованием другого метода или уточнением данных.