Экономико математические задачи цель которых состоит в нахождении наилучшего с точки зрения
Содержимое
- 1 Экономико математические задачи цель которых состоит в нахождении наилучшего с точки зрения
- 1.1 Экономико-математические задачи: нахождение наилучшего решения
- 1.2 Методы математического моделирования
- 1.3 Оптимизация в экономическом анализе
- 1.4 Анализ экономической эффективности
- 1.5 Применение линейного программирования
- 1.6 Методы динамического программирования
- 1.7 Видео по теме:
- 1.8 Вопрос-ответ:
- 1.8.0.1 Какие экономико-математические задачи можно решить с помощью нахождения наилучшего решения с точки зрения экономической эффективности?
- 1.8.0.2 Какие методы и модели используются для решения экономико-математических задач нахождения наилучшего решения?
- 1.8.0.3 Какие факторы учитываются при определении наилучшего решения в экономико-математических задачах?
- 1.8.0.4 Каким образом экономико-математические задачи нахождения наилучшего решения могут помочь предприятиям и организациям?
- 1.8.0.5 Каковы преимущества использования экономико-математических методов в решении задач нахождения наилучшего решения?
- 1.9 Моделирование риска и неопределенности
- 1.10 Многокритериальная оптимизация
Экономико-математические задачи направлены на нахождение наилучших решений с точки зрения экономической эффективности, оптимальности и максимизации выгоды. Используя математические методы и модели, эти задачи помогают определить оптимальные стратегии и принять решения, основанные на научных данных и анализе. Знание экономической теории и математических методов позволяет решать сложные экономические задачи и оптимизировать различные процессы в бизнесе, финансах и других сферах деятельности.
Экономико-математические задачи имеют особое значение в различных сферах экономики, где необходимо принимать решения с точки зрения экономической эффективности. В таких задачах математические методы и модели используются для определения наилучшего решения, которое позволит достичь максимальной прибыли или минимизировать затраты.
Одной из основных задач экономико-математического анализа является задача оптимизации. В рамках этой задачи необходимо найти такие значения переменных, при которых достигается максимальное или минимальное значение функции, представляющей собой эффективность решения. Для решения данной задачи применяются различные методы, такие как линейное программирование, динамическое программирование и теория игр.
Важной составляющей экономико-математических задач является анализ чувствительности. После нахождения наилучшего решения необходимо оценить его устойчивость к изменениям параметров. Анализ чувствительности позволяет оценить, насколько изменение значений параметров влияет на оптимальное решение и экономическую эффективность. Такой анализ позволяет принимать более обоснованные решения и учитывать возможные изменения во внешней среде.
Экономико-математические задачи позволяют компаниям и организациям принимать обоснованные решения с точки зрения экономической эффективности. При правильном использовании математических методов и моделей можно достичь оптимального баланса между прибылью и затратами, увеличить эффективность производства и улучшить конкурентоспособность на рынке.
В данной статье будут рассмотрены основные подходы и методы решения экономико-математических задач, их применимость в различных сферах экономики и примеры использования. Также будет дан обзор современных инструментов и программного обеспечения, которые помогают решать подобные задачи. Понимание и применение экономико-математических методов и моделей являются важными навыками для специалистов в области экономики и менеджмента, и данная статья поможет разобраться в основных принципах и инструментах для их решения.
Экономико-математические задачи: нахождение наилучшего решения

Нахождение наилучшего решения в экономико-математических задачах связано с определением оптимальных значений переменных и параметров в условиях ограничений и целевой функции. Часто используются различные методы оптимизации, такие как линейное программирование, нелинейное программирование, динамическое программирование и другие.
Для решения экономических задач необходимы не только математические знания, но и экономическая осведомленность. Важно уметь формализовать экономическую ситуацию, определить цели и ограничения, выбрать подходящую модель и метод решения.
При нахождении наилучшего решения в экономико-математических задачах, необходимо учитывать как экономические, так и математические аспекты. Важно учитывать реальные условия и ограничения, а также возможные риски и неопределенности.
Применение экономико-математических методов позволяет решать широкий спектр задач, таких как оптимизация производства, распределение ресурсов, инвестиционные решения, определение цен и многое другое. Это помогает компаниям и организациям принимать обоснованные и эффективные решения, основанные на математических моделях и анализе данных.
В итоге, экономико-математические задачи и методы являются важным инструментом для принятия решений в экономике. Они позволяют оптимизировать различные показатели и найти наилучшее решение с точки зрения экономической эффективности, учитывая все необходимые ограничения и риски.
Методы математического моделирования

Существует несколько основных методов математического моделирования в экономике:
- Линейное программирование: это метод моделирования, который позволяет найти оптимальное решение для задачи с линейной целевой функцией и линейными ограничениями. Он часто используется для оптимизации производственных процессов или распределения ресурсов.
- Динамическое программирование: этот метод моделирования позволяет найти оптимальное решение для задачи с последовательными решениями и многократными шагами. Он может использоваться для оптимизации инвестиций, управления запасами или принятия решений в условиях неопределенности.
- Стохастическое программирование: этот метод моделирования позволяет учитывать случайные факторы и неопределенность в модели. Он используется для прогнозирования и оценки рисков в экономических ситуациях, таких как финансовый рынок или климатические изменения.
- Оптимизация с помощью генетических алгоритмов: это метод моделирования, основанный на эволюционных принципах. Он используется для нахождения оптимальных решений в условиях сложных и нелинейных задач, таких как оптимизация портфеля инвестиций или планирование производства.
Каждый из этих методов имеет свои преимущества и ограничения, и выбор конкретного метода зависит от характера задачи и требуемой точности результата. Однако, используя математическое моделирование, экономисты и исследователи могут получить более точные и полные представления о сложных экономических явлениях и принять более обоснованные решения в условиях неопределенности.
Оптимизация в экономическом анализе

Экономическая оптимизация основана на математическом моделировании, которое позволяет формализовать реальные экономические процессы и применять методы математической оптимизации для нахождения наилучших решений. Важным аспектом оптимизации в экономическом анализе является учет ограничений, которые могут влиять на принимаемые решения.
Методы оптимизации в экономическом анализе могут быть различными, включая линейное и нелинейное программирование, динамическое программирование, теорию игр и другие. Целью оптимизации является нахождение такого набора решений, которое максимизирует прибыль, минимизирует затраты или достигает других заданных целей.
Примером применения оптимизации в экономическом анализе может быть оптимизация производства, где требуется определить оптимальное количество производимых товаров или оптимальное использование ресурсов для максимизации прибыли. Другим примером может быть оптимизация инвестиционного портфеля, где требуется определить оптимальное распределение активов для минимизации рисков и максимизации доходности.
Оптимизация в экономическом анализе позволяет принимать обоснованные решения на основе математических моделей и методов оптимизации. Это позволяет снизить затраты, повысить эффективность и достичь лучших результатов в экономической деятельности. Поэтому оптимизация является неотъемлемой частью современного экономического анализа и принятия решений.
Анализ экономической эффективности
Основными методами анализа экономической эффективности являются методы баланса, показателей доходности и окупаемости, а также стоимостного анализа. Каждый из этих методов имеет свои особенности и применяется в зависимости от конкретной задачи.
Метод баланса позволяет оценить экономическую эффективность путем сравнения доходов и затрат. Он позволяет определить, приносит ли проект или инвестиция положительную прибыль и является ли она достаточной для окупаемости затрат.
Методы показателей доходности и окупаемости позволяют определить, насколько быстро проект или инвестиция начинают приносить прибыль и окупают затраты. Такие показатели, как чистая приведенная стоимость (ЧПС), внутренняя норма доходности (ВНД) и срок окупаемости, позволяют оценить эффективность проекта в денежном выражении и сравнить его с другими возможными вариантами.
Стоимостный анализ позволяет определить стоимость и ценность проекта или инвестиции. Он основывается на оценке потенциальных доходов и затрат, а также стоимости ресурсов, необходимых для реализации проекта. Стоимостный анализ позволяет определить, стоит ли инвестировать в проект и какую прибыль можно ожидать от него.
Все эти методы анализа экономической эффективности позволяют принять обоснованное и обоснованное решение о том, является ли проект или инвестиция прибыльным и эффективным с точки зрения экономики. Они помогают оценить риски и возможности и выбрать наилучшее решение для достижения поставленных целей.
МетодОписаниеПримеры показателей
| Метод баланса | Сравнение доходов и затрат | Доходы, затраты, прибыль |
| Метод показателей доходности | Оценка скорости начала приносить прибыль | ЧПС, ВНД |
| Метод окупаемости | Оценка времени окупаемости затрат | Срок окупаемости |
| Стоимостной анализ | Оценка стоимости и ценности проекта | Стоимость ресурсов, потенциальные доходы и затраты |
Анализ экономической эффективности является неотъемлемой частью принятия решений в экономике. Он позволяет оценить возможности и риски, связанные с проектом или инвестицией, и выбрать наилучшее решение с точки зрения экономической эффективности.
Применение линейного программирования

Применение линейного программирования в экономических задачах позволяет оптимизировать распределение ресурсов и принимать решения, основанные на количественных данных. Этот метод применяется во многих областях экономики, включая производственную деятельность, логистику, финансы, маркетинг и другие.
Процесс решения задачи с использованием линейного программирования включает следующие шаги:
- Формулировка целевой функции, которую необходимо максимизировать или минимизировать. Целевая функция может представлять собой функцию прибыли, затраты или другой показатель эффективности.
- Определение ограничений, которые должны быть учтены при поиске оптимального решения. Ограничения могут быть связаны с ограниченными ресурсами, производственными мощностями или другими факторами.
- Построение математической модели, которая описывает задачу. Модель состоит из уравнений и неравенств, которые связывают переменные и ограничения.
- Решение математической модели с помощью алгоритмов линейного программирования. Это может быть выполнено с использованием специализированного программного обеспечения или методов ручного решения.
- Анализ полученных результатов и интерпретация оптимального решения. Полученное решение может быть использовано для принятия решений и оптимизации бизнес-процессов.
Применение линейного программирования позволяет эффективно использовать ресурсы и принимать обоснованные экономические решения. Он является мощным инструментом для моделирования и оптимизации бизнес-процессов в условиях ограниченных ресурсов и конкуренции.
Методы динамического программирования
Одной из основных идей методов динамического программирования является использование принципа оптимальности. Это означает, что наилучшее решение задачи можно получить, если известны наилучшие решения его подзадач. Таким образом, методы динамического программирования сводятся к нахождению оптимальных решений подзадач и их комбинированию для получения оптимального решения всей задачи.
Для решения задач с использованием методов динамического программирования часто используются таблицы и матрицы, которые позволяют хранить информацию о промежуточных результатах и оптимальных решениях. Это позволяет существенно сократить вычислительные затраты, так как многократно повторяющиеся подзадачи решаются один раз и результаты сохраняются для дальнейшего использования.
Применение методов динамического программирования в экономико-математических задачах позволяет учесть множество факторов и ограничений, которые могут влиять на их решение. Например, можно учитывать ресурсы, затраты, доходы, время, вероятности и другие параметры, что позволяет найти наиболее эффективные решения с точки зрения экономической эффективности.
Таким образом, методы динамического программирования являются мощным инструментом для решения экономико-математических задач. Их использование позволяет найти оптимальные решения, учитывая множество факторов и ограничений, и достичь высокой экономической эффективности.
Видео по теме:
Вопрос-ответ:
Какие экономико-математические задачи можно решить с помощью нахождения наилучшего решения с точки зрения экономической эффективности?
С помощью экономико-математического подхода можно решать множество задач, связанных с оптимизацией экономических процессов. Например, можно оптимизировать распределение ресурсов, определить оптимальное количество производимых товаров, выбрать наиболее эффективную стратегию инвестирования и многое другое.
Какие методы и модели используются для решения экономико-математических задач нахождения наилучшего решения?
Для решения таких задач могут применяться различные методы и модели, включая линейное программирование, динамическое программирование, теорию игр, архивные методы и другие. Конкретный выбор метода зависит от поставленной задачи и ее особенностей.
Какие факторы учитываются при определении наилучшего решения в экономико-математических задачах?
При определении наилучшего решения в экономико-математических задачах учитываются различные факторы, включая стоимость ресурсов, объемы производства и сбыта продукции, доходы и расходы, цены на товары, инфляцию, потребительские предпочтения и многое другое. Все эти факторы взаимодействуют и влияют на окончательное решение задачи.
Каким образом экономико-математические задачи нахождения наилучшего решения могут помочь предприятиям и организациям?
Решение экономико-математических задач нахождения наилучшего решения может помочь предприятиям и организациям в принятии обоснованных решений, связанных с оптимизацией производства, распределением ресурсов, управлением финансами и другими аспектами деятельности. Это позволяет повысить эффективность работы организаций и достичь конкурентных преимуществ на рынке.
Каковы преимущества использования экономико-математических методов в решении задач нахождения наилучшего решения?
Использование экономико-математических методов в решении задач нахождения наилучшего решения позволяет получить объективные и точные результаты, а также учесть множество факторов, которые могут оказывать влияние на решение. Это позволяет принимать обоснованные решения, основанные на математической модели, и повышать эффективность экономических процессов.
Моделирование риска и неопределенности
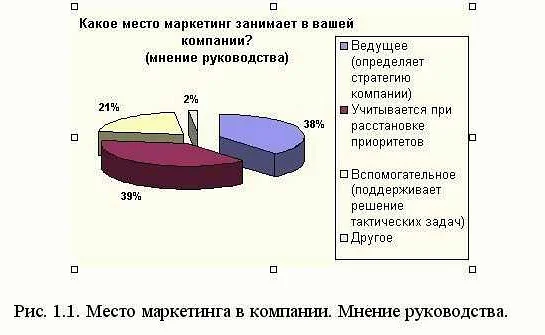
Риск и неопределенность – это неотъемлемые аспекты бизнеса. В процессе принятия решений экономисты и менеджеры сталкиваются с несколькими видами риска, такими как финансовые, рыночные, политические и технологические. Кроме того, они часто сталкиваются с ситуациями, где результаты решений не могут быть точно предсказаны.
Для того чтобы учесть риск и неопределенность, используются математические модели. Эти модели основываются на вероятностных расчетах и позволяют оценить вероятность различных исходов. При моделировании риска и неопределенности можно использовать такие методы, как статистический анализ, симуляции Монте-Карло и другие.
Одним из основных инструментов моделирования риска является анализ чувствительности. Этот метод позволяет исследовать, как изменение параметров модели влияет на результаты решения. Таким образом, можно определить, какие факторы являются наиболее рискованными и требуют особого внимания.
Моделирование риска и неопределенности позволяет принимать более обоснованные решения, учитывая возможные негативные последствия и вероятность их возникновения. Это помогает снизить риски и повысить экономическую эффективность деятельности компании или организации.
Выводы:
- Моделирование риска и неопределенности является важным инструментом в экономико-математических задачах.
- Риск и неопределенность – неотъемлемые аспекты бизнеса, которые нужно учитывать при принятии решений.
- Математические модели позволяют оценить вероятность различных исходов и учесть риск и неопределенность.
- Анализ чувствительности помогает определить наиболее рискованные факторы и принять обоснованные решения.
- Моделирование риска и неопределенности помогает снизить риски и повысить экономическую эффективность.
Многокритериальная оптимизация
Основная цель многокритериальной оптимизации заключается в поиске такого решения, которое будет наилучшим с точки зрения всех учитываемых критериев. При этом каждый критерий может иметь свою важность и вес в общей оценке решения.
Для решения задачи многокритериальной оптимизации применяются различные методы и алгоритмы, такие как метод векторной оптимизации, метод главных компонент, метод анализа иерархий и другие. Основная идея состоит в нахождении компромиссного решения, которое удовлетворяет требованиям всех критериев.
Важным этапом в многокритериальной оптимизации является формулировка критериев и их взаимодействия. Необходимо определить, какие критерии являются наиболее важными и как они влияют друг на друга. Затем проводится анализ и оценка каждого критерия в отдельности, а затем совместная оценка.
Многокритериальная оптимизация активно применяется в различных сферах экономики, таких как финансы, производство, логистика, маркетинг и другие. Примерами задач, которые можно решить с помощью многокритериальной оптимизации, являются оптимизация портфеля инвестиций, выбор поставщика товаров, планирование производства.
В результате применения методов многокритериальной оптимизации можно получить оптимальное решение, которое удовлетворяет всем поставленным требованиям. Это позволяет повысить эффективность принимаемых решений и достичь лучших результатов в различных сферах экономики.


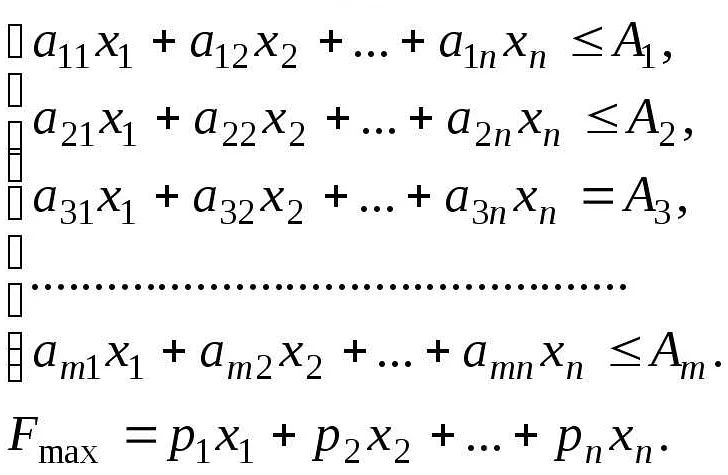

Статья очень интересная и актуальная. Я всегда задумывался, каким образом экономические решения могут быть оптимизированы с помощью математических моделей. Подход, описанный в статье, позволяет учесть различные факторы и оценить экономическую эффективность различных вариантов решения. Это особенно полезно в условиях неопределенности и ограниченных ресурсов. Мне понравилось, как автор объяснил принципы принятия экономических решений с помощью линейного программирования. Это метод, с которым я не знаком, но теперь я понял, как он может быть применен для оптимизации процессов в экономике. Также интересно, что автор упомянул и другие подходы, такие как показатели эффективности и мультикритериальный анализ. Это дает возможность выбрать наиболее подходящий метод, в зависимости от задачи и имеющихся данных. Я бы хотел увидеть больше примеров и практических советов по применению этих методов. Например, как использовать экономико-математические модели для оптимизации распределения ресурсов или выбора оптимального пути развития компании. Также было бы интересно узнать о возможных ограничениях и проблемах, связанных с применением этих методов. В целом, статья вызвала у меня большой интерес и побудила задуматься над новыми возможностями применения математики в экономике. Я с нетерпением жду продолжения и надеюсь, что автор расскажет больше о практическом применении этих методов в реальных ситуациях.
Эта статья очень интересна и полезна для тех, кто интересуется экономико-математическими задачами и их решением с точки зрения экономической эффективности. Я всегда задаюсь вопросом, как найти наилучшее решение в экономической сфере, чтобы добиться максимальной прибыли или снижения затрат. Математика, безусловно, играет важную роль в экономике, позволяя анализировать и моделировать различные экономические процессы. Она помогает найти оптимальные решения на основе данных и предсказаний. Особенно интересно узнать о различных методах решения задач, таких как линейное программирование, теория игр и динамическое программирование. Каждый из них имеет свои преимущества и применение в различных ситуациях. Я убеждаюсь в том, что использование экономико-математических методов и алгоритмов может привести к оптимизации бизнес-процессов и повышению эффективности деятельности компании. Такие решения помогут выделиться на фоне конкурентов и достичь успеха на рынке. Спасибо автору за полезную информацию и надеюсь, что он продолжит делиться своими знаниями и опытом в этой области. Я с нетерпением жду новых статей на эту тему!