Что такое пф в математике

Предел функции в математике — это концепция, позволяющая определить, как функция приближается к определенному значению при стремлении ее аргумента к определенной точке. Предел функции является основным инструментом анализа и играет важную роль в изучении непрерывности, производных и интегралов. Узнайте, как определить предел функции и применить эту концепцию для решения математических задач.

ПФ (пользовательская функция) в математике — это абстрактный объект, который принимает одно или более значения и возвращает результат на основе заданного алгоритма. Она является основным строительным блоком для создания программ, решающих различные задачи математического характера.

Одним из примеров ПФ является функция сложения двух чисел. Входными значениями для этой функции являются два числа, а результатом является их сумма. Это простой и понятный пример, который помогает понять, как работает пользовательская функция в математике.

ПФ широко применяются в математике для решения различных задач. Они могут использоваться для выполнения математических операций, решения уравнений, построения графиков и т.д. Пользовательские функции позволяют упростить и структурировать математические вычисления, делая их более понятными и эффективными.

Таким образом, пользовательская функция является важным инструментом в математике, который позволяет создавать программы для решения различных задач. Они помогают упростить и автоматизировать математические операции, что делает процесс вычислений более эффективным и удобным.

Понятие пф в математике

Понятие пф в математике относится к теории вероятностей и используется для описания вероятности наступления события.

Пф, сокращение от «плотность функции», представляет собой математическую функцию, которая описывает распределение вероятностей случайной величины. Плотность вероятности позволяет определить, с какой вероятностью случайная величина примет определенное значение в заданном интервале.

Примеры плотности вероятности включают гауссово (нормальное) распределение, равномерное распределение и экспоненциальное распределение.

Плотность вероятности широко применяется в статистике, физике, экономике и других областях, где необходимо анализировать случайные процессы и предсказывать их вероятность.

Видео по теме:

Значение пф в математике

Производные функций являются важным инструментом в математическом анализе и используются во многих областях, включая физику, экономику, статистику и инженерные науки. Они позволяют решать задачи оптимизации, находить экстремумы функций, исследовать поведение функций в различных точках и т. д.

Пример:

Рассмотрим функцию f(x) = x^2. Ее производная функция обозначается как f'(x) или df/dx. Найдем производную функции f'(x):

f'(x) = lim

h->0

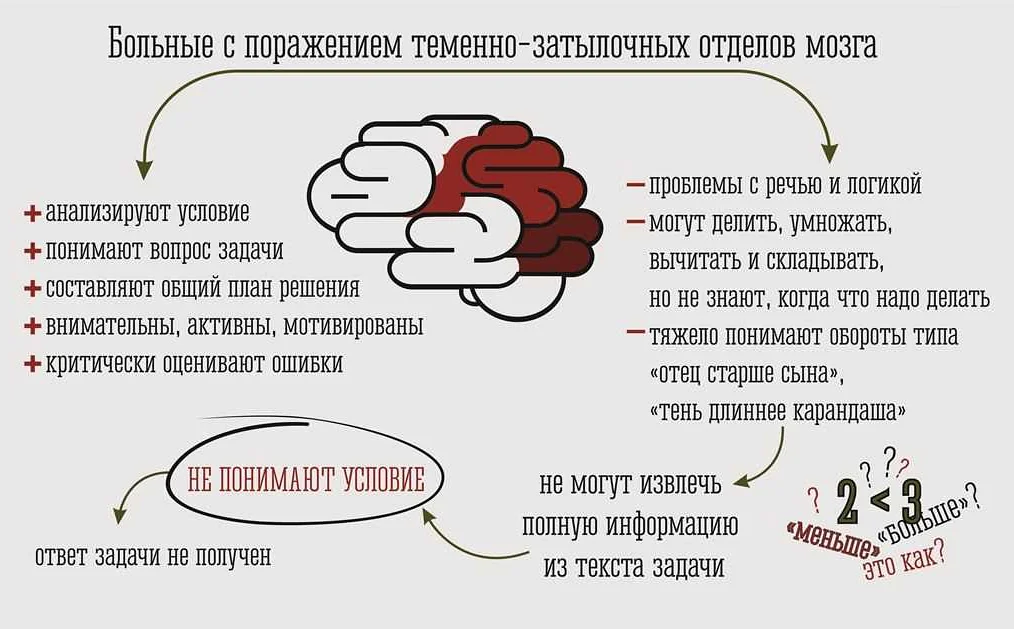
(f(x+h) — f(x))/h

Подставляя значения функции и беря предел при h->0, получим:

f'(x) = lim

h->0

((x+h)^2 — x^2)/h

f'(x) = lim

h->0

(x^2 + 2xh + h^2 — x^2)/h

f'(x) = lim

h->0

(2xh + h^2)/h

f'(x) = lim

h->0

2x + h = 2x

Таким образом, производная функции f(x) = x^2 равна f'(x) = 2x. Это означает, что скорость изменения функции f(x) = x^2 в каждой точке равна удвоенному значению этой точки.

Примеры пф в математике

Префиксная форма (пф) может использоваться для представления математических выражений и формул. Вот несколько примеров пф в математике:

1. Пример пф для арифметического выражения:

Пф: + 2 3

Обычная форма: 2 + 3

2. Пример пф для логического выражения:

Пф: AND TRUE FALSE

Обычная форма: TRUE AND FALSE

3. Пример пф для математической формулы:

Пф: sqrt + 25 * 3 7

Обычная форма: sqrt(25 + (3 * 7))

Префиксная форма позволяет упростить выполнение математических операций и вычисление выражений с использованием компьютерных программ и алгоритмов. Она часто используется в функциональных языках программирования, таких как Lisp.

Применение пф в математике

Применение пф в математике может быть разнообразным:

1. Вычисление количества перестановок элементов. Например, если у нас есть множество из n элементов, то количество различных перестановок этих элементов будет равно n!. Это важно при решении задач, связанных с размещением объектов или составлением различных комбинаций.
2. Определение вероятности различных исходов. ПФ может быть использовано для определения вероятности того, что определенное событие произойдет в определенной последовательности. Например, при подбрасывании монеты вероятность выпадения герба или решки будет равна 1/2, так как есть два равновероятных исхода.
3. Анализ комбинаторных задач. ПФ позволяет решать задачи на подсчет количества различных объектов, учитывая их упорядоченность и возможность перестановки. Например, при расстановке различных предметов на полке или витрине, мы можем использовать ПФ для вычисления количества возможных вариантов.
4. Расчет числа различных комбинаций и вариаций. ПФ позволяет вычислить количество различных комбинаций и вариаций элементов множества. Например, при составлении паролей или выборе лотерейных номеров, мы можем использовать ПФ для определения количества возможных вариантов.

Применение пф в математике имеет широкий спектр и находит применение в различных областях, таких как комбинаторика, теория вероятностей, статистика и дискретная математика. Правило Перестановок Факториала является одним из базовых понятий в этих областях и позволяет решать множество задач, связанных с перестановками и комбинаторикой.

Роль пф в математических расчетах

Одна из основных областей, где применяется пф, — это комбинаторика. Полный факториал используется для нахождения количества возможных перестановок, размещений и сочетаний элементов. Например, для определения числа перестановок из n элементов можно использовать формулу n!. Это позволяет рассчитать сколько различных порядков можно получить из заданного набора элементов.

Пф также используется в теории вероятности и статистике. Например, для определения количества различных исходов при выборе элементов из заданного множества или для вычисления вероятности событий.

Кроме того, полный факториал может быть использован для решения задач в математическом анализе, теории чисел и других областях математики. Он является важным инструментом для проведения различных расчетов и упрощения математических выражений.

Влияние пф на решение математических задач

Влияние пф на решение математических задач не может быть переоценено, поскольку он позволяет строить доказательства пошагово, начиная с базового случая и затем переходя к общему случаю. Этот метод доказательства позволяет установить утверждения для всех натуральных чисел, необходимых для решения задачи.

Пф также позволяет выявить закономерности и установить связи между различными математическими объектами. Он широко применяется в различных областях математики, включая алгебру, теорию чисел, комбинаторику и другие.

Применение пф требует логического мышления и умения проводить строгие математические рассуждения. Это позволяет развить навыки анализа, решения проблем и углубить понимание математических концепций.

В целом, пф играет важную роль в решении математических задач, помогая установить и доказать свойства и закономерности для всех натуральных чисел. Он является одним из фундаментальных инструментов, используемых в математике, и его понимание и применение существенно облегчают решение сложных задач.

Пф и компьютерные программы

В компьютерных программах пф используется для решения задач, связанных с алгоритмами и вычислениями. Она позволяет представить сложные математические выражения в более простой и удобной форме, что упрощает их реализацию в коде программы.

Программисты могут использовать пф для упрощения вычислений, оптимизации кода, а также для решения задач, связанных с моделированием и анализом данных. Пф позволяет представлять математические функции и операции в виде полиномов, что упрощает их использование в программировании.

Например, пф может быть использована для представления линейных и квадратичных функций, что позволяет производить с ними различные операции, такие как сложение, вычитание, умножение и деление. Также пф может быть использована для аппроксимации сложных функций с помощью полиномов, что позволяет упростить вычисления и сократить время работы программы.

Таким образом, пф является важным инструментом в компьютерных программировании, который позволяет упростить вычисления и решение математических задач.

Пф в математическом образовании

При изучении математики в школе и вузе учащиеся сталкиваются с различными типами доказательств, такими как доказательства по индукции, доказательства от противного, доказательства с помощью прямого вывода и многие другие. Эти доказательства помогают учащимся понять и запомнить основные понятия и теоремы, а также развить навыки логического мышления и анализа.

Пф также играет важную роль в научной деятельности и исследованиях в области математики. Ученые и математики используют доказательства для подтверждения своих теорий и открытий, а также для развития новых математических концепций и теорий. Доказательства играют особенно важную роль в таких областях математики, как алгебра, геометрия, математический анализ и теория вероятностей.

Изучение и применение пф в математическом образовании помогает учащимся развить навыки анализа, решения проблем и логического мышления, которые могут быть полезными не только в математике, но и в других областях жизни. Поэтому пф является важной составляющей образования и развития учащихся.

Вопрос-ответ:

Что такое пф в математике?

Пф в математике означает «поле факторов» и представляет собой алгебраическое расширение поля, полученное путем добавления к исходному полю новых элементов, называемых факторами.

Каким образом можно получить поле факторов?

Поле факторов можно получить путем деления множества всех многочленов на множество всех многочленов с неприводимыми коэффициентами.

Какие примеры использования полей факторов в математике?

Поля факторов широко используются в алгебре и геометрии. Например, они применяются для решения уравнений, построения расширенных числовых систем, а также для изучения геометрических объектов, таких как конические секции и эллиптические кривые.

Какие свойства имеют поля факторов?

Поля факторов обладают рядом важных свойств. Например, они являются коммутативными кольцами, имеют ассоциативность и дистрибутивность умножения относительно сложения. Кроме того, поля факторов являются полем, то есть в них определены все операции: сложение, умножение, вычитание и деление.

Какие применения имеют поля факторов в криптографии?

Поля факторов используются в криптографии для создания криптографических систем, таких как алгоритм RSA. В этих системах поля факторов обеспечивают безопасное шифрование и дешифрование данных, а также генерацию ключевых пар для защиты информации.