Что такое площадь и периметр в математике 4 класс
Содержимое
- 1 Что такое площадь и периметр в математике 4 класс
Площадь и периметр — это понятия, связанные с геометрией и математикой. В этой статье мы рассмотрим, что такое площадь и периметр, как они вычисляются, и как они применяются в математике для 4-го класса. Узнайте, как решать задачи на вычисление площади и периметра различных фигур и какие формулы использовать.
В математике 4 класса ученики начинают изучать понятия площади и периметра. Площадь — это количество площади, занимаемой фигурой, а периметр — это сумма длин всех сторон фигуры. Эти понятия важны, когда мы хотим измерить размеры и формы различных объектов.
Площадь и периметр помогают нам понять, сколько площади занимает фигура и какие размеры нужны для построения ограды или покрытия. Например, если у нас есть квадрат со стороной 4 см, его площадь будет равна 16 квадратным сантиметрам, а периметр — 16 сантиметрам.
Для вычисления площади и периметра различных фигур мы используем формулы. Например, для прямоугольника площадь вычисляется как произведение длины и ширины, а периметр — удвоенная сумма длины и ширины. Примеры с различными фигурами помогут ученикам лучше понять эти понятия и научиться использовать формулы для расчетов.
Например, у нас есть треугольник со сторонами 5 см, 8 см и 10 см. Чтобы найти периметр, нужно сложить длины всех сторон: 5 + 8 + 10 = 23 см. Площадь треугольника можно вычислить, используя формулу Герона: S = √p(p — a)(p — b)(p — c), где p — полупериметр, а a, b и c — длины сторон треугольника. В этом случае, p = (5 + 8 + 10) / 2 = 11.5. Подставляем значения и получаем: S = √11.5(11.5 — 5)(11.5 — 8)(11.5 — 10) ≈ 20.39 квадратных сантиметров.
Изучение площади и периметра в математике 4 класса является важным шагом в развитии понимания геометрии. Эти концепции помогают ученикам развить навыки измерения, анализа и расчетов, которые могут быть применены в реальной жизни.
Что такое площадь в математике 4 класс: объяснение и примеры

Чтобы найти площадь прямоугольника, нужно перемножить длину одной его стороны на длину другой стороны. Например, если одна сторона прямоугольника равна 5 единицам, а другая сторона – 3 единицы, то его площадь будет равна 5 × 3 = 15 квадратным единицам.
У квадрата все стороны равны друг другу, поэтому для нахождения его площади нужно возвести длину одной стороны в квадрат. Например, если сторона квадрата равна 4 единицам, то его площадь будет равна 4 × 4 = 16 квадратным единицам.
Для нахождения площади прямоугольного треугольника нужно умножить длину одного его катета на длину другого катета и разделить полученный результат на 2. Например, если длина одного катета равна 3 единицам, а длина другого катета – 4 единицам, то площадь треугольника будет равна (3 × 4) / 2 = 6 квадратным единицам.
Таким образом, площадь – это важное понятие в математике, которое помогает измерять поверхности различных фигур и решать задачи, связанные с размерами и площадью. Зная различные формулы для нахождения площади различных фигур, можно успешно решать задачи и проводить измерения.
Определение площади
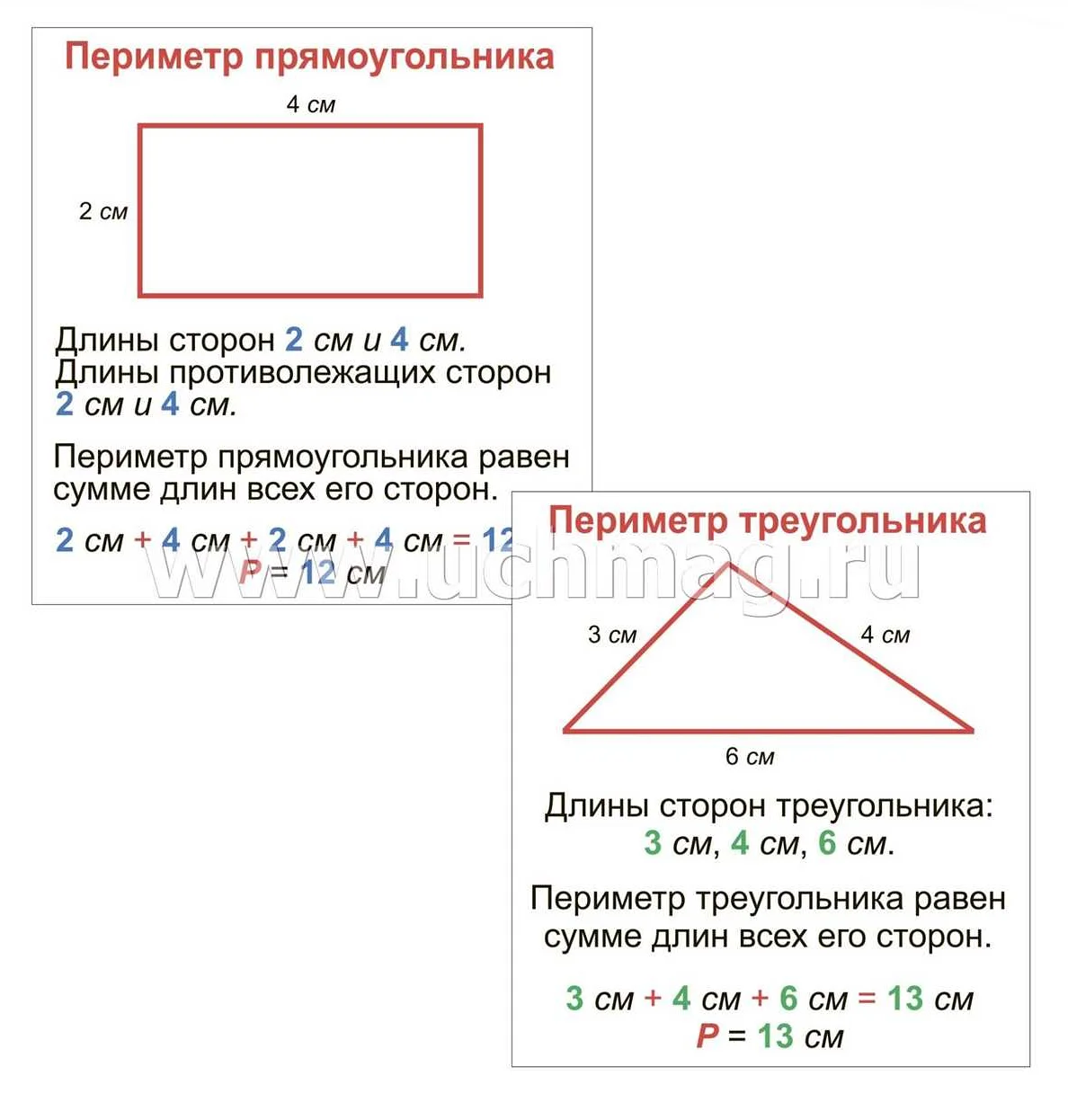
Площадь измеряется в квадратных единицах, например, квадратных сантиметрах (см2), квадратных метрах (м2), квадратных километрах (км2) и т.д.
Для различных плоских фигур существуют формулы для вычисления площади. Например, для прямоугольника площадь вычисляется по формуле:
| Площадь прямоугольника: | П = а * b, |
| где а и b – длины сторон прямоугольника. |
Также существуют формулы для вычисления площади других фигур, например, квадрата, треугольника и т.д.
Площадь позволяет нам определить, сколько единиц площади занимает данная фигура на плоскости. Зная площадь, мы можем сравнивать фигуры по их размеру или находить площадь новых фигур, полученных путем разделения или объединения других фигур.
Формула для расчета площади

Например, для расчета площади прямоугольника применяется простая формула:
- Площадь прямоугольника = длина × ширина
Для расчета площади квадрата применяется та же формула:
- Площадь квадрата = сторона × сторона
Для расчета площади треугольника используется следующая формула:
- Площадь треугольника = (основание × высота) / 2
Для расчета площади круга используется формула:
- Площадь круга = π × радиус^2
Где π (пи) – это математическая константа, приближенное значение которой равно 3,14.
Зная формулы для расчета площади различных фигур, можно легко определить их площадь, зная значения соответствующих параметров.
Примеры расчета площади
Для понимания площади и ее расчета, рассмотрим несколько примеров:
Пример 1:
У нас есть прямоугольник со сторонами 5 см и 7 см. Чтобы найти площадь этого прямоугольника, нужно умножить длину на ширину: 5 см * 7 см = 35 см². Таким образом, площадь прямоугольника составляет 35 квадратных сантиметров.
Пример 2:
Допустим, у нас есть квадрат со стороной 9 м. Чтобы найти площадь этого квадрата, нужно возвести сторону в квадрат: 9 м * 9 м = 81 м². Таким образом, площадь квадрата составляет 81 квадратный метр.
Пример 3:
Рассмотрим треугольник с основанием 12 см и высотой 8 см. Чтобы найти площадь треугольника, нужно умножить половину основания на высоту: (1/2) * 12 см * 8 см = 48 см². Таким образом, площадь треугольника составляет 48 квадратных сантиметров.
Примечание: Площадь измеряется в квадратных единицах, таких как квадратные сантиметры (см²) или квадратные метры (м²).
Площадь прямоугольника
Чтобы найти площадь прямоугольника, нужно умножить длину одной из его сторон на длину другой стороны.
Формула для нахождения площади прямоугольника выглядит так: S = a * b, где S — площадь, а и b — длины сторон прямоугольника.
Например, у нас есть прямоугольник со сторонами 5 и 9. Чтобы найти его площадь, нужно умножить 5 на 9: S = 5 * 9 = 45.
Таким образом, площадь этого прямоугольника равна 45 квадратным единицам.
Площадь прямоугольника можно наглядно представить с помощью таблицы. Ниже приведена таблица,
в которой каждая ячейка соответствует одной квадратной единице площади прямоугольника.
Площадь треугольника
Формула для расчета площади треугольника зависит от вида треугольника:
1. Для прямоугольного треугольника площадь можно найти по формуле: площадь = (основание * высота) / 2, где основание — это одна из сторон треугольника, а высота — перпендикуляр, опущенный из вершины треугольника на основание.
2. Для равнобедренного треугольника площадь можно найти по формуле: площадь = (основание * высота) / 2, где основание — это одна из сторон треугольника, а высота — перпендикуляр, опущенный из вершины треугольника на основание.
3. Для произвольного треугольника площадь можно найти по формуле Герона: площадь = √(p * (p — a) * (p — b) * (p — c)), где p — полупериметр треугольника, а a, b и c — длины его сторон.
Для вычисления площади треугольника необходимо знать длины его сторон и другие характеристики, такие как высота или полупериметр.
Пример:
Пусть дан треугольник со сторонами a = 5, b = 7 и c = 8.
Для такого треугольника можно вычислить его полупериметр: p = (a + b + c) / 2 = (5 + 7 + 8) / 2 = 10.
Затем можно использовать формулу Герона: площадь = √(p * (p — a) * (p — b) * (p — c)) = √(10 * (10 — 5) * (10 — 7) * (10 — 8)) = √(10 * 5 * 3 * 2) = √300 = 17.32.
Таким образом, площадь треугольника со сторонами 5, 7 и 8 равна 17.32.
Площадь квадрата

Для вычисления площади квадрата необходимо знать длину его стороны. Площадь квадрата можно найти, умножив длину стороны на саму себя, то есть возвести ее в квадрат.
Формула для вычисления площади квадрата: S = a^2, где S — площадь квадрата, а — длина стороны.
Например, если сторона квадрата равна 5 единицам, то площадь будет равна 5 * 5 = 25 квадратных единиц.
Таким образом, площадь квадрата позволяет определить, сколько квадратных единиц занимает эта фигура.
Площадь круга
Формула для вычисления площади круга:
- S = π * r^2
где π — математическая константа, примерное значение которой равно 3.14, а r — радиус круга.
Для вычисления площади круга нужно знать значение радиуса и подставить его в формулу. Затем произвести вычисления.
Пример:
- Пусть радиус круга равен 5 см.
- Подставим значение радиуса в формулу:
- S = 3.14 * 5^2
- S = 3.14 * 25
- S ≈ 78.5
- Площадь круга равна примерно 78.5 квадратных сантиметров.
Таким образом, площадь круга можно вычислить, зная его радиус и используя формулу S = π * r^2.
Видео по теме:
Что такое площадь?
Площадь — это мера площади поверхности фигуры. Она измеряется в квадратных единицах (например, квадратных сантиметрах или квадратных метрах) и показывает, сколько места занимает фигура на плоскости.
Как посчитать площадь прямоугольника?
Чтобы посчитать площадь прямоугольника, нужно умножить длину одной стороны на длину другой стороны.
Как посчитать площадь треугольника?
Чтобы посчитать площадь треугольника, нужно умножить длину основания на высоту и разделить полученное значение на 2.
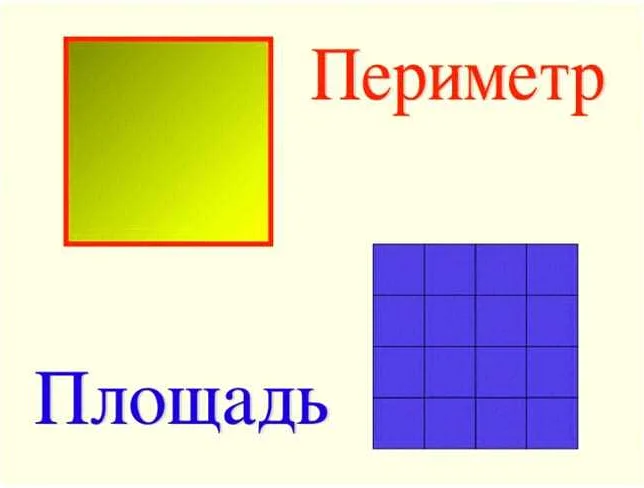
Что такое периметр?
Периметр — это сумма длин всех сторон фигуры. Он измеряется в единицах длины (например, сантиметрах или метрах) и показывает, сколько всего пути нужно пройти по контуру фигуры.
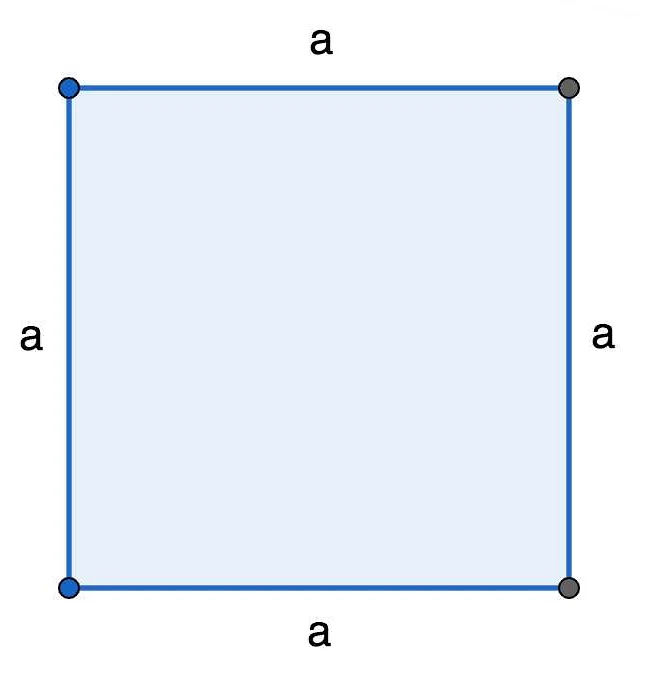
Как посчитать периметр квадрата?
Чтобы посчитать периметр квадрата, нужно умножить длину одной стороны на 4.
Как определить площадь фигуры?
Площадь фигуры определяется как количество квадратных единиц, которые можно поместить внутри этой фигуры. Для простых фигур, таких как прямоугольник или квадрат, площадь вычисляется как произведение длины и ширины. Для сложных фигур, таких как треугольник или окружность, существуют специальные формулы для вычисления площади.


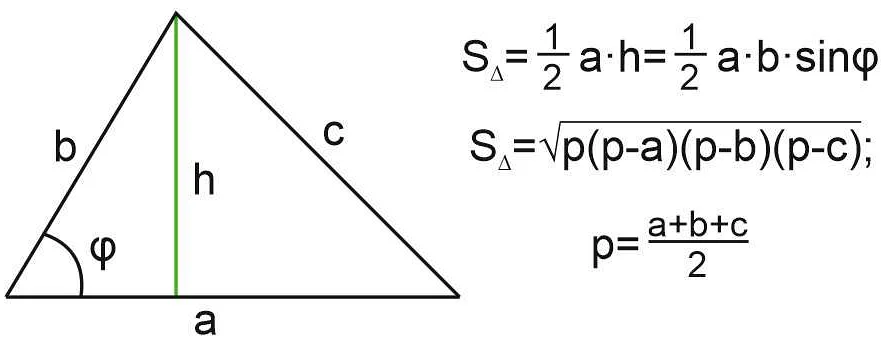
Статья очень понятно и доступно объясняет понятия площади и периметра в математике для 4 класса. Я как родитель четвероклассника, всегда стараюсь помочь своему ребенку в изучении новых материалов, и эта статья очень пригодилась. Автор дал простое и ясное определение площади и периметра, а также привел примеры, что позволяет усвоить материал гораздо легче. Мне особенно понравилось, как автор использовал наглядные схемы и картинки, чтобы проиллюстрировать тему. Это очень помогает детям визуализировать и запомнить материал. Мой ребенок смог легко понять, что такое площадь и периметр и даже решил несколько задач самостоятельно. Я очень доволен и благодарен автору за такую полезную и понятную статью. Надеюсь, что автор продолжит делиться с нами своими знаниями и опытом в будущем.