Что такое равная фигура в математике

Равная фигура в математике — это геометрическая фигура, у которой все стороны или углы равны друг другу. Узнайте больше о свойствах равных фигур и их применении в математике.

Равная фигура в математике — это геометрическая фигура, которая имеет равные размеры и равную форму с другой фигурой. Она может быть симметричной относительно некоторой оси или центра, а также может поворачиваться, переноситься или отражаться без изменения своих размеров и формы.

Определение равной фигуры дает возможность сравнивать и классифицировать геометрические объекты, а также решать разнообразные задачи в математике и физике. Свойства равных фигур включают равенство длин сторон, равенство углов, равенство площадей и объемов.

Например, два треугольника с равными длинами сторон и равными углами считаются равными фигурами. Это означает, что один треугольник может быть превращен в другой путем поворота, переноса или отражения без изменения его размеров и формы.

Равные фигуры имеют важное значение во многих областях математики, включая геометрию, топологию, алгебру и физику. Они помогают упрощать и анализировать сложные задачи, подтверждают симметричные и геометрические соотношения, а также служат основой для изучения преобразований и симметрий фигур.

Определение равной фигуры в математике

Для того чтобы две фигуры считались равными, они должны удовлетворять определенным условиям. Во-первых, соответствующие стороны и углы двух фигур должны быть равными. Во-вторых, фигуры должны иметь одинаковую форму. Например, два треугольника считаются равными, если у них равны соответствующие стороны и углы, и их формы совпадают.

Равная фигура — важное понятие в математике, так как оно позволяет сравнивать и классифицировать различные геометрические фигуры. С помощью понятия равной фигуры можно доказывать различные свойства и теоремы, а также решать различные задачи в геометрии.

Свойства равных фигур

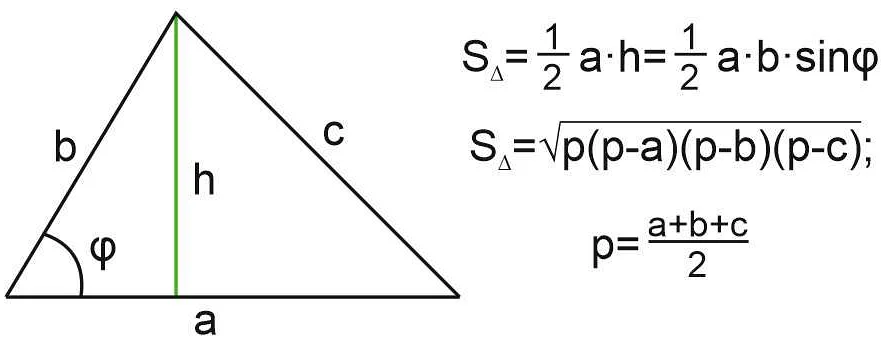
Равные фигуры имеют ряд особенностей и свойств, которые позволяют сравнивать их между собой и делать выводы о их равенстве:

1. Равные фигуры имеют одинаковую форму и размеры. Это значит, что все их стороны и углы совпадают.

2. Равные фигуры могут быть смещены, повернуты или отражены без изменения своей формы и размеров. Например, если две фигуры можно наложить друг на друга так, чтобы они полностью совпали, то они равны.

3. Если две фигуры равны, то все их характеристики также равны. Например, если у двух треугольников равны все стороны и углы, то они равны в целом.

4. Равные фигуры могут быть различной ориентации и расположении в пространстве, но при этом сохраняют свою равность.

5. Если две фигуры состоят из одних и тех же элементов, расположенных в одинаковом порядке, то они равны. Например, два равных треугольника могут быть собраны из одних и тех же сторон и углов.

6. Равные фигуры можно разделить на равные части с помощью параллельных линий или плоскостей.

7. Равные фигуры обладают равной площадью и периметром, а также равными другими характеристиками, такими как длина диагонали или радиус окружности, вписанной или описанной в фигуру.

8. Равные фигуры могут быть использованы для доказательства равенства других фигур. Например, если два треугольника равны, то можно сделать вывод о равенстве сторон или углов в других фигурах, построенных на основе этих треугольников.

Использование этих свойств равных фигур позволяет решать различные задачи в геометрии, а также делать выводы о равенстве и подобии различных фигур.

Равные фигуры и их характеристики

Важной характеристикой равных фигур является их равенство площадей. Если две фигуры совпадают, то их площади также будут одинаковыми. Это свойство является основным признаком равенства фигур и позволяет сравнивать их.

Еще одной важной характеристикой равных фигур является равенство всех соответствующих углов и сторон. Если две фигуры равны, то их углы и стороны будут иметь одинаковые значения. Это свойство позволяет устанавливать равенство фигур без измерения их площадей.

Примеры равных фигур:

Равные треугольники:	Равные прямоугольники:	Равные окружности:

В приведенной таблице показаны примеры равных фигур. Обратите внимание, что все фигуры совпадают по форме и размерам, что позволяет считать их равными.

Примеры равных фигур

В математике существует множество примеров равных фигур, которые могут быть разных форм и размеров. Некоторые из них включают:

1. Равные треугольники: Два треугольника называются равными, если у них равны все стороны и все углы. Например, треугольник ABC и треугольник DEF будут равными, если AB = DE, BC = EF и углы ABC и DEF равны.

2. Равные окружности: Две окружности считаются равными, если их радиусы равны. Например, окружность с радиусом 5 и окружность с радиусом 5 также будут равными.

3. Равные прямоугольники: Два прямоугольника называются равными, если их стороны и углы соответственно равны. Например, прямоугольник с длиной 4 и шириной 6 будет равным прямоугольнику с длиной 6 и шириной 4.

4. Равные квадраты: Два квадрата считаются равными, если их стороны равны. Например, квадрат со стороной 3 и квадрат со стороной 3 также будут равными.

Это лишь некоторые примеры равных фигур. В математике существует множество других примеров, которые можно исследовать и изучать.

Как доказать равенство фигур

Существует несколько способов доказать, что две фигуры равны:

1. Доказательство по определению. Если две фигуры имеют одинаковую форму и размеры, то они считаются равными по определению. Для этого необходимо сравнить соответствующие стороны, углы и другие элементы фигур.
2. Доказательство с использованием свойств равенства. В математике существуют свойства, которые позволяют доказать равенство фигур. Например, свойство равных сторон треугольников или свойство равных углов параллельных прямых.
3. Доказательство посредством конструкции. Иногда равенство фигур можно доказать, построив дополнительные элементы или проведя определенные конструкции. Например, можно провести медиану или биссектрису и доказать, что они имеют одинаковую длину.

Важно отметить, что доказательство равенства фигур должно быть строго и логично. Для этого необходимо использовать аксиомы и правила вывода, которые являются основой математической логики.

В заключение, доказательство равенства фигур — это процесс, который позволяет установить, что две фигуры имеют одинаковую форму и размеры. Оно является важной частью геометрии и требует использования различных методов и свойств.

Применение равных фигур в реальной жизни

Одним из примеров применения равных фигур является строительство. При построении зданий и сооружений инженеры и архитекторы используют равные фигуры для обеспечения симметрии и стабильности конструкции. Например, при строительстве мостов используются равные треугольники, которые обеспечивают равномерное распределение нагрузки и повышают прочность сооружения.

Еще одним примером применения равных фигур является дизайн и создание одежды. При пошиве одежды дизайнеры используют равные фигуры, такие как круги, прямоугольники и треугольники, для создания симметричных и гармоничных моделей. Равные фигуры помогают добиться правильной пропорции и сбалансированного вида одежды.

Кроме того, равные фигуры находят применение в дизайне интерьера. Декораторы и дизайнеры используют равные фигуры для создания симметрии и гармонии в помещении. Например, равные квадраты или круги могут быть использованы для создания узоров на стенах или полах, что придает комнате эстетическую привлекательность и уют.

В искусстве также применяются равные фигуры. Художники используют равные фигуры для создания гармоничных композиций и баланса в своих произведениях. Например, равные прямоугольники или круги могут быть использованы для разделения холста на несколько частей или для создания повторяющихся узоров.

Область примененияПримеры

Строительство	Мосты, здания
Мода и дизайн одежды	Симметричные модели, узоры
Дизайн интерьера	Узоры на стенах и полах
Искусство	Композиции на холсте

Вопрос-ответ:

Что такое равная фигура?

Равная фигура — это геометрическая фигура, которая имеет одинаковую форму и размеры с другой фигурой.

Как можно определить равность двух фигур?

Две фигуры считаются равными, если они имеют одинаковую форму и размеры, то есть все соответствующие стороны и углы равны.

Какие свойства у равных фигур?

У равных фигур есть несколько свойств: все соответствующие стороны и углы равны, они имеют одинаковую форму и размеры, а также равные площади и периметры.

Можно ли найти примеры равных фигур?

Да, можно найти множество примеров равных фигур. Например, два равнобедренных треугольника с одинаковой длиной основания и равными углами при основании являются равными фигурами.

Какое значение имеет понятие равной фигуры в математике?

Понятие равной фигуры в математике является основным для сравнения геометрических объектов. Оно позволяет определить, когда две фигуры совпадают, и использовать это знание для решения различных задач и построений.

Что такое равная фигура в математике?

Равная фигура в математике — это фигура, которая может быть совмещена с другой фигурой путем поворота, переноса или зеркального отражения. Другими словами, равные фигуры имеют одинаковую форму и размеры.

Равные фигуры и их роль в геометрии

В геометрии равные фигуры играют важную роль при решении задач и построении различных доказательств. Благодаря свойству равенства, мы можем использовать равные фигуры для проверки равенства двух геометрических объектов или для построения новых фигур, основываясь на уже известных.

Один из способов доказательства равенства двух фигур — это доказательство с помощью равных треугольников. Если мы можем найти такие треугольники, которые имеют одинаковые стороны и углы, то мы можем утверждать, что соответствующие части двух фигур равны. Это свойство равных фигур позволяет нам решать задачи на равенство сторон и углов, а также проводить доказательства с использованием треугольников.

Также равные фигуры позволяют нам строить новые фигуры с помощью уже известных. Например, если у нас есть равные треугольники, мы можем построить равнобедренный треугольник, проведя медиану из вершины до основания. Это свойство равных фигур позволяет нам создавать различные фигуры с заданными параметрами, используя уже известные и проверенные конструкции.

Таким образом, равные фигуры являются важным инструментом в геометрии. Они помогают нам анализировать и понимать свойства и отношения геометрических объектов, решать задачи и строить новые фигуры. Понимание равных фигур позволяет нам глубже погрузиться в мир геометрии и применять ее в различных областях науки и практической деятельности.

Видео по теме: